Binary Trees Traversal
Basic Traversal
- 94. Binary Tree Inorder Traversal
- 144. Binary Tree Preorder Traversal
- 145. Binary Tree Postorder Traversal
DFS (Depth First Searchs,深度优先遍历)
Preorder Traversal(前序遍历)
二叉树先序遍历的实现思想是:
- 访问根节点;
- 访问当前节点的左子树;
- 若当前节点无左子树,则访问当前节点的右子树;
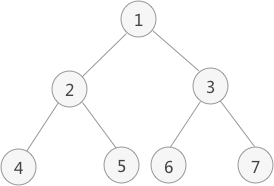
以上图为例,采用先序遍历的思想遍历该二叉树的过程为:
- 访问该二叉树的根节点,找到 1;
- 访问节点 1 的左子树,找到节点 2;
- 访问节点 2 的左子树,找到节点 4;
- 由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树,因此现在开始遍历,即访问节点 5;
- 由于节点 5 无左右子树,因此节点 5 遍历完成,并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ,并开始遍历该节点的右子树,即访问节点 3;
- 访问节点 3 左子树,找到节点 6;
- 由于节点 6 无左右子树,因此节点 6 遍历完成,回到节点 3 并遍历其右子树,找到节点 7;
- 节点 7 无左右子树,因此以节点 3 为根节点的子树遍历完成,同时回归节点 1。由于节点 1 的左右子树全部遍历完成,因此整个二叉树遍历完成;
因此,上图中二叉树采用先序遍历得到的序列为:
1 2 4 5 3 6 7
Recursion
def preorder(root):
if not root:
return
print(root.val)
preorder(root.left)
preorder(root.right)
Iterative (Without recursion)
- use stack
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
cur = root
while cur or stack:
if cur:
res.append(cur.val)
stack.append(cur.right)
cur = cur.left
else:
cur = stack.pop()
return res
Inorder Traversal(中序遍历)
二叉树中序遍历的实现思想是:
- 访问当前节点的左子树;
- 访问根节点;
- 访问当前节点的右子树;
例子

以上图为例,采用中序遍历的思想遍历该二叉树的过程为:
- 访问该二叉树的根节点,找到 1;
- 遍历节点 1 的左子树,找到节点 2;
- 遍历节点 2 的左子树,找到节点 4;
- 由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树;
- 由于节点 4 无右子树,因此节点 2 的左子树遍历完成,访问节点 2;
- 遍历节点 2 的右子树,找到节点 5;
- 由于节点 5 无左子树,因此访问节点 5 ,又因为节点 5 没有右子树,因此节点 1 的左子树遍历完成,访问节点 1 ,并遍历节点 1 的右子树,找到节点 3;
- 遍历节点 3 的左子树,找到节点 6;
- 由于节点 6 无左子树,因此访问节点 6,又因为该节点无右子树,因此节点 3 的左子树遍历完成,开始访问节点 3 ,并遍历节点 3 的右子树,找到节点 7;
- 由于节点 7 无左子树,因此访问节点 7,又因为该节点无右子树,因此节点 1 的右子树遍历完成,即整棵树遍历完成;
因此,图 1 中二叉树采用中序遍历得到的序列为:
4 2 5 1 6 3 7
Recursion
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def inorder(root):
if not root:
return
inorder(root.left)
res.append(root.val)
inorder(root.right)
return
inorder(root)
return res
Iterative (Without recursion)
- use stack
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
cur = root # cur 指向当前要被扫描的节点
while cur or stack: # 只有当前指向的节点为 None 且之前放进 stack 的节点都被处理
while cur: # 一直向左下找节点,直到其左下无节点了
stack.append(cur) # 之后要处理当前的中间节点,所以需要把中间节点存入 stack
cur = cur.left
cur = stack.pop(-1) # 当前最左下元素为空后,从 stack 中找到中序节点,处理它。之后再处理其右子树
res.append(cur.val)
cur = cur.right
ref
Postorder Traversal(后序遍历)
二叉树后序遍历的实现思想是:从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素。
例子
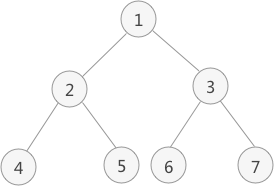
如上图中,对此二叉树进行后序遍历的操作过程为:
- 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点);
- 遍历节点 2 的左子树(以节点 4 为根节点);
- 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍历节点 2 的右子树(以 5 为根节点);
- 由于节点 5 无左右子树,因此可以访问节点 5 ,并且此时节点 2 的左右子树也遍历完成,因此也可以访问节点 2;
- 此时回退到节点 1 ,开始遍历节点 1 的右子树(以节点 3 为根节点);
- 遍历节点 3 的左子树(以节点 6 为根节点);
- 由于节点 6 无左右子树,因此访问节点 6,并回退到节点 3,开始遍历节点 3 的右子树(以节点 7 为根节点);
- 由于节点 7 无左右子树,因此访问节点 7,并且节点 3 的左右子树也遍历完成,可以访问节点 3;节点 1 的左右子树也遍历完成,可以访问节点 1;
- 到此,整棵树的遍历结束。
由此,对图 1 中二叉树进行后序遍历的结果为:
4 5 2 6 7 3 1
Recursive
public void postOrderTraverse1(TreeNode root) {
if (root != null) {
postOrderTraverse1(root.left);
postOrderTraverse1(root.right);
System.out.print(root.val+" ");
}
}
Iterative (Without recursion)
public void postOrderTraverse2(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode pNode = root;
while (true){
while(pNode != null){
stack.push(pNode);
if(pNode.right != null)
stack.push(pNode.right);
pNode = pNode.left;
}
if(stack.isEmpty())
return;
pNode = stack.pop();
if( pNode.right != null && ! stack.isEmpty() && current.right == stack.peek() ) {
stack.pop();
stack.push(pNode);
pNode = pNode.right;
} else {
System.out.print( pNode.data + " " );
pNode = null;
}
}
}
BFS (Breadth First Searchs,广度优先遍历)
具体的实现思路是:通过使用队列的数据结构,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。
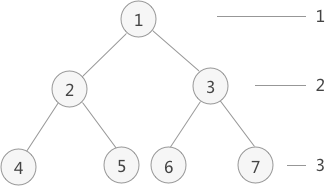
层次遍历上图中的二叉树:
- 首先,根结点 1 入队;
- 根结点 1 出队,出队的同时,将左孩子 2 和右孩子 3 分别入队;
- 队头结点 2 出队,出队的同时,将结点 2 的左孩子 4 和右孩子 5 依次入队;
- 队头结点 3 出队,出队的同时,将结点 3 的左孩子 6 和右孩子 7 依次入队;
- 不断地循环,直至队列内为空。
Preorder(前序遍历)
- use queue
def maxDepth(self, root):
"""
:type root: Optional[TreeNode]
:rtype: int
"""
if not root:
return 0
depth = 0
queue = [root]
while queue:
for _ in range(len(queue)): # traverse all nodes of the current level
node = queue.pop(0)
# add its children only if they are not None
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
depth += 1 # the node added to the queue is guaranteed not being None, and thus we could always +1 level
return depth
解析
NICE binary tree
Question description
A NICE binary tree has the following properties:
- root.val = 0
- If treeNode.val is x and treeNode.left != null, then treeNode.left.val = 2 * x + 1
- If treeNode.val is x and treeNode.right != null, then treeNode.right.val = 2 * x + 2
Now the NICE tree is reseted, which means all treeNode.val have been changed to -1.
Implement the TreeRecover class:
- TreeRecover(TreeNode* root) Initializes the object with a reseted binary tree and recovers it into a NICE binary tree.
- bool query(int target) Returns true if the target value exists in the NICE binary tree
- The key insight is that for a given node value x, its left child is 2 * x + 1 and its right child is 2 * x + 2. This property allows us to determine the path to follow (left or right) for a specific target value without needing to traverse the entire tree.
class TreeNode:
def __init__(self, v):
self.val = v
self.left = None
self.right = None
class Solution:
def check(self, root, target):
found = [False]
def dfs(root, target):
if not root:
return
if root.val == target:
found[0] = True
return
t = target
while True:
if t < root.val:
return
if (root.left and t == root.left.val) or (root.right and t == root.right.val):
if root.left and t == root.left.val:
dfs(root.left, target)
return
if root.right and t == root.right.val:
dfs(root.right, target)
return
reminder = t % 2
if reminder == 0:
t = t / 2 - 1
else:
t = (t - 1) / 2
dfs(root, target)
return found[0]
def construct(self):
root = TreeNode(0)
n1 = TreeNode(1)
n2 = TreeNode(2)
root.left = n1
root.right = n2
n3 = TreeNode(3)
n4 = TreeNode(4)
n1.left = n3
n2.right = n4
n5 = TreeNode(5)
n6 = TreeNode(6)
n2.left = n5
n2.right = n6
n7 = TreeNode(7)
n8 = TreeNode(8)
n3.left = n7
n3.right = n8
n9 = TreeNode(9)
n10 = TreeNode(10)
n4.left = n9
n4.right = n10
n11 = TreeNode(11)
n12 = TreeNode(12)
n5.left = n11
n5.right = n12
n13 = TreeNode(13)
n6.left = n13
return root
if __name__ == '__main__':
s = Solution()
root = s.construct()
print(s.check(root, 13))
Traversal
前序遍历 - DFS/BFS - 100. Same Tree
- 先看当前节点是否相同(是否不为None,且值相同)
- 再看当前节点的左子树 和 右子树 是否相同
# DPS - recursive
# - time: O(n)
# - space: O(h) # h is the height of the tree.
# - best case (balanced tree): O(logn)
# - worst case (degenerate tree): O(n)
def isSameTree(self, p, q):
"""
:type p: Optional[TreeNode]
:type q: Optional[TreeNode]
:rtype: bool
"""
if not p and not q:
return True
if p and q and p.val == q.val:
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
else:
return False
# DFS - Iterative (use Stack) via preorder
# - time: O(n)
# - space: O(n)
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
stack = [(p, q)]
while stack:
node1, node2 = stack.pop()
if not node1 and not node2:
continue
if not node1 or not node2 or node1.val != node2.val:
return False
stack.append((node1.right, node2.right))
stack.append((node1.left, node2.left))
return True
# BFS - Iterative (use Stack) via preorder
# - time: O(n)
# - space: O(n)
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
q1 = deque([p])
q2 = deque([q])
while q1 and q2:
for _ in range(len(q1)):
nodeP = q1.popleft()
nodeQ = q2.popleft()
if nodeP is None and nodeQ is None:
continue
if nodeP is None or nodeQ is None or nodeP.val != nodeQ.val:
return False
q1.append(nodeP.left)
q1.append(nodeP.right)
q2.append(nodeQ.left)
q2.append(nodeQ.right)
return True
ref
前序遍历 - 572. Subtree of Another Tree
# DFS
# - time: O(s*t)
# - space:O(s*t)
def isSubtree(self, root, subRoot):
"""
:type root: Optional[TreeNode]
:type subRoot: Optional[TreeNode]
:rtype: bool
"""
def sameTree(p, q): # define a helper function
if not p and not q:
return True
if p and q and p.val == q.val:
return (sameTree(p.left, q.left) and
sameTree(p.right, q.right))
else:
return False
if not subRoot: # None 是任何树的子树
return True
if not root: # None 中不存在任何子树 是 任何非空树的子树
return False
if sameTree(root, subRoot):
return True
return (self.isSubtree(root.left, subRoot) or
self.isSubtree(root.right,
subRoot))
# ??
# Serialization And Pattern Matching
# - time: O(s+t)
# - space: O(s+t)
def serialize(self, root: Optional[TreeNode]) -> str:
if root == None:
return "$#"
return ("$" + str(root.val) +
self.serialize(root.left) + self.serialize(root.right))
def z_function(self, s: str) -> list:
z = [0] * len(s)
l, r, n = 0, 0, len(s)
for i in range(1, n):
if i <= r:
z[i] = min(r - i + 1, z[i - l])
while i + z[i] < n and s[z[i]] == s[i + z[i]]:
z[i] += 1
if i + z[i] - 1 > r:
l, r = i, i + z[i] - 1
return z
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
serialized_root = self.serialize(root)
serialized_subRoot = self.serialize(subRoot)
combined = serialized_subRoot + "|" + serialized_root
z_values = self.z_function(combined)
sub_len = len(serialized_subRoot)
for i in range(sub_len + 1, len(combined)):
if z_values[i] == sub_len:
return True
return False
ref
前序遍历 - 112. Path Sum
# DFS - 写法 1
# - time: O(n)
# - space: O(n), O(n) for recursion stack
def hasPathSum(self, root, targetSum):
"""
:type root: Optional[TreeNode]
:type targetSum: int
:rtype: bool
"""
res = [False]
def dfs(root, leftSum):
if not root:
return
if res[0]:
return
if not root.left and not root.right and leftSum == root.val:
res[0] = True
return
leftSum = leftSum - root.val
dfs(root.left, leftSum)
dfs(root.right, leftSum)
dfs(root, targetSum)
return res[0]
# DFS - 写法 2
# - time: O(n)
# - space: O(n), O(n) for recursion stack
def hasPathSum(self, root, targetSum):
"""
:type root: Optional[TreeNode]
:type targetSum: int
:rtype: bool
"""
if not root:
return False
targetSum -= root.val
return ((not root.left and not root.right and targetSum == 0)
or self.hasPathSum(root.left, targetSum)
or self.hasPathSum(root.right, targetSum))
# BFS
# - time: O(n)
# - space: O(n), O(n) for queue
def hasPathSum(self, root, targetSum):
"""
:type root: Optional[TreeNode]
:type targetSum: int
:rtype: bool
"""
if not root:
return False
queue = [(root, targetSum)]
while queue:
n, leftSum = queue.pop(0)
leftSum -= n.val
if leftSum == 0 and not n.left and not n.right:
return True
if n.left:
queue.append((n.left, leftSum))
if n.right:
queue.append((n.right, leftSum))
return False
ref
前序遍历 - 114. Flatten Binary Tree to Linked List
# DFS - recursion
# - time: O(n)
# - space: O(n)
def flatten(self, root):
"""
:type root: Optional[TreeNode]
:rtype: None Do not return anything, modify root in-place instead.
"""
# dfs 返回当前树的 tail
# tail 的定义:中序遍历该树的最后一个节点
def dfs(root):
if not root:
return None
leftTail = dfs(root.left)
rightTail = dfs(root.right)
if root.left: # 如果有左子树
# 把左子树的 tail 的 right 连接到 root.right
leftTail.right = root.right
# 把当前节点连接到 左子树的根节点
root.right = root.left
# 把当前节点的 left 置为 None
root.left = None
if rightTail:
# 存在右子树,则返回 rightTail
return rightTail
if leftTail:
return leftTail
return root
dfs(root)
# DFS - iterative
# - time: O(n)
# - space: O(n)
def flatten(self, root):
"""
:type root: Optional[TreeNode]
:rtype: None Do not return anything, modify root in-place instead.
"""
if not root:
return None
stack = [root]
p = None
while stack:
n = stack.pop(-1)
if p:
p.right = n
p.left = None
p = n
if n.right:
stack.append(n.right)
if n.left:
stack.append(n.left)
return root
ref
BFS - 116. Populating Next Right Pointers in Each Node
# BFS
# - time: O(n)
# - space: O(n), O(n) for queue, as the lowest level has n/2 nodes
def connect(self, root):
"""
:type root: Node
:rtype: Node
"""
if not root:
return None
queue = [root]
while queue:
levelTotal = len(queue)
prev = None
for _ in range(levelTotal):
n = queue.pop(0)
if prev:
prev.next = n
prev = n
if n.left:
queue.append(n.left)
if n.right:
queue.append(n.right)
return root
# BFS - optimal
# - time: O(n)
# - space: O(1)
def connect(self, root):
"""
:type root: Node
:rtype: Node
"""
if not root:
return root
parent = root
while parent.left: # 如果有下一个level,则这个 loop 以处理每个level
nextLevelFirstNode = parent.left # 需要记下 下个level的开始节点
# 开始处理 parent 所处 level 的下面一个 level 的所有节点
while parent:
# 把右子节点赋值给左子节点的next
parent.left.next = parent.right
# 这一步很聪明
if parent.next:
parent.right.next = parent.next.left
parent = parent.next
parent = nextLevelFirstNode
return root
# DFS - optimal
# - time: O(n)
# - space: O(n), O(n) for recursion stack
def connect(self, root):
"""
:type root: Node
:rtype: Node
"""
if not root:
return root
if root.left:
root.left.next = root.right
if root.next:
root.right.next = root.next.left
self.connect(root.left)
self.connect(root.right)
return root
ref
- https://neetcode.io/solutions/populating-next-right-pointers-in-each-node
- https://www.youtube.com/watch?v=U4hFQCa1Cq0
前序遍历 - DFS/BFS - 226. Invert Binary Tree
- 前序遍历:先对换节点,再去处理子节点们(对子节点们进行递归处理)
# DFS - recursion
# - time: O(n)
# - space: O(1)
class Solution(object):
def invertTree(self, root):
"""
:type root: Optional[TreeNode]
:rtype: Optional[TreeNode]
"""
if not root:
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
# DFS - interative
# - use stack to achieve
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
stack = [root]
while stack:
node = stack.pop()
node.left, node.right = node.right, node.left
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return root
# BFS
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
queue = deque([root])
while queue:
node = queue.popleft()
node.left, node.right = node.right, node.left
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return root
ref
前序遍历 - DFS/BFS - 1448. Count Good Nodes in Binary Tree
- 前序遍历:先处理当前节点,再处理其左右子树
# DFS
# - 递归时,把 maxVal 传递下去,该值记录了,从 root 到当前节点经过的 path 上的所有节点的最大值。
# - 如果当前节点的值 >= 该值,该节点是一个 good node
# - root 永远是 good node
# - time: O(n)
# - space: O(n)
def goodNodes(self, root):
"""
:type root: TreeNode
:rtype: int
"""
res = [0]
def dfs(node, maxVal):
if not node:
return
# 递归时,把 maxVal 传递下去,该值记录了,从 root 到当前节点经过的 path 上的所有节点的最大值。
# 如果当前节点的值 >= 该值,该节点是一个 good node
if node.val >= maxVal:
res[0] += 1
maxVal = max(maxVal, node.val) # 更新当前看到过的最大值
dfs(node.left, maxVal)
dfs(node.right, maxVal)
dfs(root, root.val)
return res[0]
# BFS
# - time: O(n)
# - space: O(n)
def goodNodes(self, root: TreeNode) -> int:
res = [0]
def bfs(root):
if not root:
return
queue = [(root, -10000000)] # (node, max_val_in_path)
while queue:
for i in range(len(queue)):
n, max_val_in_path = queue.pop(0)
if n.val >= max_val_in_path:
res[0] += 1
if n.left:
queue.append((n.left, max(max_val_in_path, n.val)))
if n.right:
queue.append((n.right, max(max_val_in_path, n.val)))
bfs(root)
return res[0]
ref
- https://www.youtube.com/watch?v=7cp5imvDzl4
- https://neetcode.io/problems/count-good-nodes-in-binary-tree
BFS
前序遍历 - 102. Binary Tree Level Order Traversal
- 用
for i in range(len(queue))来记下当前这一层,一共有多少个不为空的节点,当遍历完他们后,就可以res.append(level),因为这一层已经遍历完了
# BFS
# - time: O(n)
# - space: O(n)
def levelOrder(self, root):
"""
:type root: Optional[TreeNode]
:rtype: List[List[int]]
"""
if not root:
return []
res = []
queue = [root]
while queue:
cur_level = []
levelToal = len(queue)
for _ in range(levelToal): # 当前queue中有多少个元素,则for loop多少次
node = queue.pop(0)
cur_level.append(node.val)
if node.left: # 保证 node 不为空时,才插入queue
queue.append(node.left)
if node.right: # 保证 node 不为空时,才插入queue
queue.append(node.right)
res.append(cur_level)
Ref
前序遍历 - 103. Binary Tree Zigzag Level Order Traversal
# BFS
# - 如果是奇数层,在插入 res 前,把 curLevel reverse
# time: O(n), # O(2n) -> O(n) to build each level, O(n) to reverse it
# space: O(n), max is O(n/2), as the queue occupies by the lowest level is n/2
def zigzagLevelOrder(self, root):
"""
:type root: Optional[TreeNode]
:rtype: List[List[int]]
"""
if not root:
return []
res = []
queue = [root]
while queue:
curLevel = []
levelTotal = len(queue)
for _ in range(levelTotal):
node = queue.pop(0)
curLevel.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
if len(res) % 2 == 1: # 如果是奇数层,在插入 res 前,把 curLevel reverse
curLevel = curLevel[::-1]
res.append(curLevel)
return res
# BFS - optimal(挺聪明的办法)
# - 如果是奇数层,在插入 res 前,直接把该元素插入到 curLevel 对应的正确位置
# time: O(n) -> O(n) to build each level
# space: O(n), max is O(n/2), as the queue occupies by the lowest level is n/2
def zigzagLevelOrder(self, root):
"""
:type root: Optional[TreeNode]
:rtype: List[List[int]]
"""
if not root:
return []
res = []
queue = [root]
while queue:
levelTotal = len(queue)
curLevel = [0] * levelTotal
for i in range(levelTotal):
if len(res) % 2 == 1:
i = levelTotal - i - 1
node = queue.pop(0)
curLevel[i] = node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(curLevel)
return res
ref
- https://www.youtube.com/watch?v=igbboQbiwqw
- https://neetcode.io/solutions/binary-tree-zigzag-level-order-traversal
前序遍历 - 199. Binary Tree Right Side View
# BFS(更 comes in nature)
# - time: O(n)
# - space: O(n)
def rightSideView(self, root):
"""
:type root: Optional[TreeNode]
:rtype: List[int]
"""
if not root:
return []
res = []
queue = [root]
while queue:
levelTotal = len(queue) # 记录下当时 queue 里有的元素的个数(当前 level 有的元素的个数)
for i in range(levelTotal):
n = queue.pop(0)
if i == levelTotal - 1: # 如果当前元素为当前 level 元素的最后一个
res.append(n.val)
if n.left:
queue.append(n.left)
if n.right:
queue.append(n.right)
return res
# DFS
# - time: O(n)
# - space: O(n)
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
res = []
def dfs(node, depth):
if not node:
return None
if depth == len(res):
res.append(node.val)
dfs(node.right, depth + 1)
dfs(node.left, depth + 1)
dfs(root, 0)
return res
ref
- https://www.youtube.com/watch?v=d4zLyf32e3I
- https://neetcode.io/problems/binary-tree-right-side-view
Depth
前序遍历 - DFS/BFS - 104. Maximum Depth of Binary Tree
-
前序遍历
-
类似的问题:如果把根节点看做第 1 层,如何打印出每一个节点所在的层数?
-
def printCurDepth(self, root: Optional[TreeNode]) -> int: def dfs(root, parent_depth): if not root: return 0 cur_depth = parent_depth + 1 print(cur_depth) dfs(root.left, cur_depth) dfs(root.right, cur_depth) dfs(root, 0)
-
# DPS - recursive
# - time: O(n)
# - space: O(h) # h is the height of the tree.
# - best case (balanced tree): O(logn)
# - worst case (degenerate tree): O(n)
class Solution(object):
def maxDepth(self, root):
"""
:type root: Optional[TreeNode]
:rtype: int
"""
if not root: # 如果该节点为空,则该子树的depth为0
return 0
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right)) # 因为此时 root不为 None,因而其本身使得 height + 1
# DFS - Iterative (use Stack) via preorder
# - time: O(n)
# - space: O(n)
class Solution:
def maxDepth(self, root):
"""
:type root: Optional[TreeNode]
:rtype: int
"""
if not root:
return 0
max_depth = 1
stack = [(root, 1)] # (node, depth)
while stack:
node, depth = stack.pop(0)
max_depth = max(max_depth, depth)
if node.left:
stack.append((node.left, depth + 1))
if node.right:
stack.append((node.right, depth + 1))
return max_depth
# BFS (use queue)
# - time: O(n)
# - space: O(n)
class Solution:
def maxDepth(self, root):
"""
:type root: Optional[TreeNode]
:rtype: int
"""
if not root:
return 0
depth = 0
queue = [root]
while queue:
for _ in range(len(queue)): # traverse all nodes of the current level
node = queue.pop(0)
# add its children only if they are not None
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
depth += 1 # the node added to the queue is guaranteed not being None, and thus we could always +1 level
return depth
ref
后序遍历 - DFS - 110. Balanced Binary Tree
- 判断是否balanced:
abs(left_height - right_height) <= 1
# DPS - recursive
# - time: O(n)
# - space: O(h) # Count the space used by the call-stack. If not, it is O(1). h is the height of the tree.
# - best case (balanced tree): O(logn)
# - worst case (degenerate tree): O(n)
def isBalanced(self, root):
"""
:type root: Optional[TreeNode]
:rtype: bool
"""
res = [True]
def dfs(node):
if not res[0]: # If found not-balance, no need to cal further
return 0
if not node:
return 0
left_height = dfs(node.left)
right_height = dfs(node.right)
# compare the diff between left_height and right_height to know the balance
if abs(left_height - right_height) > 1:
res[0] = False
return max(left_height, right_height) + 1 # 因为此时 node 不为空,找到一个节点时,height就可以加1
dfs(root)
return res[0]
# DFS - Iterative (use Stack) via preorder
# - time: O(n)
# - space: O(n)
def isBalanced(self, root):
stack = []
node = root
last = None
depths = {}
while stack or node:
if node:
stack.append(node)
node = node.left
else:
node = stack[-1]
if not node.right or last == node.right:
stack.pop()
left = depths.get(node.left, 0)
right = depths.get(node.right, 0)
if abs(left - right) > 1:
return False
depths[node] = 1 + max(left, right)
last = node
node = None
else:
node = node.right
return True
ref
后序遍历 - DFS - 543. Diameter of Binary Tree
-
更像一个 medium 问题
-
后序遍历
-
思路
-
Diameter = 左子树的 depth + 右子树的 depth
-
用一个全部变量记下当前看过的最大的 diameter
-
dfs函数返回以当前节点作为根节点的数的最大depth -
如果一个节点没有左子树,则左侧的depth为0
-
-
类似的问题:打印出每个节点的左右子树各有多少节点?
-
# DFS def printSubTreeNodeNum(self, root: Optional[TreeNode]) -> int: if not root: return 0 left_num = self.printSubTreeNum(root.left) right_num = self.printSubTreeNum(root.right) print("left_sub_tree_node_num:", left_num) print("right_sub_tree_node_num:", right_num) return left_num + right_num + 1
-
# DFS - recursion
# - space: O(h) # h is the height of the tree.
# - best case (balanced tree): O(logn)
# - worst case (degenerate tree): O(n)
def diameterOfBinaryTree(self, root):
"""
:type root: Optional[TreeNode]
:rtype: int
"""
res = [0] # 用 [0] 而不是 0 来避免报错
def dfs(node):
if not node:
return 0
left_height = dfs(node.left)
right_height = dfs(node.right)
# 计算出当前节点的 diameter,更新到 res 中
cur_diameter = left_height + right_height
res[0] = max(cur_diameter, res[0])
return max(left_height, right_height) + 1 # 返回当前节点的最高高度(考虑了左子树和右子树)
dfs(root)
return res[0]
# DFS - Iterative
# - time: O(n)
# - space: O(n)
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
stack = [root]
mp = {None: (0, 0)}
while stack:
node = stack[-1]
if node.left and node.left not in mp:
stack.append(node.left)
elif node.right and node.right not in mp:
stack.append(node.right)
else:
node = stack.pop()
leftHeight, leftDiameter = mp[node.left]
rightHeight, rightDiameter = mp[node.right]
mp[node] = (1 + max(leftHeight, rightHeight),
max(leftHeight + rightHeight, leftDiameter, rightDiameter))
return mp[root][1]
Ref
Construct Binary Tree by Traversal
105. Construct Binary Tree from Preorder and Inorder Traversal
- 如果 len(preorder) == 0,直接不需要构造Tree
- 如果 len(preorder) > 0,root 节点一定是preorder[0],因为先序遍历的规律就是先访问 root 节点
- 然后在中序遍历的结果中,找到这个 root 节点的索引位置,在中序遍历中,该 root 节点左边的那些节点,就是该 root 节点的左子树的节点,因为中序遍历的规律就是访问完左子树后,才访问 root 节点
- 又因为中序遍历的规律就是访问完 root 节点后,才访问右子树,所以root 节点后的那些节点,就是该 root 节点的右子树的节点
- 因为无论是前序遍历还是中序遍历,都是最后访问右子树,所以对于中序遍历和前序遍历,访问完 root 节点后要访问的节点都是属于右子树的节点
- 递归
preorder: [3 9 20 15 7]
inorder: [9 3 15 20 7]
-> 说明 root 节点是 3
-> 去 inorder 中,找到 root 节点的索引,即 1
-> 所以 inorder[0:(1)] 是左子树的 inorder
-> 左子树的 preorder 是 preorder[(1): (1) + 1]
-> 右子树的 inorder 是 inorder[(1) + 1:]
-> 右子树的 preorder 是 preorder[(1) + 1:]
# DFS
# - time: O(n^2) # 递归 O(n) + find_by_index O(n)
# - space: O(n)
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if len(preorder) == 0:
return None
v = preorder[0]
parent = TreeNode(v)
inorder_spliter_idx = inorder.index(v)
left_preorder = preorder[1:inorder_spliter_idx + 1]
left_inorder = inorder[:inorder_spliter_idx]
parent.left = self.buildTree(left_preorder, left_inorder)
right_preorder = preorder[inorder_spliter_idx + 1:]
right_inorder = inorder[inorder_spliter_idx + 1:]
parent.right = self.buildTree(right_preorder, right_inorder)
return parent
# DFS + hashmap
# - time: O(n) # 递归 O(n) + find_by_index O(1)
# - space: O(n) # 除去返回的答案需要的 O(n) 空间之外,我们还需要使用 O(n) 的空间存储哈希映射,以及 O(h)(其中 h 是树的高度)的空间表示递归时栈空间。这里 h<n,所以总空间复杂度为 O(n)。
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
indices = {val: idx for idx, val in enumerate(inorder)}
self.pre_idx = 0
def dfs(l, r):
if l > r:
return None
root_val = preorder[self.pre_idx]
self.pre_idx += 1
root = TreeNode(root_val)
mid = indices[root_val]
root.left = dfs(l, mid - 1)
root.right = dfs(mid + 1, r)
return root
return dfs(0, len(inorder) - 1)
# DFS (optimal)
# - time: O(n) # 递归 O(n)
# - space: O(n) # for recursion stack
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
preIdx = inIdx = 0
def dfs(limit):
nonlocal preIdx, inIdx
if preIdx >= len(preorder):
return None
if inorder[inIdx] == limit:
inIdx += 1
return None
root = TreeNode(preorder[preIdx])
preIdx += 1
root.left = dfs(root.val)
root.right = dfs(limit)
return root
return dfs(float('inf'))
ref
- https://www.youtube.com/watch?v=ihj4IQGZ2zc
- https://neetcode.io/problems/binary-tree-from-preorder-and-inorder-traversal
- https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solutions/255811/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/
106. Construct Binary Tree from Inorder and Postorder Traversal
# DFS
# - time: O(n^2) # 递归 O(n) + find_by_index O(n)
# - space: O(n)
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
if not postorder or not inorder:
return None
root = TreeNode(postorder[-1])
mid = inorder.index(postorder[-1])
root.left = self.buildTree(inorder[:mid], postorder[:mid])
root.right = self.buildTree(inorder[mid + 1:], postorder[mid:-1])
return root
# DFS + hashmap
# - time: O(n) # 递归 O(n) + find_by_index O(1)
# - space: O(n) # 除去返回的答案需要的 O(n) 空间之外,我们还需要使用 O(n) 的空间存储哈希映射,以及 O(h)(其中 h 是树的高度)的空间表示递归时栈空间。这里 h<n,所以总空间复杂度为 O(n)。
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
inorderIdx = {v: i for i, v in enumerate(inorder)}
def dfs(l, r):
if l > r:
return None
root = TreeNode(postorder.pop())
idx = inorderIdx[root.val]
root.right = dfs(idx + 1, r)
root.left = dfs(l, idx - 1)
return root
return dfs(0, len(inorder) - 1)
# DFS (optimal)
# - time: O(n) # 递归 O(n)
# - space: O(n) # for recursion stack
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
postIdx = inIdx = len(postorder) - 1
def dfs(limit):
nonlocal postIdx, inIdx
if postIdx < 0:
return None
if inorder[inIdx] == limit:
inIdx -= 1
return None
root = TreeNode(postorder[postIdx])
postIdx -= 1
root.right = dfs(root.val)
root.left = dfs(limit)
return root
return dfs(float('inf'))
ref
- https://neetcode.io/solutions/construct-binary-tree-from-inorder-and-postorder-traversal
- https://www.youtube.com/watch?v=vm63HuIU7kw
889. Construct Binary Tree from Preorder and Postorder Traversal
def constructFromPrePost(self, preorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
if not preorder:
return None
root_val = preorder[0]
root = TreeNode(root_val)
preorder_splitter_idx = 0
preorder_set = set()
postorder_set = set()
for idx in range(1, len(preorder)):
preorder_set.add(preorder[idx])
postorder_set.add(postorder[idx - 1])
if preorder_set == postorder_set:
preorder_splitter_idx = idx
break
root.left = self.constructFromPrePost(preorder[1:preorder_splitter_idx + 1], postorder[0:preorder_splitter_idx])
root.right = self.constructFromPrePost(preorder[preorder_splitter_idx + 1:],
postorder[preorder_splitter_idx:len(postorder) - 1])
return root
序列化
比如说,如果给你一棵二叉树的前序遍历结果,你是否能够根据这个结果还原出这棵二叉树呢?
答案是也许可以,也许不可以,具体要看你给的前序遍历结果是否包含空指针的信息。如果包含了空指针,那么就可以唯一确定一棵二叉树,否则就不行。
举例来说,如果我给你这样一个不包含空指针的前序遍历结果 [1,2,3,4,5],那么如下两棵二叉树都是满足这个前序遍历结果的:

所以给定不包含空指针信息的前序遍历结果,是不能还原出唯一的一棵二叉树的。
但如果我的前序遍历结果包含空指针的信息,那么就能还原出唯一的一棵二叉树了。比如说用 # 表示空指针,上图左侧的二叉树的前序遍历结果就是 [1,2,3,#,#,4,#,#,5,#,#],上图右侧的二叉树的前序遍历结果就是 [1,2,#,3,#,#,4,5,#,#,#],它俩就区分开了。
那么估计就有聪明的小伙伴说了:东哥我懂了,甭管是前中后序哪一种遍历顺序,只要序列化的结果中包含了空指针的信息,就能还原出唯一的一棵二叉树了。
首先要夸一下这种举一反三的思维,但很不幸,正确答案是,即便你包含了空指针的信息,也只有前序和后序的遍历结果才能唯一还原二叉树,中序遍历结果做不到。
本文后面会具体探讨这个问题,这里只简单说下原因:因为前序/后序遍历的结果中,可以确定根节点的位置,而中序遍历的结果中,根节点的位置是无法确定的。
更直观的,比如如下两棵二叉树显然拥有不同的结构,但它俩的中序遍历结果都是 [#,1,#,1,#],无法区分:

说了这么多,总结下结论,当二叉树中节点的值不存在重复时:
-
如果你的序列化结果中不包含空指针的信息,且你只给出一种遍历顺序,那么你无法还原出唯一的一棵二叉树。
-
如果你的序列化结果中不包含空指针的信息,且你会给出两种遍历顺序,那么按照前文 东哥手把手带你刷二叉树(构造篇) 所说,分两种情况:
- 如果你给出的是前序和中序,或者后序和中序,那么你可以还原出唯一的一棵二叉树。
- 如果你给出前序和后序,那么你无法还原出唯一的一棵二叉树。
-
如果你的序列化结果中包含空指针的信息,且你只给出一种遍历顺序,也要分两种情况:
- 如果你给出的是前序或者后序,那么你可以还原出唯一的一棵二叉树。
- 如果你给出的是中序,那么你无法还原出唯一的一棵二叉树。
Ref
todo - 297. Serialize and Deserialize Binary Tree
class Codec:
def serialize(self, root):
res = []
def dfs(node):
if not node:
res.append("N")
return
res.append(str(node.val))
dfs(node.left)
dfs(node.right)
dfs(root)
return ",".join(res)
def deserialize(self, data):
vals = data.split(",")
self.i = 0
def dfs():
if vals[self.i] == "N":
self.i += 1
return None
node = TreeNode(int(vals[self.i]))
self.i += 1
node.left = dfs()
node.right = dfs()
return node
return dfs()
ref
- https://www.youtube.com/watch?v=u4JAi2JJhI8
- https://neetcode.io/solutions/serialize-and-deserialize-binary-tree
- https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-66994/dong-ge-da-d14d3/
652. Find Duplicate Subtrees
- 用 DFS 来序列化一个tree,成一个 string,比如 “1, 2, 3, 4, null, 2, 4, null, null, 4, null, null, null”,且配合一个hashmap 来判断是否其是否存在duplicate
- 如果存在,添加该 tree 的 root 到 res 中
# DFS + Serialization
# - time: O(n^2),对于每个节点,生成其 sign 需要 O(n), 而共有 n 个节点
# - space: O(n^2)
def findDuplicateSubtrees(self, root):
"""
:type root: Optional[TreeNode]
:rtype: List[Optional[TreeNode]]
"""
res = []
m = {}
def dfs(root):
if not root:
return "null"
sign = ",".join([str(root.val), dfs(root.left), dfs(root.right)])
if sign in m:
if len(m[sign]) == 1: # 之前没把这个节点添加到 res 过
res.append(root) # only need to return the root node
m[sign].append(root)
else:
m[sign] = [root]
return sign
dfs(root)
return res
ref
Misc
116. Populating Next Right Pointers in Each Node
# BFS with stack
# time: O(n)
# address: O(n)
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:
return None
queue = [root]
while queue:
t = None
for i in range(len(queue)):
node = queue.pop(0)
if node.left and node.right:
queue.append(node.left)
queue.append(node.right)
if t:
t.next = node
t = node
return root
# BFS without stack
# time: O(n)
# address: O(1)
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:
return None
cur = root
left = root.left
while cur and left: # go bottom
next_level_cur = cur.left
while cur: # go right
left.next = cur.right
if cur.next:
cur.right.next = cur.next.left
cur = cur.next
if cur:
left = cur.left
cur = next_level_cur
left = next_level_cur.left
return root
ref
- https://www.youtube.com/watch?v=U4hFQCa1Cq0
- https://neetcode.io/solutions/populating-next-right-pointers-in-each-node
236. Lowest Common Ancestor of a Binary Tree
# DFS
# - time: O(n), n 为节点数量
# - space: O(n), recursion stack used O(n) 在最坏情况下
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
if not root: # 当访问到了叶子结点,return None
return None
if root.val == p.val or root.val == q.val:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if not left:
# 当 left 为空,说明 p,q 都不在 root 的左子树中,直接返回 right
return right
if not right:
return left
# 当 left 和 right 同时不为空 :说明 p,q 分列在 root 的 异侧 (分别在 左 / 右子树),因此 root 为最近公共祖先,返回 root ;
return root # 当前节点为 LCA
ref
450. Delete Node in a BST
# time: O(h)
# space: O(h), O(h) for recursion stack
class Solution(object):
def findMin(self, root):
while root.left:
root = root.left
return root
def deleteNode(self, root, key):
"""
:type root: Optional[TreeNode]
:type key: int
:rtype: Optional[TreeNode]
"""
if not root:
return None
if key < root.val: # 去左子树找
root.left = self.deleteNode(root.left, key)
return root # 去右子树找
elif key > root.val:
root.right = self.deleteNode(root.right, key)
return root
else: # 当前节点是需要删除的节点
if not root.left and not root.right: # 左右子树都没有
return None
if not root.left: # 没有左子节点
return root.right
if not root.right: # 没有右子节点
return root.left
# 左右子节点都有
# 可以从右子树找最小值,也可以从右子树找最大值
minNode = self.findMin(root.right)
root.val = minNode.val # 把右子树中的最小值赋值给当前节点,然后在右子树里删除这个节点
root.right = self.deleteNode(root.right, minNode.val)
return root
ref
654. Maximum Binary Tree
# DFS - recursion
# - time: O(n^2),每个节点找 max 需要 O(n),需要处理 n 个节点
# - space: O(n)
def constructMaximumBinaryTree(self, nums):
"""
:type nums: List[int]
:rtype: Optional[TreeNode]
"""
if len(nums) == 0:
return None
maxValIdx = 0
for i in range(1, len(nums)):
if nums[i] > nums[maxValIdx]:
maxValIdx = i
node = TreeNode(nums[maxValIdx])
node.left = self.constructMaximumBinaryTree(nums[0:maxValIdx])
node.right = self.constructMaximumBinaryTree(nums[maxValIdx + 1:])
return node
# monotinic stack
# todo
# - time: O(n),
# - space: O(n)
ref