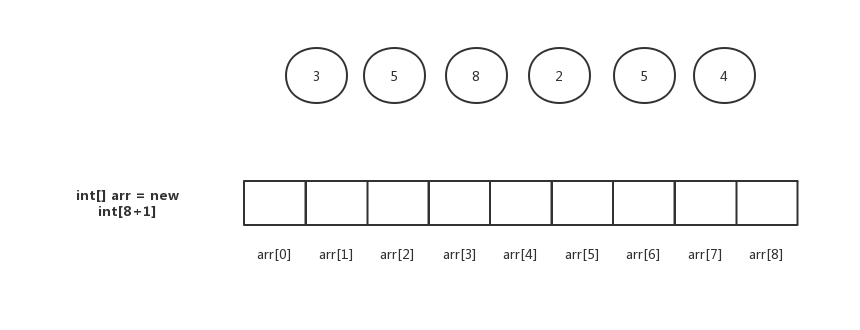
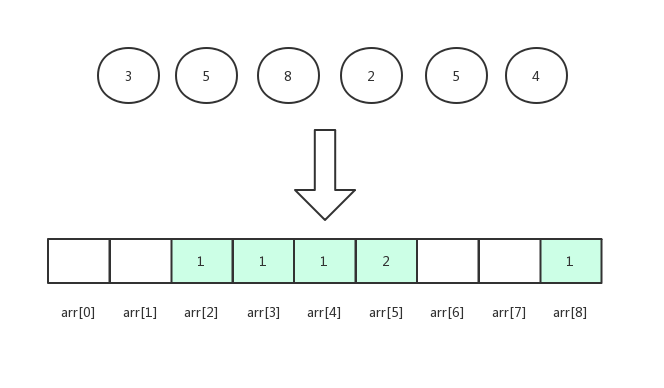
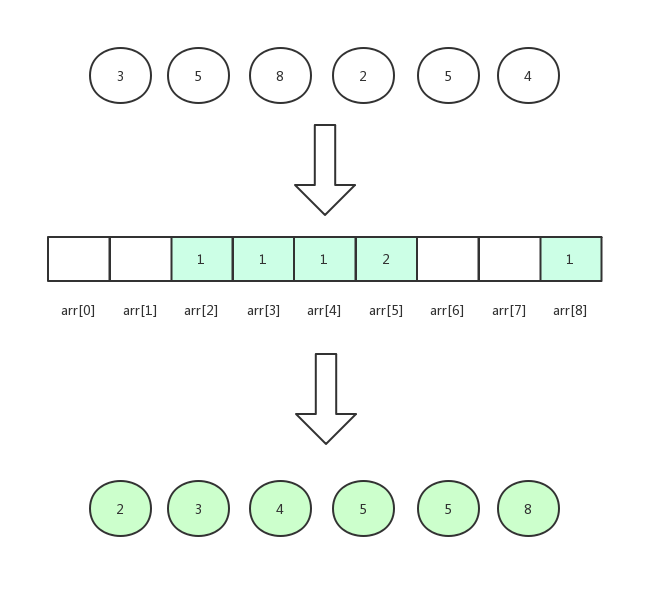
贪心算法(Greedy Algorithm)
贪心算法(Greedy Algorithm),又称贪婪算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。比如在旅行推销员问题中,如果旅行员每次都选择最近的城市,那这就是一种贪心算法。
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。简单地说,问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
我们能够依据贪心法的2个重要的性质去证明:贪心选择性质和最优子结构性质。
贪心选择
什么叫贪心选择?从字义上就是贪心也就是目光短线。贪图眼前利益。在算法中就是仅仅依据当前已有的信息就做出选择,并且以后都不会改变这次选择**(这是和动态规划法的主要差别)**。
所以对于一个具体的问题。要确定它是否具有贪心选择性质,必须证明每做一步贪心选择是否终于导致问题的总体最优解。
最优子结构
当一个问题的最优解包括其子问题的最优解时,称此问题具有最优子结构性质。
运用贪心策略在每一次转化时都取得了最优解。问题的最优子结构性质是该问题可用贪心算法或动态规划算法求解的关键特征。贪心算法的每一次操作都对结果产生直接影响,而动态规划则不是。贪心算法对每个子问题的解决方案都做出选择,不能回退;动态规划则会根据以前的选择结果对当前进行选择,有回退功能。动态规划主要运用于二维或三维问题,而贪心一般是一维问题。
基本思路
贪心算法的基本思路是从问题的某一个初始解触发一步一步地进行,根据抹个优化测度,每一步都要确保能获得局部最优解,每一步值考虑一个数据,他的选取应该满足局部优化的条件。若下一个数据和部分最优解连载一起不再是可行解时,就不把改数据添加到部分解中,知道把所有数据枚举玩,或者不能在添加算法停止。
过程
- 建立数学模型来描述问题;
- 把求解的问题分成若干个子问题;
- 对每一子问题求解,得到子问题的局部最优解;
- 把子问题的解局部最优解合成原来解问题的一个解。
...