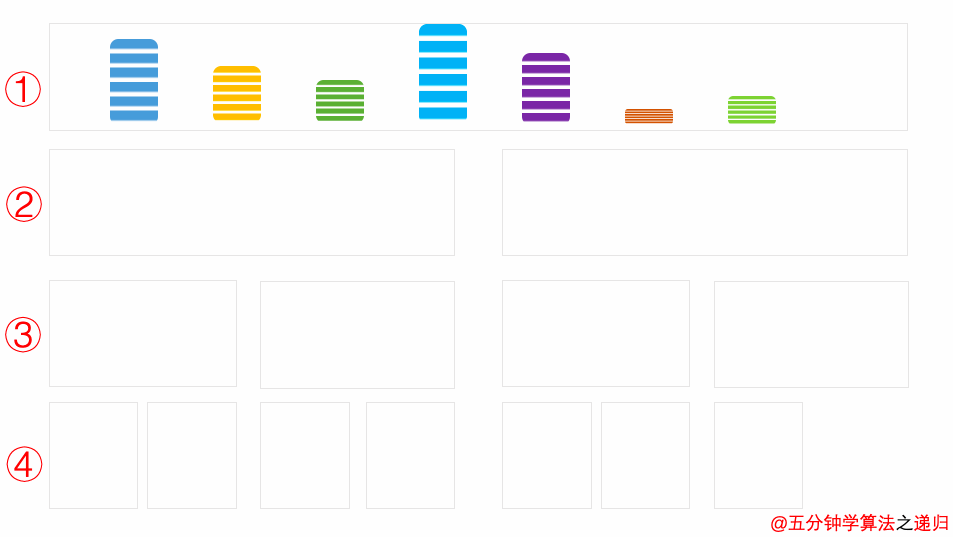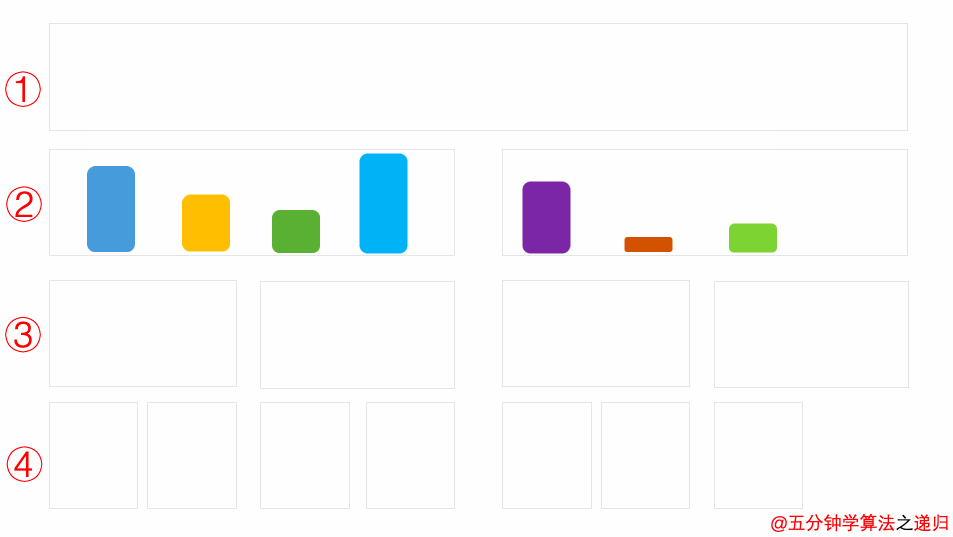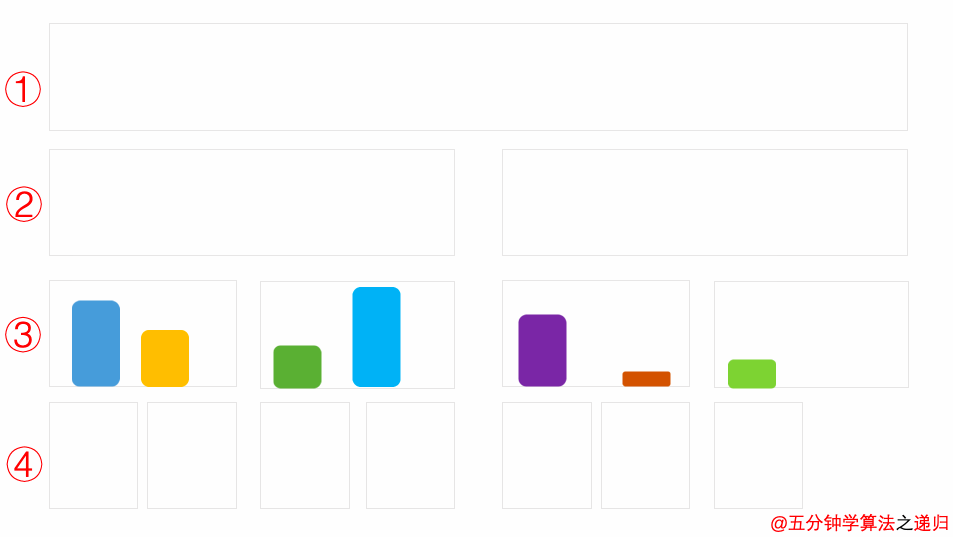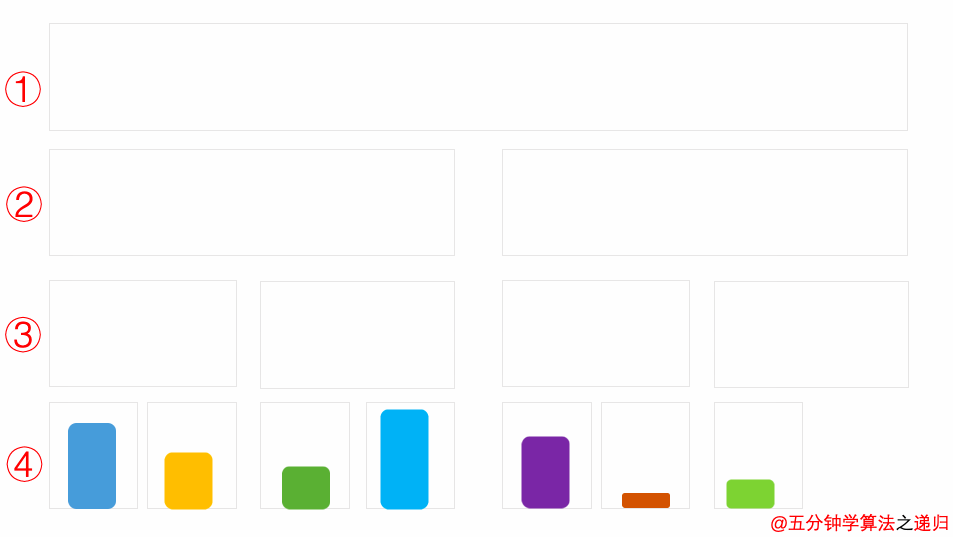
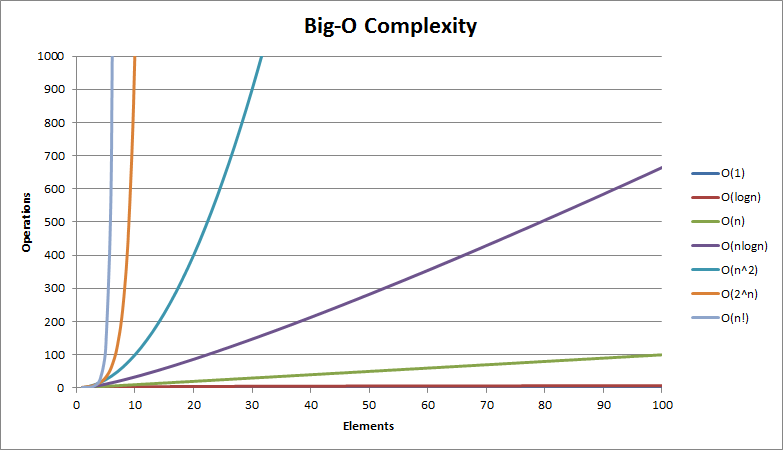
【Data Structure】优先队列（Priority Queue）- 堆（Heap）- 二叉堆（binary heap）

Background

这里来说明一下满二叉树（full binary tree）的概念与完全二叉树（complete binary tree）的概念。

满二叉树（Full Binary Tree）

A full binary tree is a binary tree in which all of the nodes have either 0 or 2 offspring. In other terms, a full binary tree is a binary tree in which all nodes, except the leaf nodes, have two offspring.

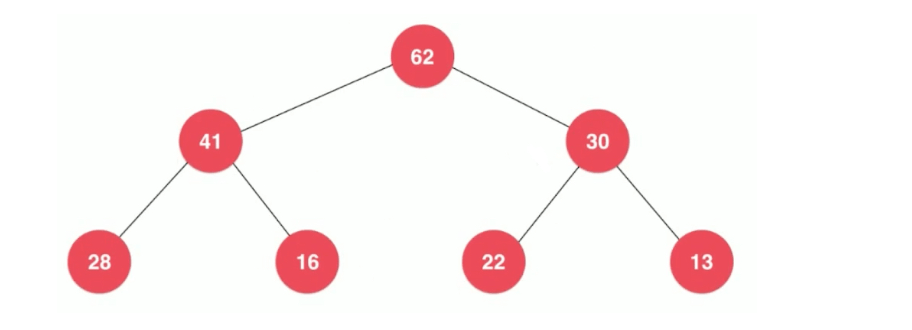
可以看出：满二叉树所有的节点都拥有左孩子，又拥有右孩子。

...

Posted by Wei on 2019-07-29, Last Modified on 2025-03-25

【Algorithm】算法思想 - 动态规划（Dynamic Programming）

Background

介绍动态规划之前先介绍一下分治策略（Divide and Conquer）。

分治策略

将原问题分解为若干个规模较小但类似于原问题的子问题（Divide），「递归」的求解这些子问题（Conquer），然后再合并这些子问题的解来建立原问题的解。

因为在求解大问题时，需要递归的求小问题，因此一般用「递归」的方法实现，即自顶向下。

动态规划（Dynamic Programming）

动态规划其实和分治策略是类似的，也是将一个原问题分解为若干个规模较小的子问题，递归的求解这些子问题，然后合并子问题的解得到原问题的解。区别在于这些子问题会有重叠，一个子问题在求解后，可能会再次求解，于是我们想到将这些子问题的解存储起来，当下次再次求解这个子问题时，直接拿过来就是。其实就是说，动态规划所解决的问题是分治策略所解决问题的一个子集，只是这个子集更适合用动态规划来解决从而得到更小的运行时间。

...

Posted by Wei on 2019-07-29, Last Modified on 2023-09-05

【Algorithm】递归（Recursion）

递归（Recursion）

先下定义：递归算法是一种直接或者间接调用自身函数或者方法的算法。

通俗来说，递归算法的实质是把问题分解成规模缩小的同类问题的子问题，然后递归调用方法来表示问题的解。它有如下特点：

一个问题的解可以分解为几个子问题的解
这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
存在递归终止条件，即必须有一个明确的递归结束条件，称之为递归出口

...

Posted by Wei on 2019-07-29, Last Modified on 2025-04-04

【Algorithm】BigNum 原理

背景

一些基本数据类型的范围：

int：32位整数，占4字节，-2^31~2^31-1(-21亿多~21亿多)
unsigned int：占4字节，0~2^32-1(0~42亿多) –10位数

VC的64位整数：

_int64：占8字节，-2^63~2^63-1（-900亿亿多~900亿亿多）
unsigned int64:占8字节，0~2^64-1(0~1800亿亿多)-20位数
G++的64位整数：
- long long==int64
- unsigned long long==unsigned __int64

实数：

float：占4字节，7位有效数字
double：占8字节，15位有效数字

浮点型的问题都是追求精度的，在一般情况下我们应当选择使用double，而很少用float；

所以当我们要进行计算的数超过了20位，我们就要用数组来模拟我们的计算过程了；

...

Posted by Wei on 2019-07-29, Last Modified on 2023-09-02

【Algorithm】算法的时间复杂度（Time Complexity）

常见的时间复杂度量级

我们先从常见的时间复杂度量级进行大O的理解：

常数阶O(1)
对数阶$O(log_2n)$
线性阶O(n)
线性对数阶$On(log_2n)$
平方阶$O(n^2)$
指数阶$O(2^n)$

复杂度	标记符号	描述
常量（Constant）	$O(1) $	操作的数量为常数，与输入的数据的规模无关。n = 1,000,000 -> 1-2 operations
对数（Logarithmic）	$O(log_2n)$	操作的数量与输入数据的规模 n 的比例是 log2 (n)。n = 1,000,000 -> 30 operations
线性（Linear）	$O(n)$	操作的数量与输入数据的规模 n 成正比。n = 10,000 -> 5000 operations
平方（Quadratic）	$O(n^2)$	操作的数量与输入数据的规模 n 的比例为二次平方。n = 500 -> 250,000 operations
立方（Cubic）	$O(n^3)$	操作的数量与输入数据的规模 n 的比例为三次方。n = 200 -> 8,000,000 operations
指数（Exponential）	$O(2^n)$、$O(k^n)$、$O(n!)$	指数级的操作，快速的增长。n = 20 -> 1048576 operations

列举了几种常见的算法时间复杂度的比较（又小到大）：$O(1)$（常数阶） < $O(log_2n)$（对数阶） < $O(n)$（线性阶） < $O(n2)$（平方阶） < $O(n3)$（立方阶） < $O(2^n)$ (指数阶)。

通常将以 10 为底的对数叫做常用对数。为了简便，N 的常用对数 log10 N 简写做 lg N，例如 log10 5 记做 lg 5。

通常将以无理数 e 为底的对数叫做自然对数。为了方便，N 的自然对数 loge N 简写做 ln N，例如 loge 3 记做 ln 3。

在算法导论中，采用记号 $lg n = log_2n$ ，也就是以 2 为底的对数。改变一个对数的底只是把对数的值改变了一个常数倍，所以当不在意这些常数因子时，我们将经常采用 “lg n"记号，就像使用 O 记号一样。计算机工作者常常认为对数的底取 2 最自然，因为很多算法和数据结构都涉及到对问题进行二分。

而通常时间复杂度与运行时间有一些常见的比例关系：

复杂度	10	20	50	100	1000	10000	100000
$O(1)$	<1s	<1s	<1s	<1s	<1s	<1s	<1s
$O(log_2(n))$	<1s	<1s	<1s	<1s	<1s	<1s	<1s
$O(n)$	<1s	<1s	<1s	<1s	<1s	<1s	<1s
$O(n*log_2(n))$	<1s	<1s	<1s	<1s	<1s	<1s	<1s
$O(n^2)$	<1s	<1s	<1s	<1s	<1s	2s	3-4 min
$O(n^3)$	<1s	<1s	<1s	<1s	20s	5 hours	231 days
$O(2^n)$	<1s	<1s	260 days	hangs	hangs	hangs	hangs
$O(n!)$	<1s	hangs	hangs	hangs	hangs	hangs	hangs
$O(n^n)$	3-4 min	hangs	hangs	hangs	hangs	hangs	hangs

...

Posted by Wei on 2019-07-27, Last Modified on 2023-09-02

西维蜀黍

【Data Structure】优先队列（Priority Queue）- 堆（Heap）- 二叉堆（binary heap）

Background

满二叉树（Full Binary Tree）

【Algorithm】算法思想 - 动态规划（Dynamic Programming）

Background

分治策略

动态规划（Dynamic Programming）

【Algorithm】递归（Recursion）

递归（Recursion）

【Algorithm】BigNum 原理

背景

【Algorithm】算法的时间复杂度（Time Complexity）

常见的时间复杂度量级

FEATURED TAGS

ABOUT ME

FRIENDS