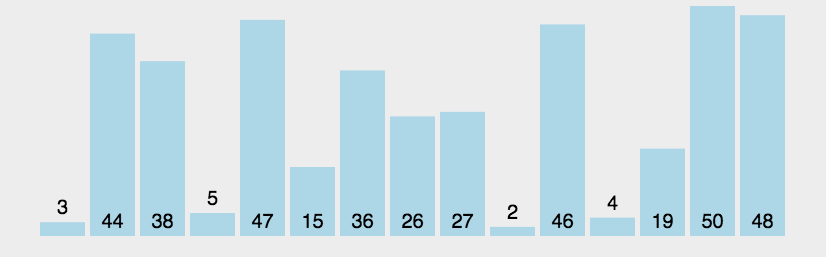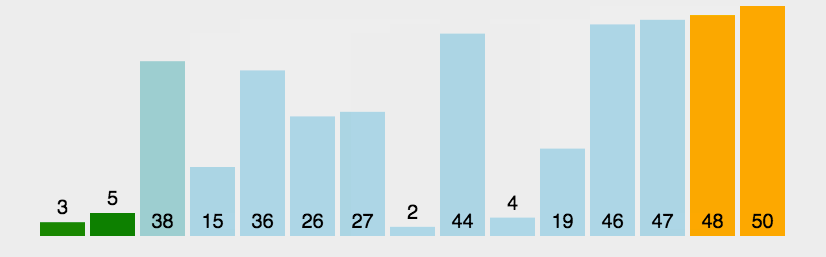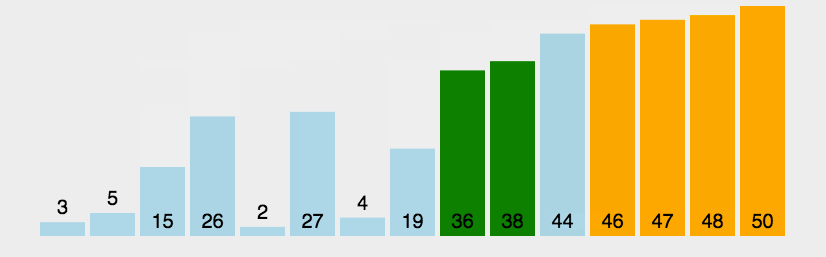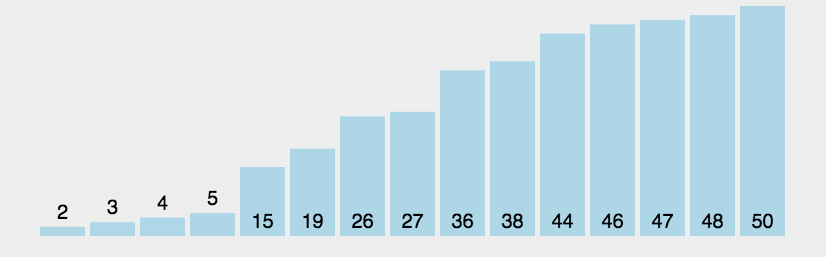【Algorithm】排序（Sorting）算法

排序算法的比较

算法	平均时间复杂度	最好时间复杂度	最坏时间复杂度	空间复杂度	排序方式	稳定性	备注
冒泡排序	$O (N^{2})$	$O (N)$	$O (N^{2})$	$O (1)$	In-place	稳定
选择排序	$O (N^{2})$	$O (N^{2})$	$O (N^{2})$	$O (1)$	In-place	稳定
插入排序	$O (N^{2})$	$O (N)$	$O (N^{2})$	$O (1)$	In-place	稳定	时间复杂度和初始顺序有关
希尔排序（Shell Sort）	$O (N l o g_{2} N)$	$O (N l o g_{2} N)$	$$O(N^2)$	$O (1)$	In-place	不稳定	改进版插入排序
归并排序（Merge Sort）	$O (N l o g_{2} N)$	$O (N l o g_{2} N)$	$O (N l o g_{2} N)$	$O (N)$	Out-place	不稳定
快速排序	$O (N l o g_{2} N)$	$O (N l o g_{2} N)$	$O (N^{2})$	$O (1)$	In-place	不稳定
堆排序（Heap Sort）	$O (N l o g_{2} N)$	$O (N l o g_{2} N)$	$O (N l o g_{2} N)$	$O (1)$	In-place	不稳定
桶排序 (bucke sort)	O(N)	O(N)	$O (N^{2})$ or $O (N l o g_{2} N)$	$O (N)$	Out-place	稳定	最坏时间复杂度取决于对于桶内元素进行排序的算法

...

Posted by Wei on 2019-06-25, Last Modified on 2024-01-23

【Algorithm】排序算法 - 冒泡排序（Bubble Sort）

冒泡排序（Bubble Sort）

**冒泡排序（Bubble Sort）**是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行，直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

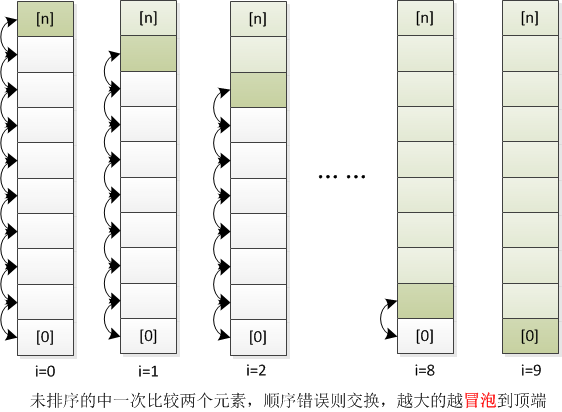
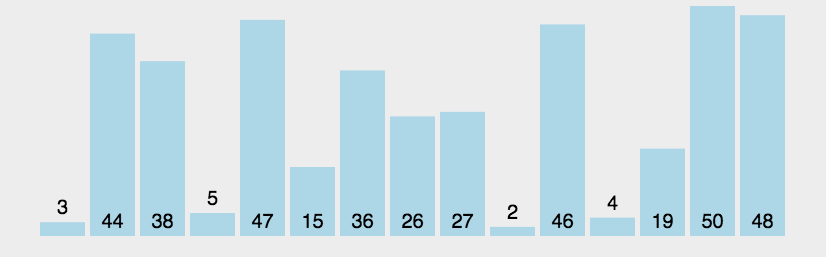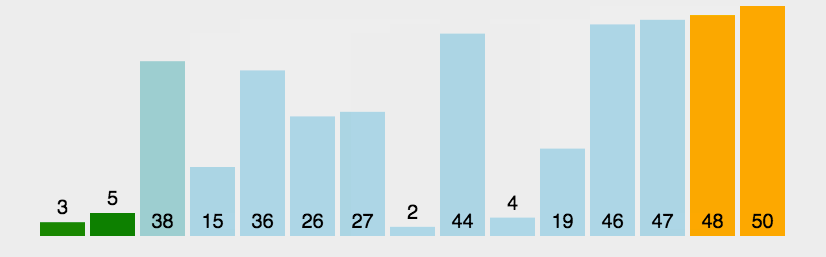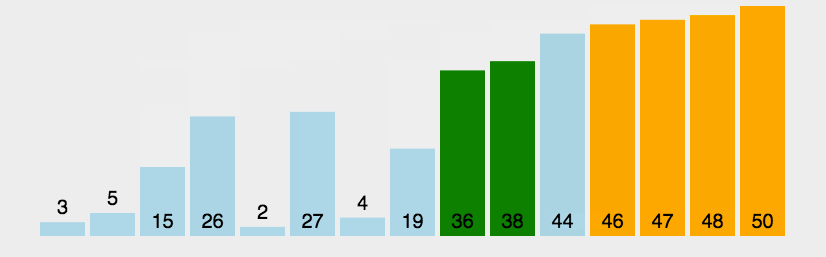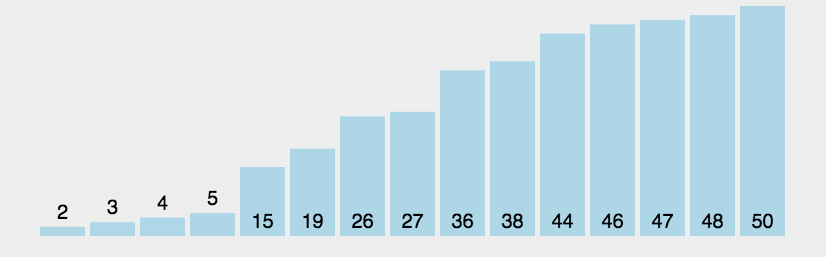
图解冒泡

第一轮冒泡

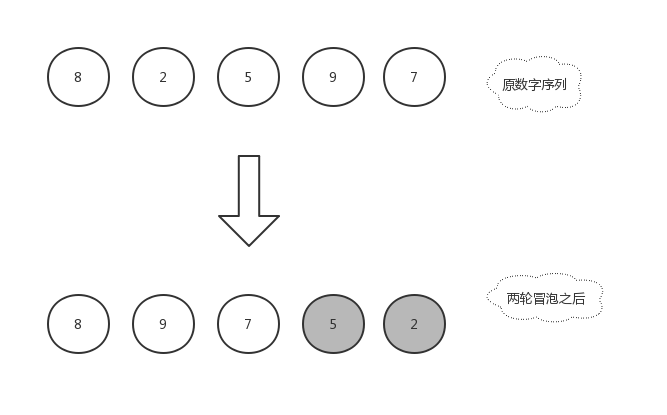
以 [ 8，2，5，9，7 ] 这组数字来做示例。

从左往右依次冒泡，将小的元素往右冒泡（移动）：

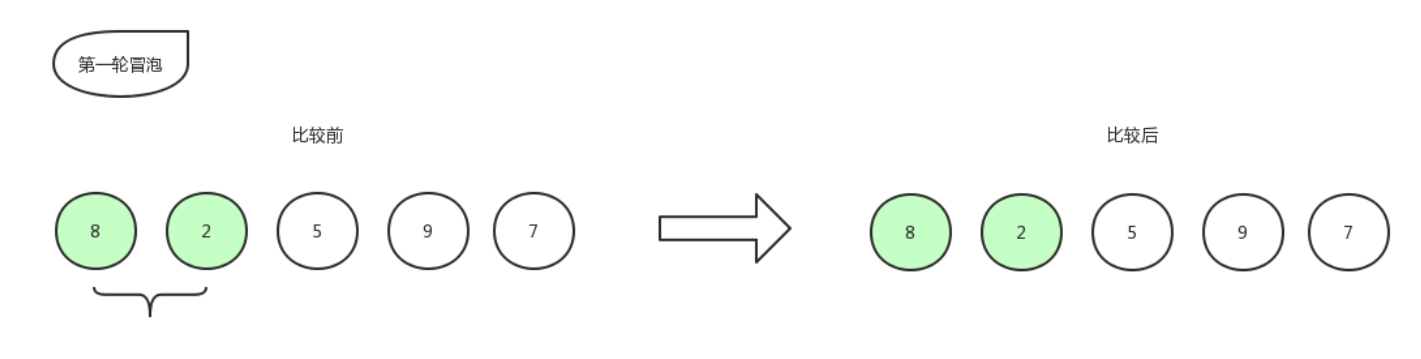
首先比较第一个数和第二个数的大小，我们发现 2 比 8 要小，那么保持原位，不做改动。位置还是 8，2，5，9，7 。

指针往右移动一格，接着比较：

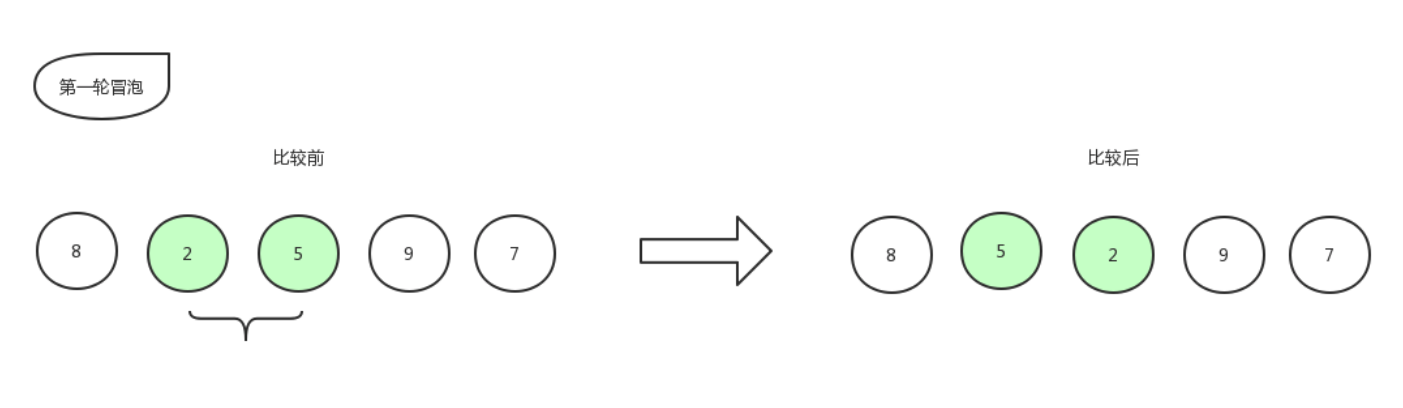
比较第二个数和第三个数的大小，发现 2 比 5 要小，所以位置交换，交换后数组更新为：[ 8，5，2，9，7 ]。

指针再往右移动一格，继续比较：

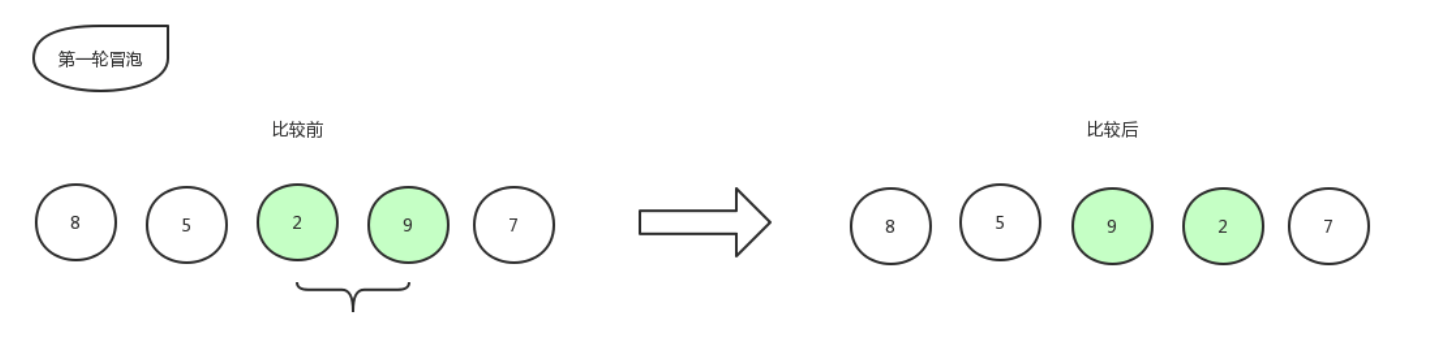
比较第三个数和第四个数的大小，发现 2 比 9 要小，所以位置交换，交换后数组更新为：[ 8，5，9，2，7 ]

同样，指针再往右移动，继续比较：

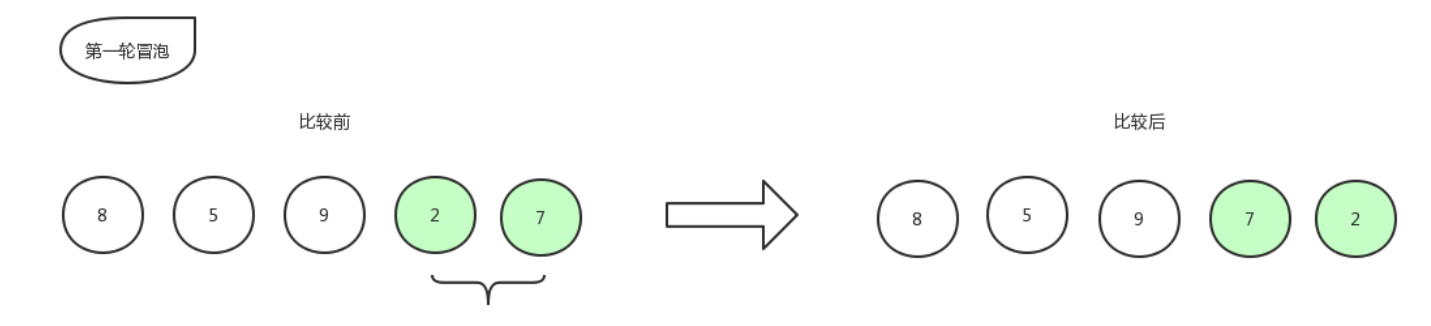
比较第 4 个数和第 5 个数的大小，发现 2 比 7 要小，所以位置交换，交换后数组更新为：[ 8，5，9，7，2 ]

下一步，指针再往右移动，发现已经到底了，则本轮冒泡结束，处于最右边的 2 就是已经排好序的数字。

通过这一轮不断的对比交换，数组中最小的数字移动到了最右边。

第二轮冒泡

接下来继续第二轮冒泡：

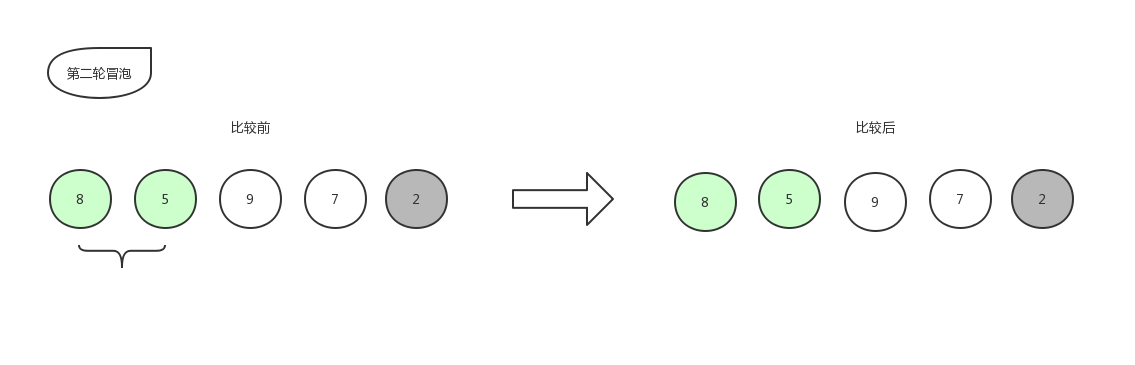
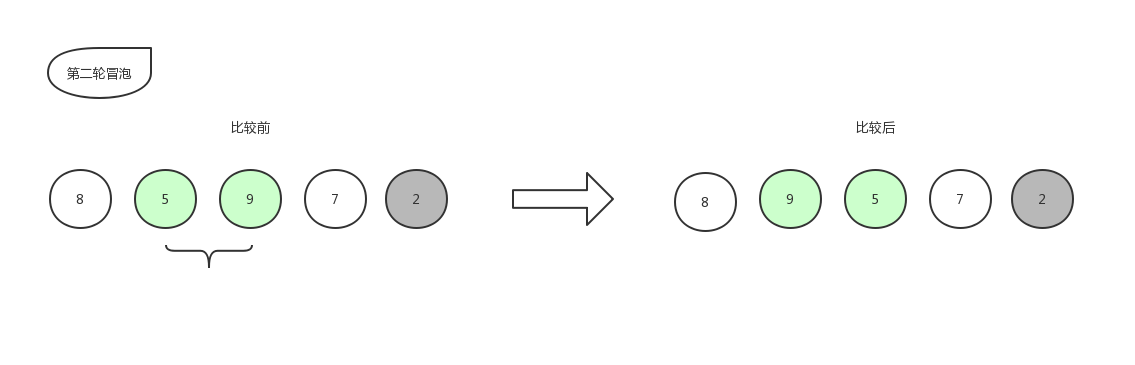
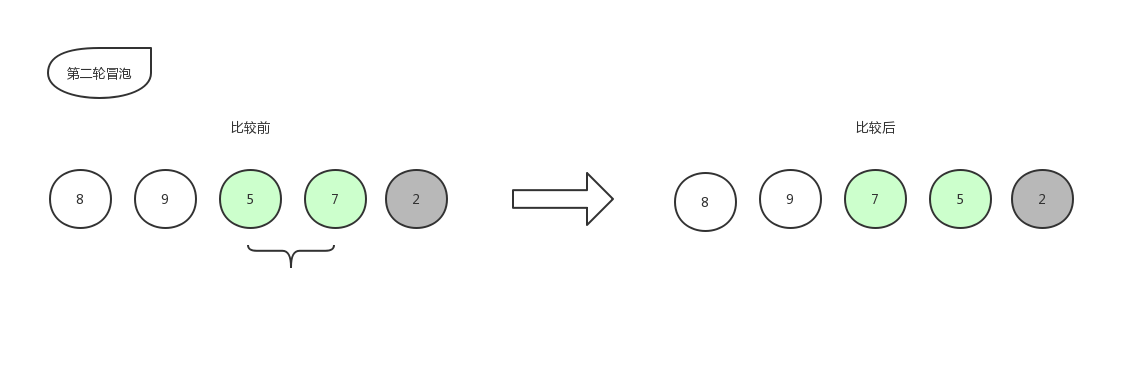
由于右边的 2 已经是排好序的数字，就不再参与比较，所以本轮冒泡结束，本轮冒泡最终冒到顶部的数字 5 也归于有序序列中，现在数组已经变化成了[ 8，9，7，5，2 ]。

第三轮冒泡

让我们开始第三轮冒泡吧！

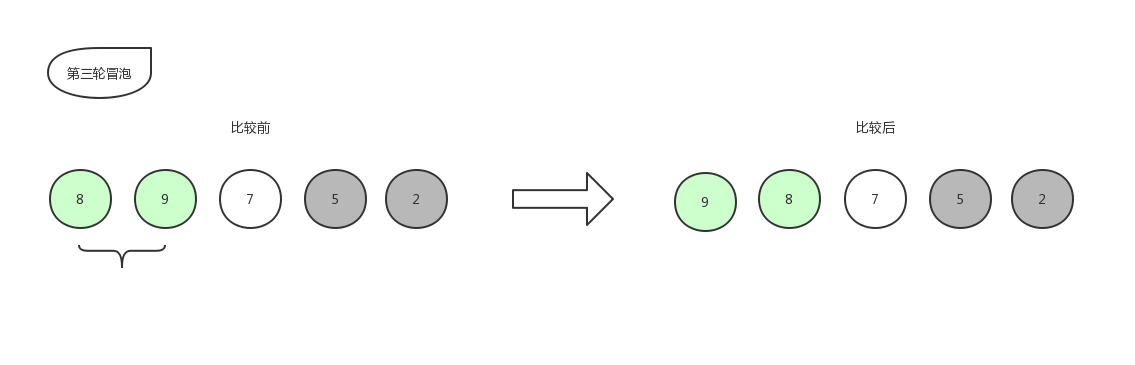
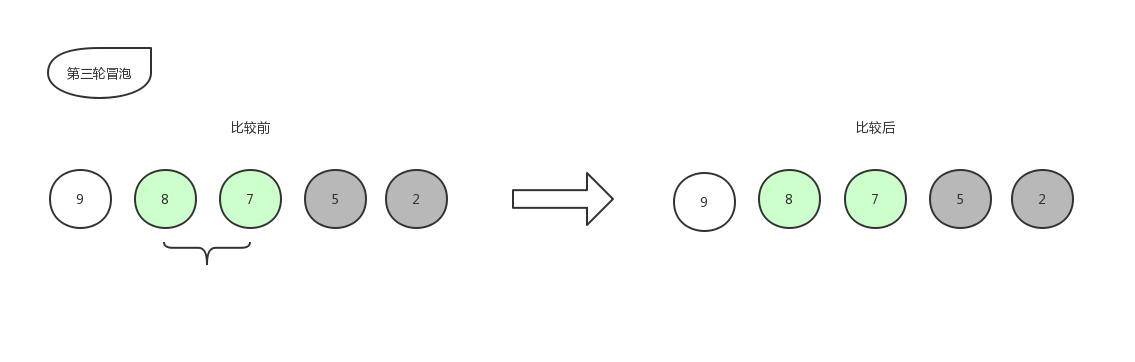
由于 8 比 7 大，所以位置不变，此时第三轮冒泡也已经结束，第三轮冒泡的最后结果是[ 9，8，7，5，2 ]

第四轮冒泡

紧接着第四轮冒泡：

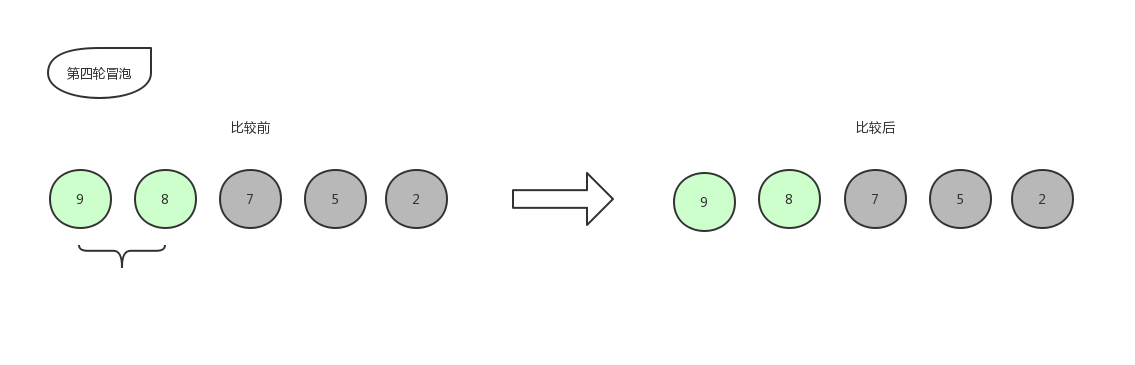
9 和 8 比，位置不变，即确定了 8 进入有序序列，那么最后只剩下一个数字 9 ，放在末尾，自此排序结束。

...

Posted by Wei on 2019-06-25, Last Modified on 2024-01-23

【Algorithm】排序算法 - 快速排序（Quick Sort）

快速排序（Quick Sort）

快速排序的核心思想也是分治法（Divide and Conquer Method），分而治之。

它的实现方式是每次从序列中选出一个基准值（pivot），其他数依次和基准值做比较，比基准值大的放右边，比基准值小的放左边，然后再对左边和右边的两组数分别选出一个基准值，进行同样的比较移动，重复步骤，直到最后都变成单个元素，整个数组就成了有序的序列。

...

Posted by Wei on 2019-06-25, Last Modified on 2024-05-07

【Interview】应聘者提问

SOA

如何看待SOA
下一个SOA

...

Posted by Wei on 2019-06-19, Last Modified on 2024-01-15

【Network】Shadowsocks 总结

Shadowsocks Server

Shadowsocks Server 的实现

shadowsocks: The original Python implementation.

shadowsocks-libev: Lightweight C implementation for embedded devices and low end boxes. Very small footprint (several megabytes) for thousands of connections.

go-shadowsocks2: Another Go implementation focusing on core features and code reusability.

shadowsocks-rust: A rust port of shadowsocks.

shadowsocks-libev

shadowsocks-libev，是一个基于 libev 库开发的 shadowsocks 代理套件。包含ss-local,ss-redir,ss-tunnel,ss-server四部分。
ss-server是shadowsocks 的服务端程序。
ss-local是shadowsocks 客户端程序。
ss-redir是透明代理工具。
ss-tunnel是本地端口转发工具，通常用于解决 dns 污染问题。

...

Posted by Wei on 2019-06-19, Last Modified on 2025-02-25

西维蜀黍