图的顺序存储方法 - 邻接矩阵(Adjacency Matrix)
使用数组存储图时,需要使用两个数组,一个数组存放图中顶点本身的数据(一维数组),另外一个数组用于存储各顶点之间的关系(二维数组)。
- 如果只是存储图中包含的顶点,使用一维数组就足够了;
- 然而,我们还需要存储顶点之间的关系,因此要记录每个顶点和其它所有顶点之间的关系,所以需要使用二维数组。
这个二维数组称为邻接矩阵(Adjacency Matrix)。
不同类型的图,存储的方式略有不同,根据图有无权,可以将图划分为两大类:图和网 。
图,包括无向图和有向图;网,是指带权的图,包括无向网和有向网。
存储方式的不同,指的是:在使用二维数组存储图中顶点之间的关系时,如果顶点之间存在边或弧,在相应位置用 1 表示,反之用 0 表示;如果使用二维数组存储网中顶点之间的关系,顶点之间如果有边或者弧的存在,在数组的相应位置存储其权值;反之用 0 表示。
无向图
我们来看一个无向图的实例,下图的左图就是一个无向图:
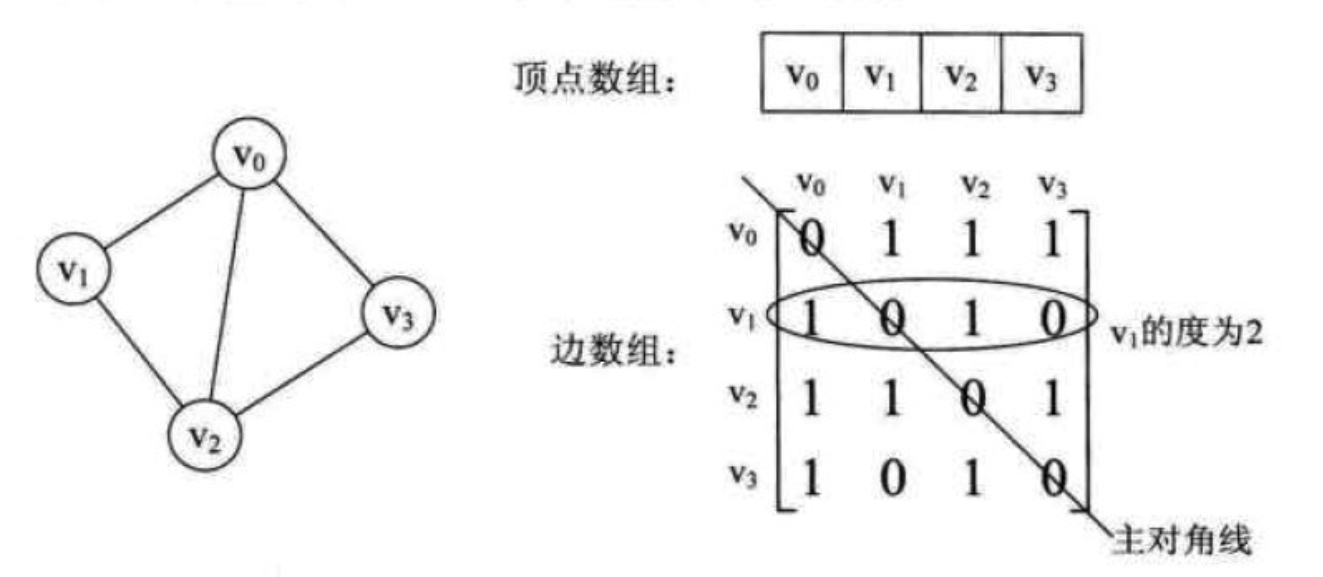
对于无向图来说,二维数组构成的邻接矩阵,实际上是对称矩阵。因此,在存储时就可以采用压缩存储的方式存储下三角或者上三角。
通过二阶矩阵,可以直观地计算出各个顶点的度,为该行(或该列)非 0 值的和。例如,第一行有两个 1,说明 V1 有两个边,所以度为 2。
有向图
我们再来看一个有向图的样例,如下图所示的左图:
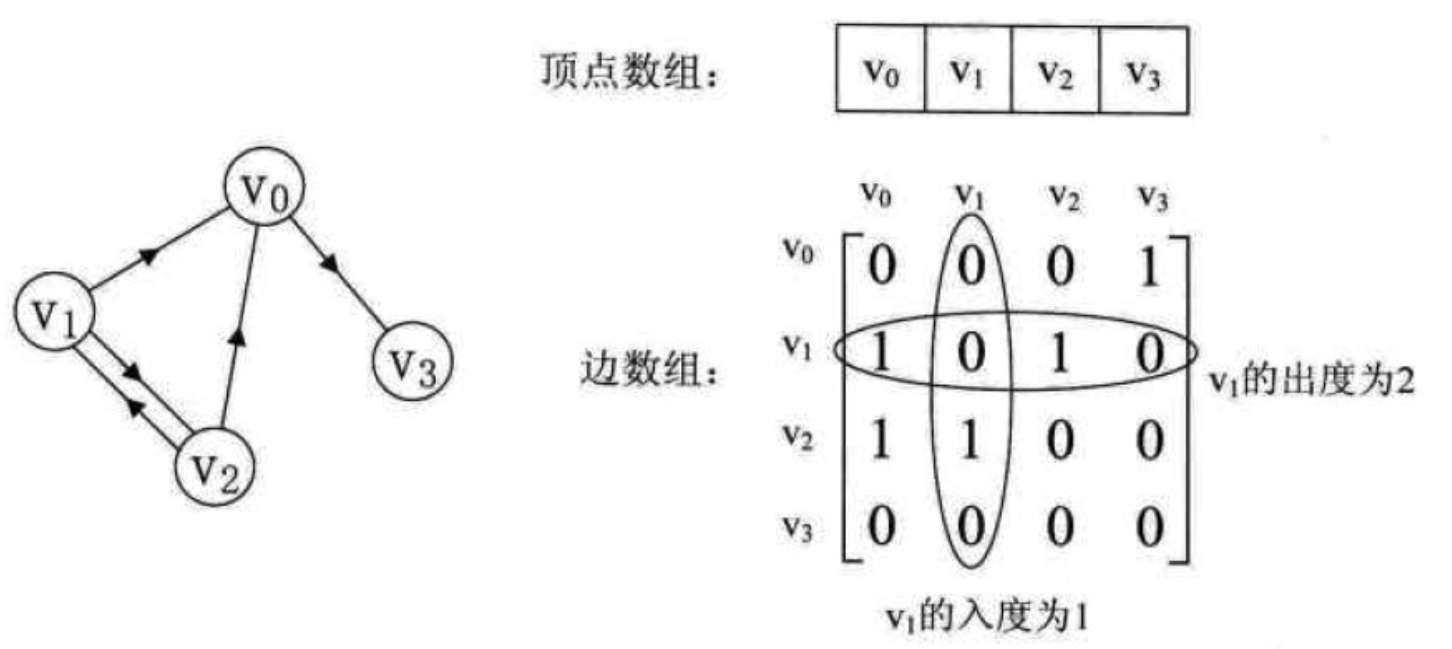
例如,arcs[0][1] = 1 ,证明从 V1 到 V2 有弧存在。且通过邻接矩阵,可以很轻松得知各顶点的出度和入度,出度为该行非 0 值的和,入度为该列非 0 值的和。例如,V1 的出度为 2 (因为第二行中有两个 1 ),为 2 ; V1 的入度为 1 (第二列中只有一个 1 )。
...