背景
**二叉查找树(Binary Search Tree)**在很多情况下可以良好的工作,但它的限制是最坏情况下的时间复杂度为 O(n)。
**平衡二叉查找树(Self-balancing Binary Search Tree)**的设计则是保证其高度在最坏的情况下时间复杂度为 $O(log_2n)$,其插入、删除和查找操作的时间复杂度均为 $O(log_2n)$。常见的平衡二叉查找树包括 AVL树、红黑树。
**多路平衡查找树(Multi-way Self-balancing Search Tree)**作为一般化的平衡二叉查找树(Self-balancing Binary Search Tree),现在其实存在很多种类的平衡查找树,常见的有2-3查找树、2-4查找树、B 树、B+树等。
2-3 树
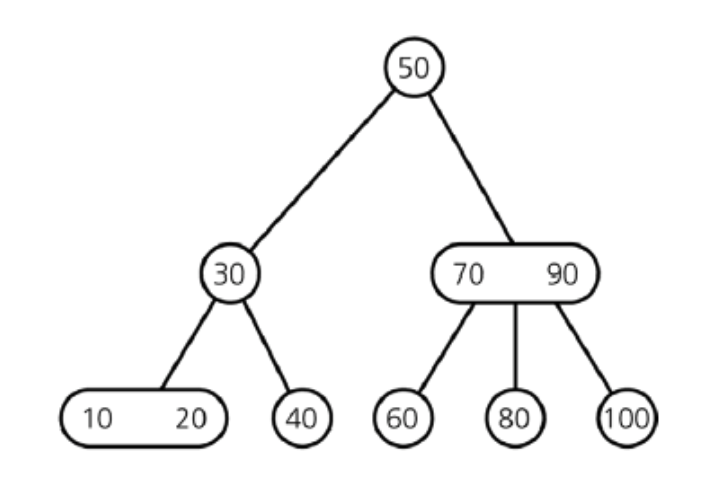
2-3 树中节点和存储的元素符合如下性质要求:
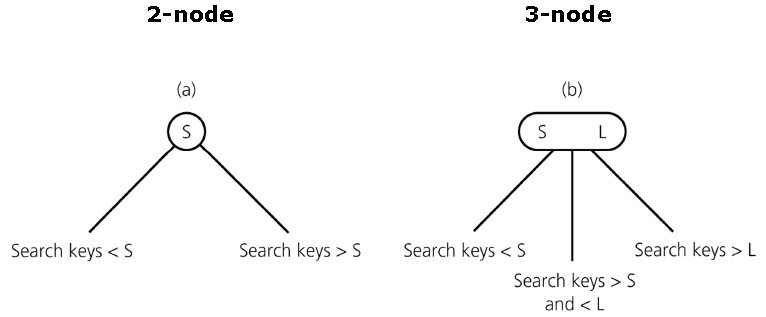
- 任一节点只能是 2 度节点(2-node)或 3 度节点(3-node),不存在值的数量为 0 的节点。
- 2 度节点(2-node):包含 1 个值,且只有 2 个子节点的节点:
- 左子节点子树中所有节点的值都小于这个2 度节点的值;
- 右子节点子树中所有节点的值都大于等于这个2 度节点的值。
- 3 度节点(3-node):包含 2 个值,且只有 3 个子节点的节点:
- 该节点的左值小于右值;
- 左子节点子树中所有节点的值都小于这个 3 度节点的左值;
- 中子节点子树中所有节点的值都大于等于这个 3 度节点的左值,且小于这个 3 度节点的右值;
- 右子节点子树中所有节点的值都大于这个 3 度节点的右值。
- 2 度节点(2-node):包含 1 个值,且只有 2 个子节点的节点:
- 所有叶子节点都拥有相同的深度(depth),或者说,根节点到每一个为空节点的距离都相同。
- 元素始终保持排序顺序。
性能分析
2-3树的查找效率与树的高度是息息相关的。
- 在最坏的情况下,也就是所有的节点都是2-node节点,查找效率为$log_2N$;
- 在最好的情况下,所有的节点都是3-node节点,查找效率为$log_3N$约等于$0.631log_2N$;
距离来说,对于1百万个节点的2-3树,树的高度为12-20之间,对于10亿个节点的2-3树,树的高度为18-30之间。
对于插入来说,只需要常数次操作即可完成,因为他只需要修改与该节点关联的节点即可,不需要检查其他节点,所以效率和查找类似。下面是2-3查找树的效率:
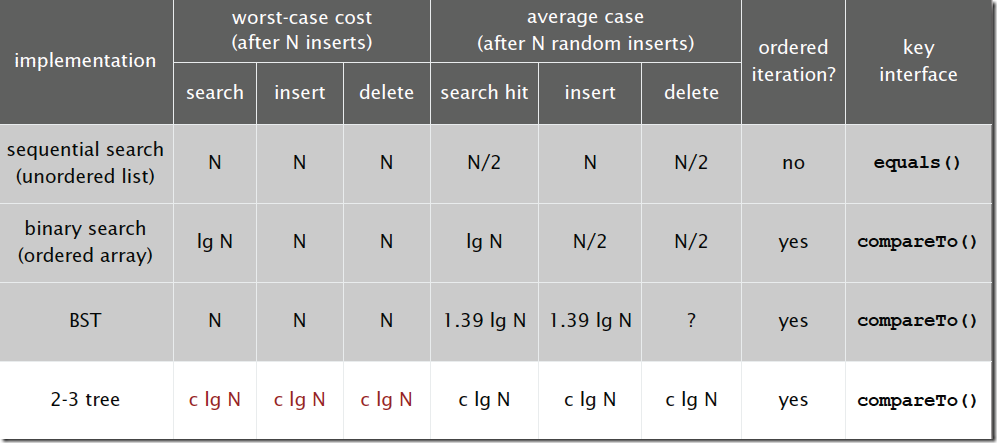
查找操作
在进行2-3树的查找之前,我们先假设已经处于平衡状态。
2-3树的查找和二叉查找树类似,我们首先将待查找值和根节点进行比较,如果相等,则查找成功;否则,往下继续查找,对于只有两个子节点的节点,则在其左右子树中递归查找;而对于有三个子节点的节点,则需要在左中右子树中递归查找。
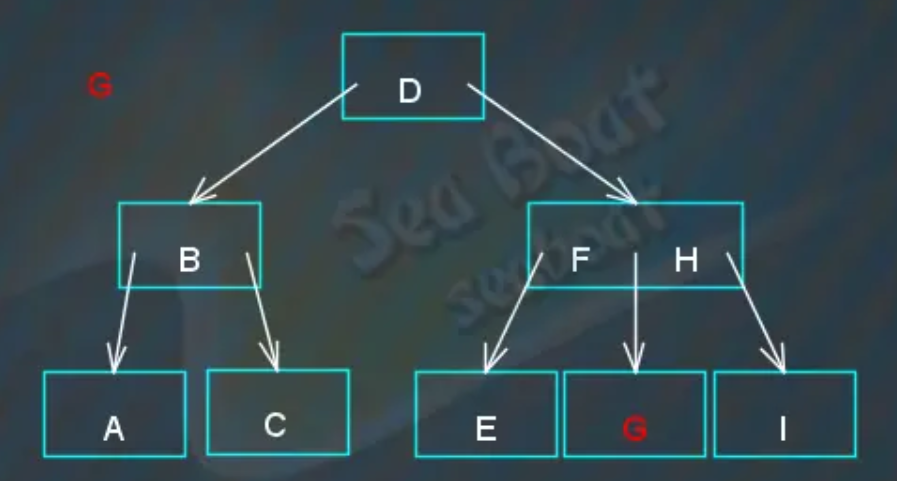
如下2-3树:
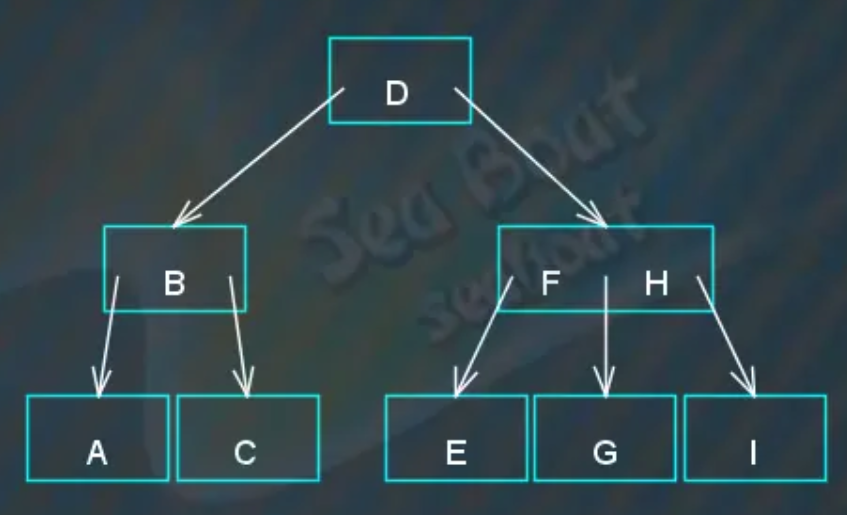
查找“C”节点
从根节点开始,与“D”比较,“C”小于“D”则往左,
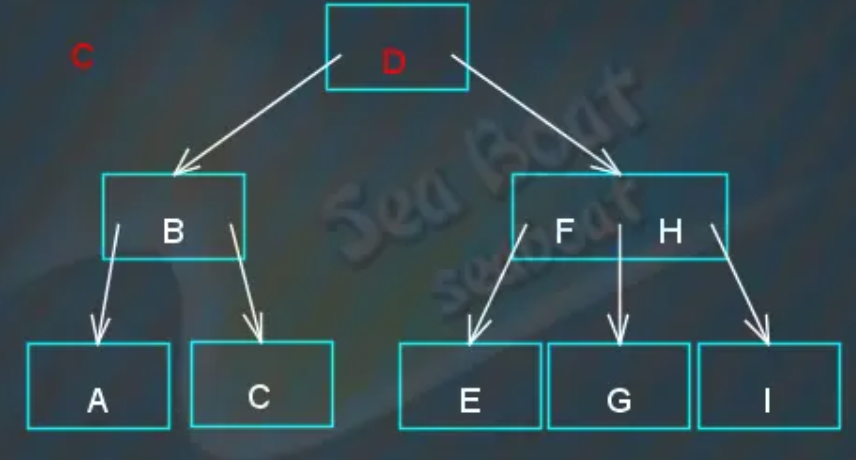
继续与“B”比较,“C”大于“B”则往右,
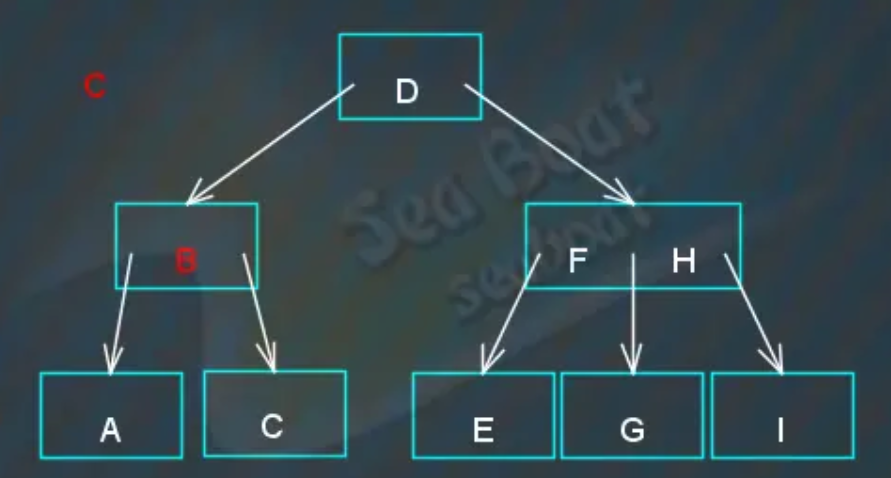
“C”与“C”相等,找到。
查找“H”节点
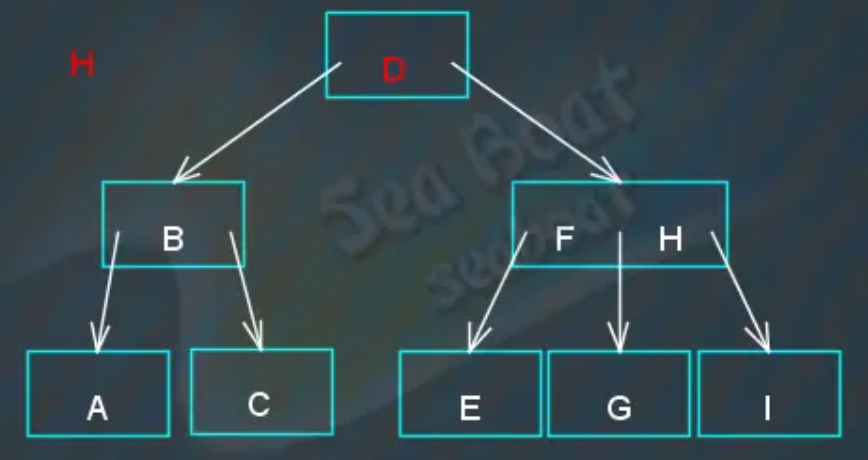
从根节点开始,“H”大于“D”则往右。
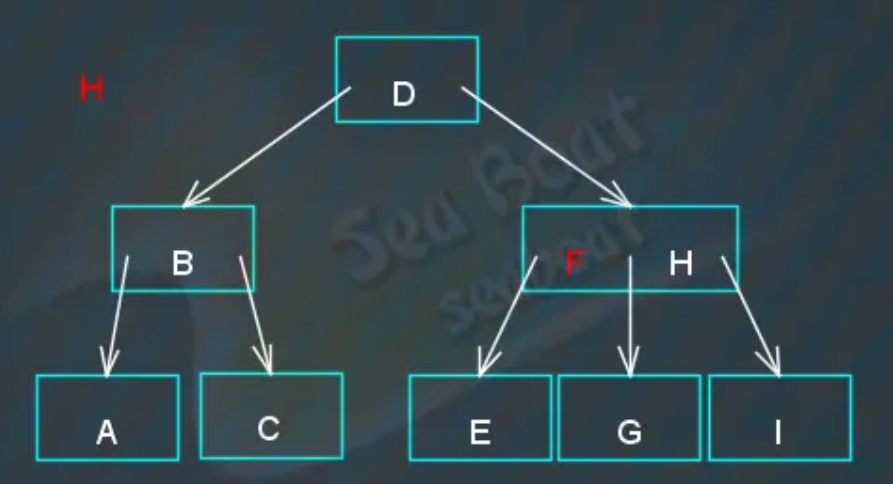
在“FH”节点中逐个项比较,先跟“F”项比较,“H”大于“F”,继续比较下一项,
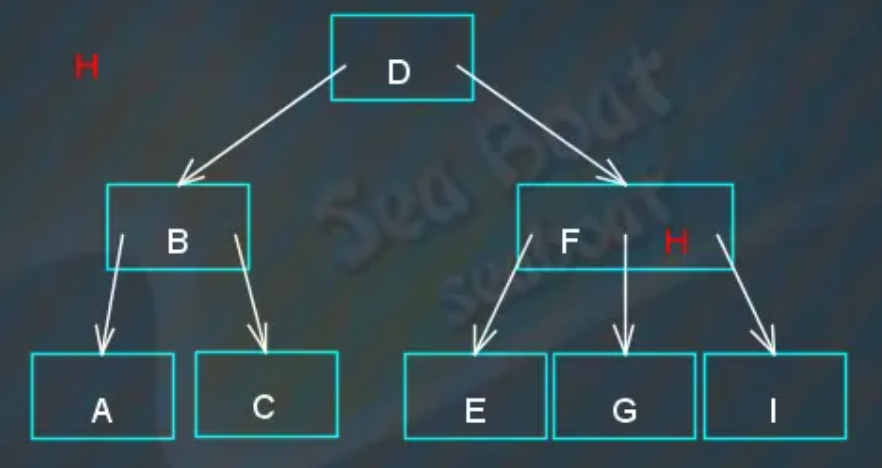
“H”等于“H”,找到,在“FH”节点中找到“H”。
查找“G”节点
从根节点开始,“G”大于“D”则往右:
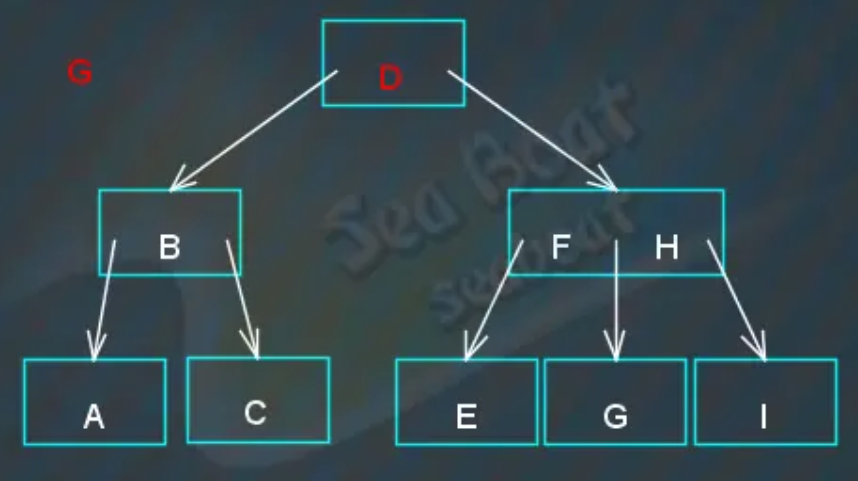
“G”与“FH”节点逐个比较,大于“F”,继续比较下一项:
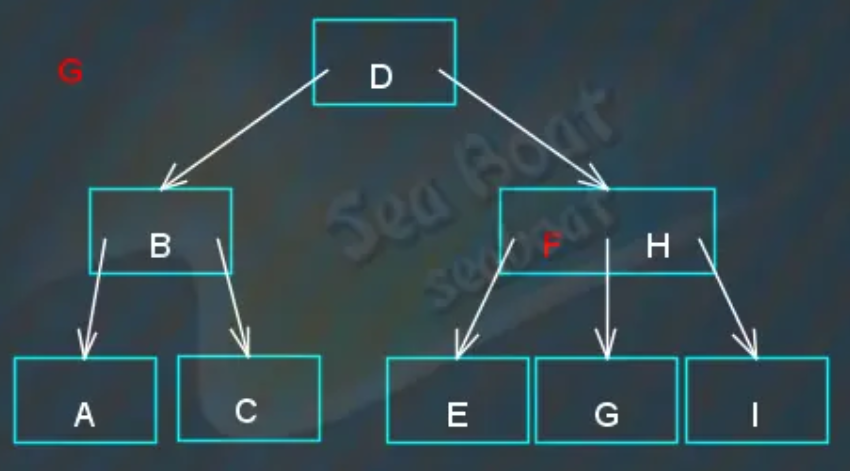
“G”小于“H”,即“G”间于“F”和“H”之间,于是往中间,
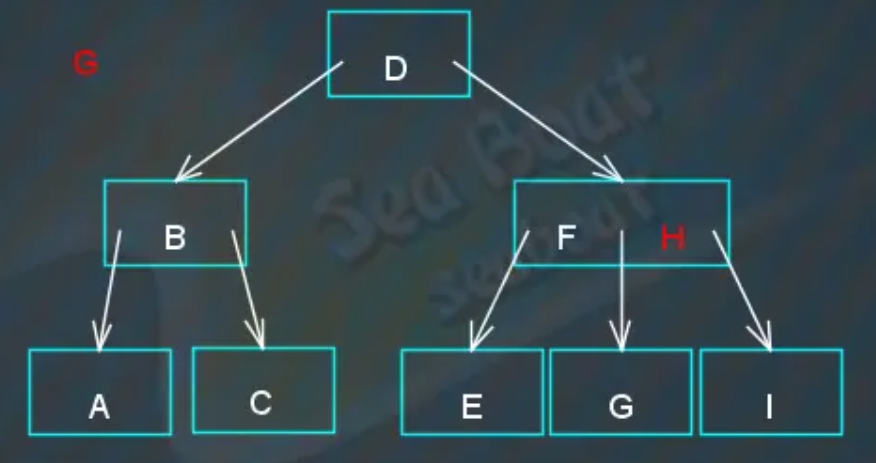
“G”等于“G”,找到。
插入操作
刚开始是空树,插入节点“A”,创建根节点,
插入节点“B”,从根节点开始寻找存放的节点位置,与“A”节点合并后放到同一个叶子上,此时该叶子只包含“AB”两个项目,无需分裂,

继续插入节点“C”,从根节点开始寻找存放的节点位置,找到“AB”叶子节点,将其放进去,
但此时该叶子节点包含了“ABC”三个项目,需要将该节点进行分裂操作,分裂的具体过程如下,找到该节点三个项目中中间大的项,

上移成为最小项和最大项的父节点,而最小项作为中间项的左子节点,最大项作为中间项的右子节点。
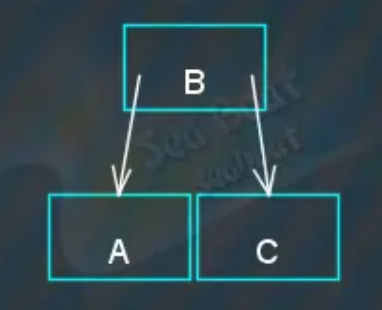
继续插入“D”节点,从根节点开始寻找,
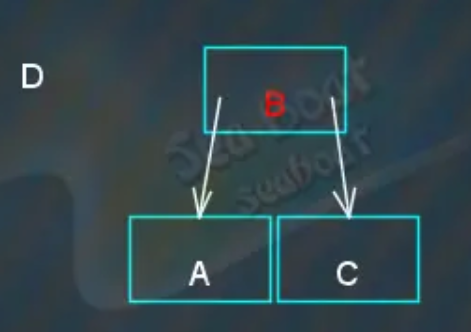
大于“B”,所以往右,
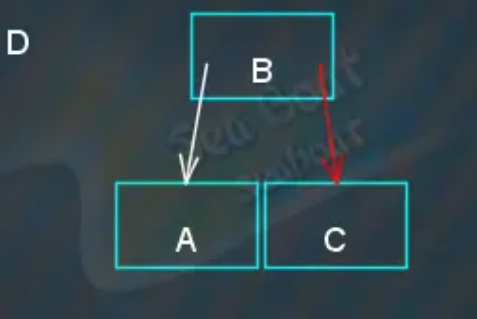
找到“C”节点,并合并到该叶子节点,该节点只有两个项目,不必分裂。
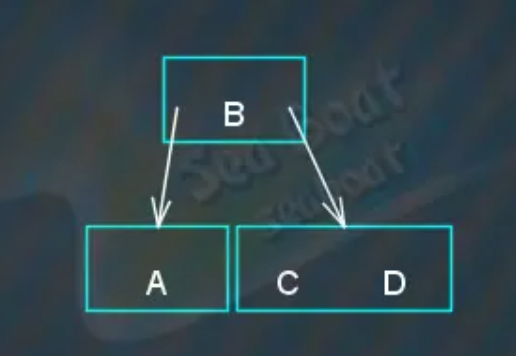
继续插入“E”,查找到“CD”叶子节点,放入“E”节点后发现该叶子节点有三个项目,需要分裂,
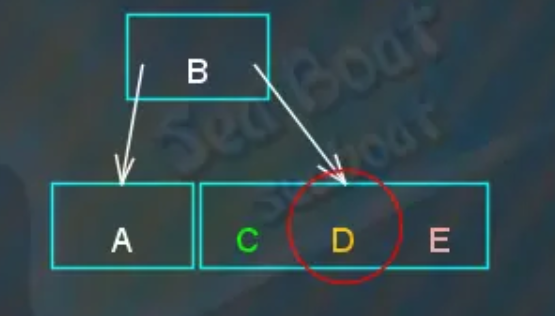
将中间项提升到父节点,其余两项分裂成两个子节点,“D”上升到父节点后存放在右边,而且父节点只有两个项目,不必再继续分裂。
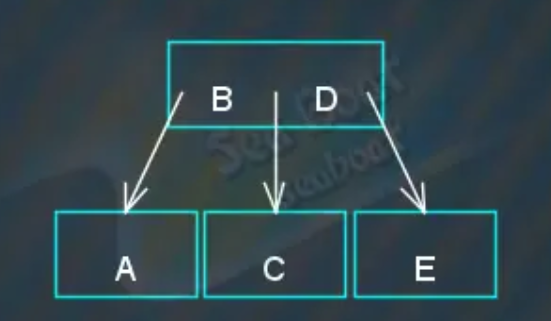
继续插入“F”节点,
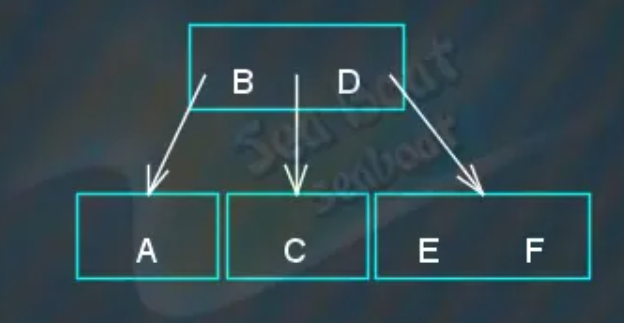
往下看连续分裂两次的情况,继续插入“G”节点,大于“B”,继续比较,
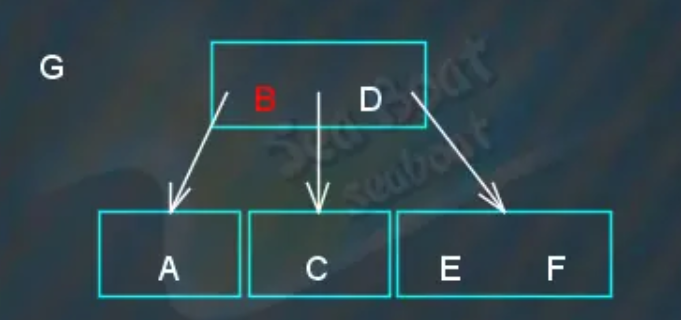
大于“D”,往右子节点,
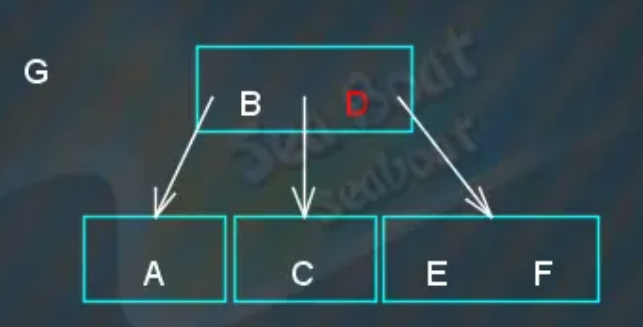
到右子节点后与“F”比较,发现大于“F”,放到右边,
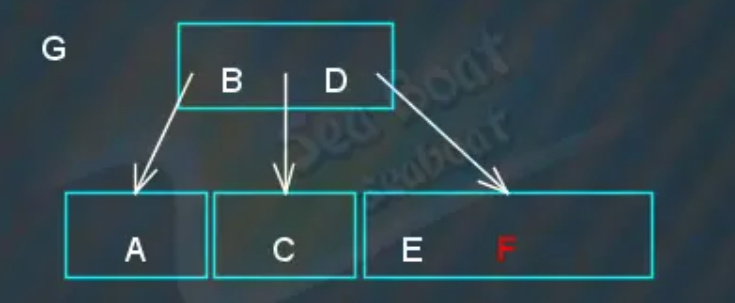
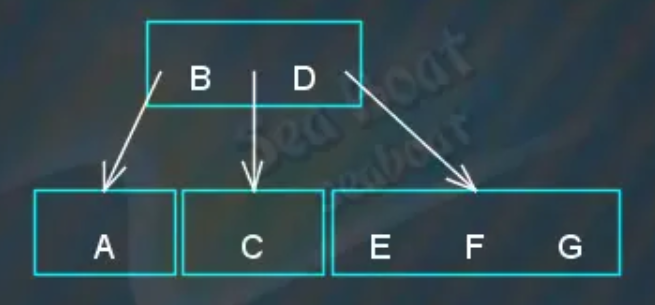
发现“EFG”叶子节点有三个项目,必须分裂,
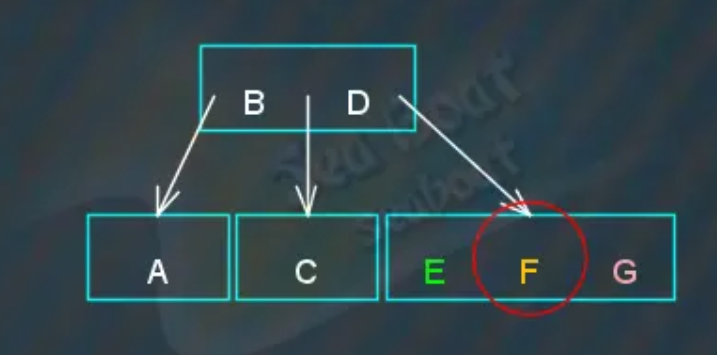
将中间项“F”提升到父节点,“E”和“G”左右两项分别称为左右子节点,
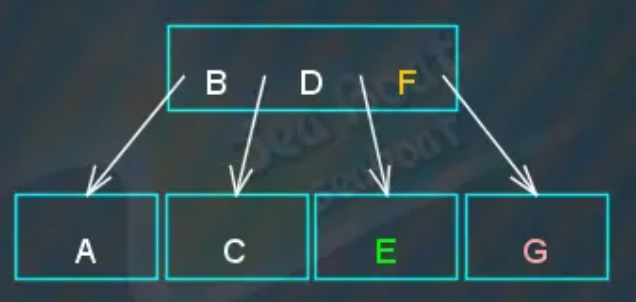
提升到父节点后发现父节点包含了“BDF”三项,也需要分裂,于是准备将中间项“F”提升,
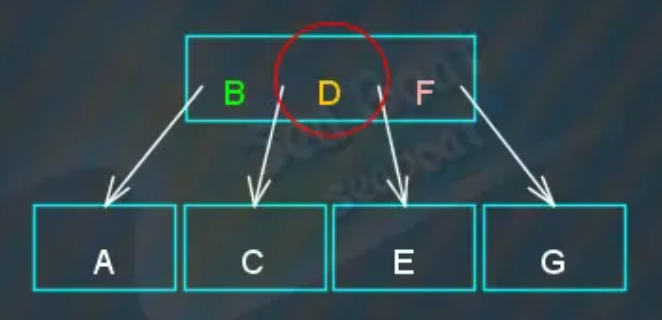
发现“BDF”节点本来属于根节点,那么分裂后就没有根节点了,于是需要创建一个新节点作为根节点,即提升的“D”节点作为新的根节点。“B”和“F”左右两项分别作为左右子节点。
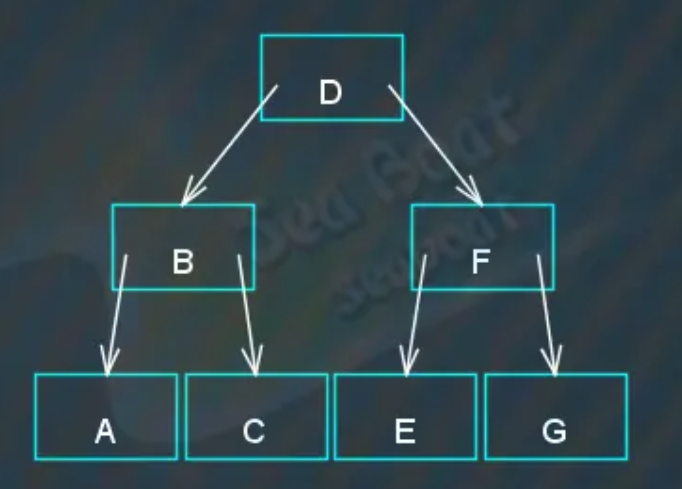
总结起来就是:一个节点插入到一棵2-3树中,先寻找该节点应该落到哪个叶子节点上,注意一定是在叶子节点。将新节点作为一个新项加入到叶子节点中,此时如果该节点只有两个项目,则完成插入操作。但如果该节点有三个项目,则需要进行分裂操作,左中右三项按大小排序,将中间项提升到父节点中,而左右两项作为左右子节点,然后可能还没完,因为父节点上可能又包含了三个项目,如果是这样还得做分裂操作,一直递归到父节点只包含一个或两个项目。
2-3-4 树(2-4 树)
2-3-4 树中节点和存储的元素符合如下性质要求:
- 任一节点只能是 2 度节点、3 度节点或 4 度节点,不存在元素数为 0 的节点。
- 2 度节点:包含 1 个值,且只有 2 个子节点;
- 3 度节点:包含 2 个值,且只有 3 个子节点;
- 4 度节点:包含 3 个值,且只有 4 个子节点;
- 所有叶子节点都拥有相同的深度(depth)。
- 元素始终保持排序顺序。
2 度节点
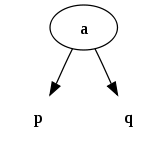
3 度节点
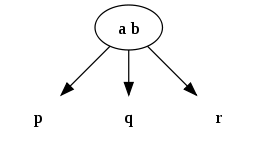
4 度节点
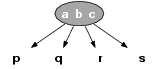
其中,每个子节点仍是一棵 2-3-4 树,但子节点可能为空。
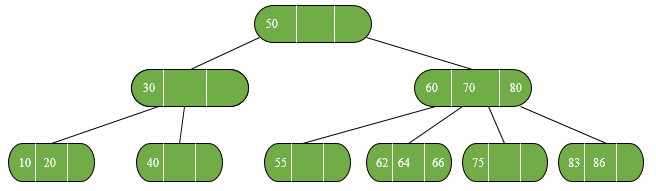
在 2-3-4 树中,所有叶子节点都在同一层,也就是最底层。但是元素却可以出现在所有节点中,也就是说,即使是叶子节点,也可以包含1、2 或 3 个元素,但不能没有元素。2-3-4 树保持着完美的平衡,每一条到叶子节点的路径都是等长的。
非叶子节点必须拥有至少 1 个子节点。设节点的子节点的数量为 L,节点包含元素的数量为 D,则:L = D + 1 。
因为 2-3-4 树中的节点至多包含 4 个子节点,所以该树叶称为 4 阶多路树(multiway tree of order 4)。
操作
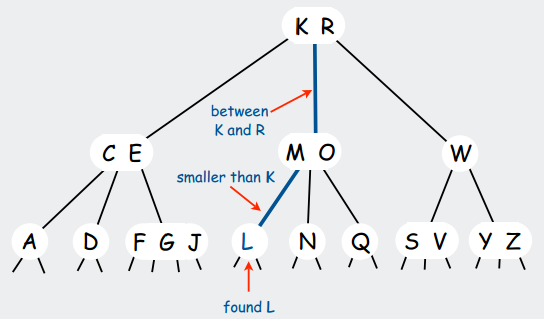
查找操作
在 2-3-4 树中查找结点,分为以下几个步骤:
- 将被查找的元素与节点中存储的元素进行比较;
- 查找包含被查找元素的区间;
- 若区间存在,则移至子节点,回到第 1 步继续查找;
插入操作
插入节点时,将从根节点开始查找,步骤如下:
- 如果当前节点为 4 度节点(也就是有 3 个元素):
- 移除并保存节点中间的元素值,然后生成一个 3 度节点(仅有 2 个元素);
- 将该 3 度节点分裂成一对 2 度节点(仅有 1 个元素);
- 如果当前节点是根节点:
- 被保存的中间值将被设置为新的根节点,该根节点为 2 度节点,则树的高度将增加 1;
- 否则,将中间值加入父节点中。
- 查找子节点中可以包含被插入值的区间;
- 如果找到的节点是一个叶子节点,则将被插入值放入该节点中,插入操作结束;
- 否则,继续查找子节点,或回到步骤 1。
例子
例如,现在要将值 “25” 插入到如下的 2-3-4 树中:
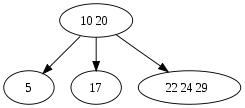
从根节点(10,20)开始查找,向子树查找,直到找到子节点(22,24,29)。因为区间(20,∞)包含 25。
节点(22,24,29)是一个 4 度节点,所以将其中间值 24 推到父节点中。
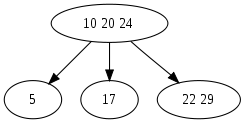
剩下的 3 度节点(22,29)将被分裂成一对 2 度节点,也就是(22)和(29)。新的父节点为(10,20,24)。
在下降到右侧子节点(29)。因为区间(24-29)包含 25。
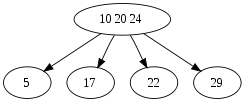
节点(29)没有左孩子。可将 25 直接插入到该节点中,插入完毕。
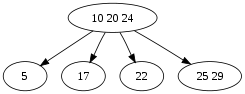
节点的分裂方式
将 4 度节点分裂的方式如下:
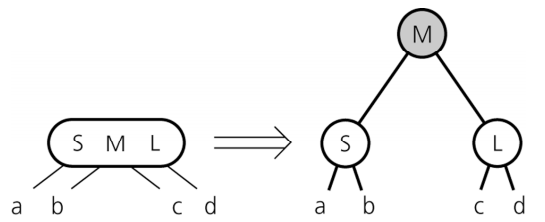
如果一个 4 度节点的父节点是一个 2 度节点,则将按如下方式分裂 4 度节点:
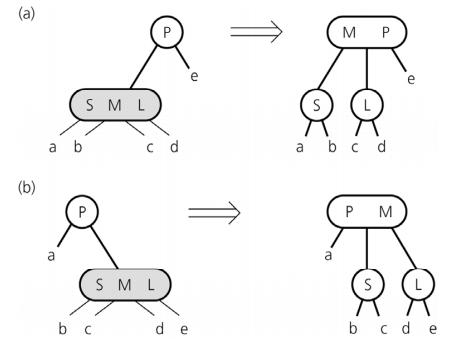
如果一个 4 度节点的父节点是一个 3 度节点,则将按如下方式分裂 4 度节点:
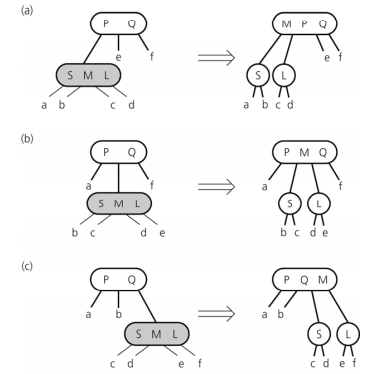
删除节点
情况1:临近兄弟节点是 3 度节点或 4 度节点。
解决方案:通过旋转操作和移动子树来从临近节点偷元素(steal)。
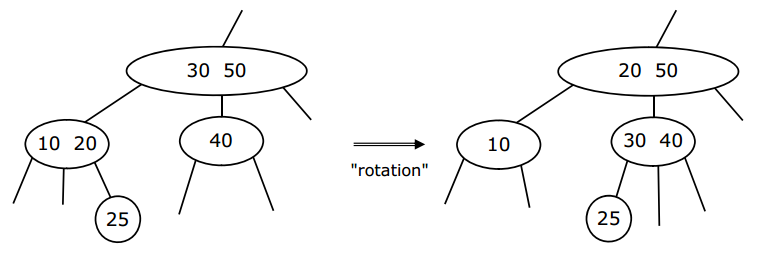
情况2:临近兄弟节点是 2 度节点。
解决方案:通过与临近兄弟节点合并,并从父节点偷元素。
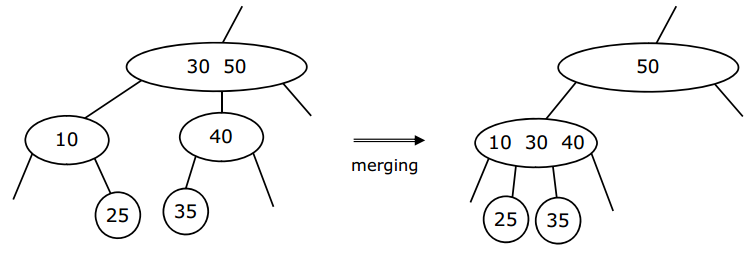
Reference
- 2-3树 - https://zh.wikipedia.org/wiki/2-3%E6%A0%91
- 平衡查找树(2-3-4 树) - https://www.cnblogs.com/gaochundong/p/balanced_search_tree.html
- 浅谈算法和数据结构: 八 平衡查找树之2-3树 - https://www.cnblogs.com/yangecnu/p/Introduce-2-3-Search-Tree.html
- 看图轻松理解数据结构与算法系列(2-3树) - https://juejin.im/post/5b7e00456fb9a01a0b3193c7#heading-4