无处不在的二分思想
二分查找是一种非常简单易懂的快速查找算法，生活中到处可见。比如说，我们现在来做一个猜字游戏。我随机写一个 0 到 99 之间的数字，然后你来猜我写的是什么。猜的过程中，你每猜一次，我就会告诉你猜的大了还是小了，直到猜中为止。你来想想，如何快速猜中我写的数字呢？
假设我写的数字是 23，你可以按照下面的步骤来试一试（如果猜测范围的数字有偶数个，中间数有两个，就选择较小的那个）。
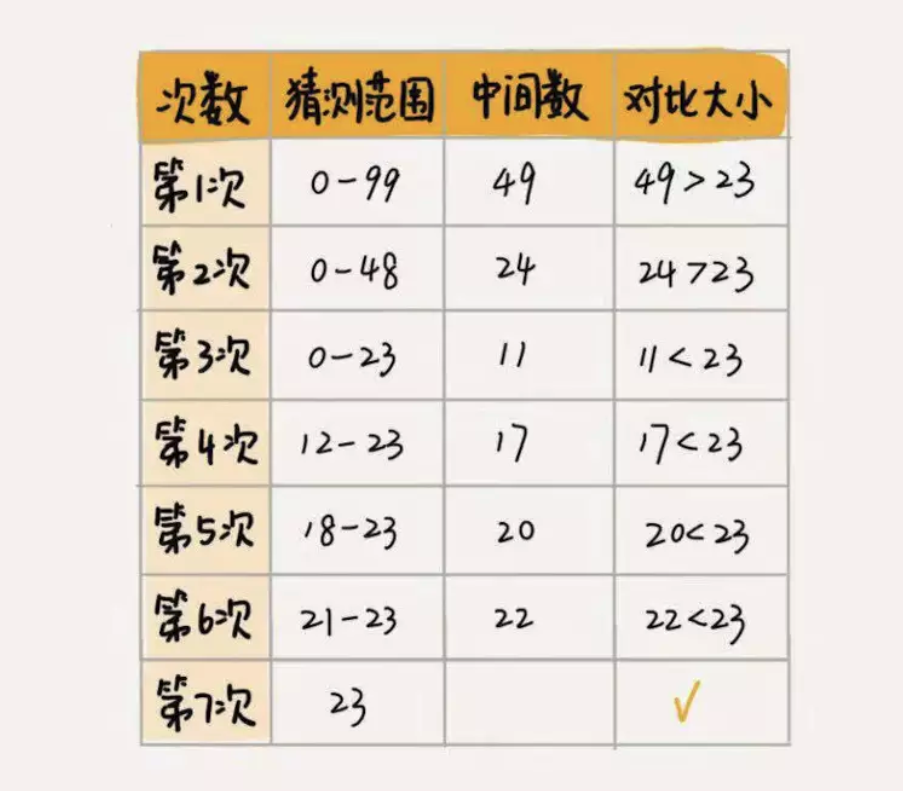
7 次就猜出来了，是不是很快？这个例子用的就是二分思想，按照这个思想，即便我让你猜的是 0 到 999 的数字，最多也只要 10 次就能猜中。不信的话，你可以试一试。
这是一个生活中的例子，我们现在回到实际的开发场景中。假设有 1000 条订单数据，已经按照订单金额从小到大排序，每个订单金额都不同，并且最小单位是元。我们现在想知道是否存在金额等于 19 元的订单。如果存在，则返回订单数据，如果不存在则返回 null。
最简单的办法当然是从第一个订单开始，一个一个遍历这 1000 个订单，直到找到金额等于 19 元的订单为止。但这样查找会比较慢，最坏情况下，可能要遍历完这 1000 条记录才能找到。而使用二分查找就能更快速地解决。
二分搜索算法（binary search）
二分搜索算法（binary search），也称折半搜索（half-interval search）、对数搜索（logarithmic search），是一种在有序数组中查找某一特定元素的搜索算法。
搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
二分搜索在理想情况下的复杂度是对数时间，进行 $O(log_{2}n)$ 次比较操作（n在此处是数组的元素数量，O是大O记号， $log$ 是对数）。二分搜索使用常数空间，无论对任何大小的输入数据，算法使用的空间都是一样的。除非输入数据数量很少，否则二分搜索比线性搜索更快，但数组必须事先被排序。尽管特定的、为了快速搜索而设计的数据结构更有效（比如哈希表），二分搜索应用面更广。
二分搜索有许多中变种。比如分散层叠可以提升在多个数组中对同一个数值的搜索。分散层叠有效的解决了计算几何学和其他领域的许多搜索问题。指数搜索将二分搜索拓宽到无边界的列表。二分查找树和B树数据结构就是基于二分搜索的。
关于二分搜索算法（binary search）
二分搜索算法（binary search）主要是解决在“一堆数中找出指定的数”这类问题。
而想要应用二分搜索算法，这“一堆数”必须有一下特征：
- 存储在数组中
- 有序排列
所以如果是用链表存储的，就无法在其上应用二分查找法了。
至于是顺序递增排列还是递减排列，数组中是否存在相同的元素都不要紧。不过一般情况，我们还是希望并假设数组是递增排列，数组中的元素互不相同。
二分查找法的缺陷
二分查找法的 $O(log_2n)$ 让它成为十分高效的算法。不过，并不是什么情况下都可以用二分查找，它的应用场景有很大局限性。
1 . 二分查找依赖的是顺序表结构，即数组。 二分查找不能依赖于其他数据结构，比如链表。主要原因是二分查找算法需要按照下标随机访问元素。数组按照下标随机访问数据的时间复杂度是 O(1)，而链表随机访问的时间复杂度是 O(n)。所以，如果数据使用链表存储，二分查找的时间复杂就会变得很高。
2 . 二分查找针对的是有序数据。如果数据没有序，需要先排序。排序的时间复杂度最低是 $O(log_2n)$ 。所以，如果针对的是一组静态的数据，没有频繁地插入、删除，就可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低。 针对有频繁插入、删除操作的这种动态数据集合，二分查找是不适用的。要用二分查找，要么每次插入、删除操作之后保证数据仍然有序，要么在每次二分查找之前都先进行排序。针对这种动态数据集合，无论哪种方法，维护有序的成本都很高。
3 . 数据量太小不适合二分查找。如果要处理的数据量很小，完全没有必要用二分查找，顺序遍历就足够了。比如在一个大小为 10 的数组中查找一个元素，不管用二分查找还是顺序遍历，查找速度都差不多。只有数据量比较大的时候，二分查找的优势才会比较明显。
解决这些缺陷问题更好的方法，应该是使用二叉查找树了，最好自然是自平衡二叉查找树了，自能高效的（$O(n log_2n)$）构建有序元素集合，又能如同二分查找法一样快速（$O(log_2n)$）的搜寻目标数。
实现
二分搜索算法在算法家族大类中属于“分治法（Divide and Conquer）”，分治法基本都可以用递归来实现。
Java 递归
public static int binarySearch(int[] arr, int start, int end, int hkey){
if (start > end)
return -1;
int mid = start + (end - start)/2; //防止溢位
if (arr[mid] > hkey)
return binarySearch(arr, start, mid - 1, hkey);
if (arr[mid] < hkey)
return binarySearch(arr, mid + 1, end, hkey);
return mid;
}
注意，为什么这里要用 int mid = start + (end - start)/2;，而不是 mid = (start+end)/2 就好了？
因为，当start 和 end 都很大时（但是在int的value range里面），它们两个加起来就可能会超过2,147,483,647，最终产生溢出的问题。
Java while 循环
public static int binarySearch(int[] arr, int start, int end, int hkey){
int result = -1;
while (start <= end){
int mid = start + (end - start)/2; //防止溢位
if (arr[mid] > hkey)
end = mid - 1;
else if (arr[mid] < hkey)
start = mid + 1;
else {
result = mid;
break;
}
}
return result;
}
Reference
- 二分查找法的实现和应用汇总 - https://www.cnblogs.com/ider/archive/2012/04/01/binary_search.html
- 二分查找 - http://ipine.me/2018-11-08/
- 15 | 二分查找（上）：如何用最省内存的方式实现快速查找功能？ - https://www.jianshu.com/p/78b505a6abf4