Background
介绍动态规划之前先介绍一下分治策略(Divide and Conquer)。
分治策略
将原问题分解为若干个规模较小但类似于原问题的子问题(Divide),「递归」的求解这些子问题(Conquer),然后再合并这些子问题的解来建立原问题的解。
因为在求解大问题时,需要递归的求小问题,因此一般用「递归」的方法实现,即自顶向下。
动态规划(Dynamic Programming)
动态规划其实和分治策略是类似的,也是将一个原问题分解为若干个规模较小的子问题,递归的求解这些子问题,然后合并子问题的解得到原问题的解。 区别在于这些子问题会有重叠,一个子问题在求解后,可能会再次求解,于是我们想到将这些子问题的解存储起来,当下次再次求解这个子问题时,直接拿过来就是。 其实就是说,动态规划所解决的问题是分治策略所解决问题的一个子集,只是这个子集更适合用动态规划来解决从而得到更小的运行时间。
即用动态规划能解决的问题分治策略肯定能解决,只是运行时间长了。因此,分治策略一般用来解决子问题相互对立的问题,称为标准分治,而动态规划用来解决子问题重叠的问题。
将「动态规划」的概念关键点抽离出来描述就是这样的:
- 动态规划法试图只解决每个子问题一次
- 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。
从递归到动态规划
还是以 爬台阶 为例,如果以递归的方式解决的话,那么这种方法的时间复杂度为$O(2^n)$。
背包问题
资源分配型的背包问题是很经典的一类动态规划问题:
- A.我们一个背包装载重量是10,有三个物品,重量分别为5、4、7,价值分别为6、4、9,按照我们的策略先拿价值高的物品,拿了第三个物品后,我们的背包就无法在放入其他物品了。但是我们可以发现如果我们拿第一个和第二个物品,我们可以获得更大的价值。同理也可以举出先拿价值小的策略的反例。
- B.我们一个背包装载重量是10,有三个物品,重量分别为9、4、3,价值分别为1、5、10,按照我们的策略先拿重量高的物品,拿了第一个物品后,我们的背包就无法在放入其他物品了。但是我们可以发现如果我们拿第二个和第三个物品,我们可以获得更大的价值。同理也可以举出先拿重量小的策略的反例。
- 有同学就会有疑问了,我们为什么不按照性价比来拿呢,那么我们来看一下C选项,如果我们一个背包装载重量是10,有三个物品,重量分别为9、4、6,价值分别为20、8、13,我们按照性价比排序,性价比最高的是第一个物品,我们按照策略先拿第一个物品,然后背包不能放入其他物品,其实我们可以发现二三两个物品的价值是超过第一个物品的,我们可以获得更大的价值。同理也可以举出先拿价值小的策略的反例。
这样一个问题,贪心求的只是局部最优解,这一题中无法得到全局最优解,所以我们需要用到动态规划。
动态规划题目特点
- 计数
- 有多少种方式走到右下角
- 有多少种方法选出k个数使得和是Sum
- 求最大最小值
- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度
- 求存在性
- 取石子游戏,先手是否必胜
- 能不能选出k个数使得和是Sum
动态规划组成部分
确定状态
- 状态在动态规划中的作用属于定海神针
- 简单的说,解动态规划的时候需要开一个数组,数组的每个元素f[i]或者 f[i][j]代表什么 – 类似于解数学题中,X,Y,Z代表什么
- 确定状态需要两个意识:
- 最后一步(最优策略中使用的最后一枚硬币aK)
- 子问题(最少的硬币拼出更小的面值27-aK)
转移方程
设状态f[X]=最少用多少枚硬币拼出X。
对于任意X,
初始条件和边界情况
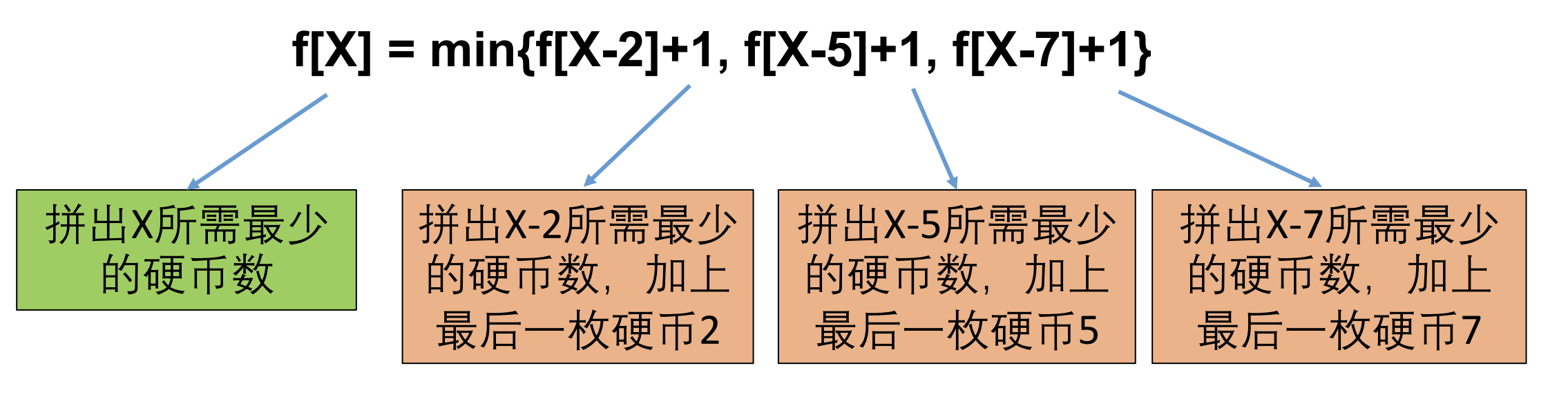
- f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}
- 两个问题:X-2, X-5 或者X-7小于0怎么办?什么时候停下来?
- 如果不能拼出Y,就定义f[Y]=正无穷
- 例如f[-1]=f[-2]=…=正无穷
- 所以f[1] =min{f[-1]+1, f[-4]+1,f[-6]+1}=正无穷, 表示拼不出来1
- 初始条件:f[0] = 0
计算顺序
- 拼出X所需要的最少硬币数:f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}
- 初始条件:f[0] = 0,然后计算f[1], f[2], …, f[27]
- 当我们计算到f[X]时,f[X-2], f[X-5], f[X-7]都已经得到结果了
动态规划题目类型
计数 - 坐标型动态规划
- 最简单的动态规划类型
- 给定一个序列或网格
- 需要找到序列中某个/些子序列或网格中的某条路径
- 某种性质最大/最小
- 计数(有多少种方式走到右下角,有多少种方法选出k个数使得和是Sum)
- 存在性
- 动态规划方程f[i]中的下标i表示以a i 为结尾的满足条件的子序列的性质,f[i][j] 中的下标i, j表示以格子(i, j)为结尾的满足条件的路径的性
- 最大值/最小值
- 个数
- 是否存在
- 坐标型动态规划的初始条件f[0]就是指以a0 为结尾的子序列的性质
例题
- Leetcode - 62 Unique Paths
- Leetcode - 63 Unique Paths II
- Leetcode - 64. Minimum Path Sum
求最大最小值 - 序列型动态规划
- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度
例题
- Leetcode - 322 Coin Change
- LintCode - 515 Paint House
求存在性 - 划分性动态规划
- 取石子游戏,先手是否必胜
- 能不能选出k个数使得和是Sum
例题
- Leetcode - 55 Jump Game
- Lintcode - 512 Decode Ways
Reference
- 看动画轻松理解「递归」与「动态规划」 - https://cxyxiaowu.com/articles/2019/04/04/1554345266086.html