模式匹配/ 字符串匹配算法
字符串匹配
字符串匹配问题的形式定义:
- **文本(Text)**是一个长度为 n 的数组 T[1..n],在下文中,将其对应的字符串称之为"源字符串";
- **模式(Pattern)**是一个长度为 m 且 m≤n 的数组 P[1..m],在下文中,将其对应的字符串称之为"模式字符串";
- T 和 P 中的元素都属于有限的字母表 Σ 表;
- 如果 0≤s≤n-m,并且 T[s+1..s+m] = P[1..m],即对 1≤j≤m,有 T[s+j] = P[j],则说模式 P 在文本 T 中出现且位移为 s,且称 s 是一个有效位移(Valid Shift)。
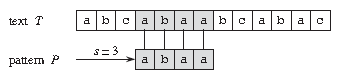
比如上图中,目标是找出所有在文本 T = abcabaabcabac 中模式 P = abaa 的所有出现。该模式在此文本中仅出现一次,即在位移 s = 3 处,位移 s = 3 是有效位移。
常见的字符串匹配算法
解决字符串匹配的算法包括:朴素算法(Naive Algorithm)、Rabin-Karp 算法、有限自动机算法(Finite Automation)、 Knuth-Morris-Pratt 算法(即 KMP Algorithm)、Boyer-Moore 算法、Simon 算法、Colussi 算法、Galil-Giancarlo 算法、Apostolico-Crochemore 算法、Horspool 算法和 Sunday 算法等。
字符串匹配算法的步骤
字符串匹配算法通常分为两个步骤:预处理(Preprocessing)和匹配(Matching)。所以算法的总运行时间为预处理和匹配的时间的总和。
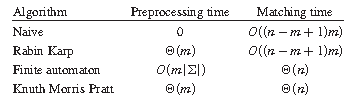
上图描述了常见字符串匹配算法的预处理和匹配时间。
Knuth-Morris-Pratt 字符串匹配算法(即 KMP 算法)
前缀和后缀
在正式介绍KMP 算法之前,我们先解释一下字符串的前缀和后缀的概念。
字符串的前缀(prefix)
如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。例如,”Harry”的前缀包括”H”, ”Ha”, ”Har” 和 ”Harr”。
要注意的是,字符串本身并不是自己的前缀(因为在A=BS中的S,必须是非空字符串)。
字符串的前缀集合
我们把所有前缀组成的集合,称为字符串的前缀集合。例如,”Harry” 的前缀集合为{”H”, ”Ha”, ”Har”, ”Harr”}。
字符串的后缀(postfix)
同样,可以定义后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀。例如,”Potter”的后缀包括”otter”, ”tter”, ”ter”, ”er”, ”r”。
同样地,要注意的是,字符串本身并不是自己的后缀。
字符串的后缀集合
我们把所有后缀组成的集合,称为字符串的后缀集合。例如,”Potter”的后缀集合为{”otter”, ”tter”, ”ter”, ”er”, ”r”}。
注意,字符串的前缀和后缀同样是一个字符串,而前缀集合和后缀集合分别都是一个包含零个到多个字符串的集合。
部分匹配表(Partial Match Table)
对于任何一个非空字符串,我们都可以为之计算出一个对应的部分匹配表(Partial Match Table)。
我们下面来详细讨论一下,如何为一个字符串生成其对应的部分匹配表(Partial Match Table)。至于为什么要生成部分匹配表,我们稍后再解释。
以字符串 “abababca"为例:
char行表示将字符串的各个字符从左向右依次排列的结果;index行的值表示各字符在字符串的索引位置,比如,第一次出现的字符c在字符串 “abababca"中的索引为 6。
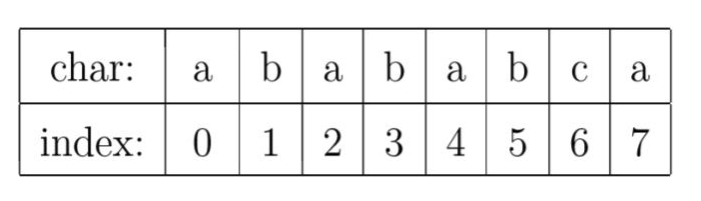
上面的描述很容易理解,我们重点来看看 pmt 行的含义。
首先需要明确的是,pmt 的值,是对于一个字符串而言的(而不是对于一个字符),即字符串的前缀集合与后缀集合的交集中 最长元素的长度值。
例如,对于字符串”aba”,它的前缀集合为{”a”, ”ab”},后缀集合为{”ba”, ”a”}。两个集合的交集为{”a”},那么其中长度最长的元素就是字符串”a”了,其长度为1。所以对于”aba”而言,它在pmt表中对应的值就是1。
再比如,对于字符串”ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3。
回到上面的部分匹配表,我们依次计算字符串 a、ab、aba、abab、ababa、ababab、abababc 和 abababca 的 pmt 值,分别为0、0、1、2、3、4、0和1。在部分匹配表中,我们将这些字符串的pmt值标记为该字符串中最后一个字符的pmt值。比如字符串abababc 的 pmt 值为0,该字符串中的最后一个字符为 c,所以将 0 标记成这个字符 c 的 pmt 值。而事实上,在这个表中,字符 c 的pmt值为 0表示的是字符串 abababc 的 pmt 值 为 0 (pmt 的值,只对一个特定的字符串才有意义)。
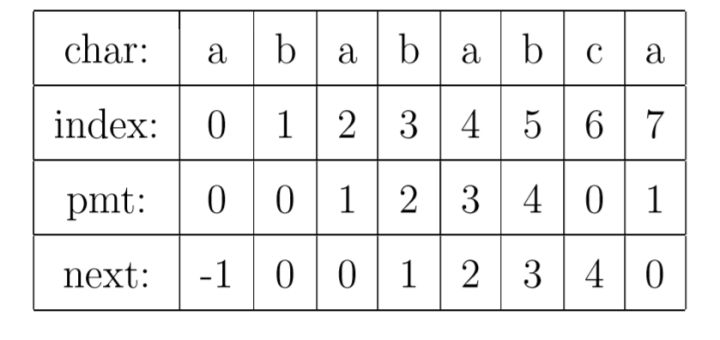
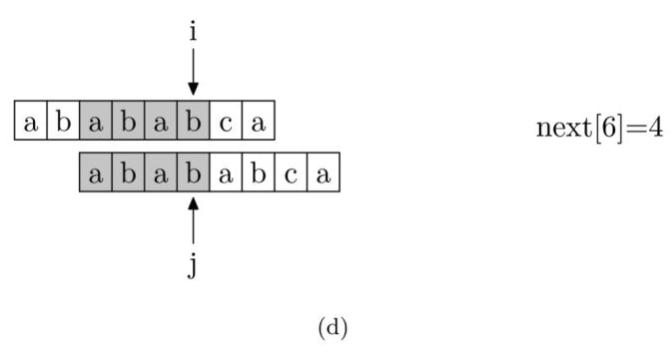
next的值等于当前字符的左边字符的pmt值。比如字符c左边的字符是b,这个字符b的pmt值为4,所以字符c的next值为4。
因为一个字符串的第一个字符的前面不可能有其他字符,所以就不会存在所谓的前后缀相同元素,因此pmt[0]恒等于0。自然地,next[1]恒等于0。
我们还规定next[0]恒等于-1。
演化
KMP 算法本质上是基于朴素的字符串匹配算法(Naive String Matching Algorithm)进行改进的。
因此,我们接下来在回顾朴素的字符串匹配算法之后,指出其不足,并在其基础进行演化。
在朴素的字符串匹配算法(Naive String Matching Algorithm)中,我们首先将串 A (源字符串)与串 B (模式字符串)的首字符对齐,然后逐个判断相对的字符是否相等,如下图所示:

因为字符A与B不匹配,所以模式字符串 “ABCDABD” 右移一个字符,右移后如下所示:

接下来,模式字符串不断右移,直到模式字符串的第一个字符与源字符串中的当前扫描字符相同(情况如下所示):

接着比较模式字符串和源字符串的下一个字符,还是相同(情况如下所示):

直到模式字符串中的当前扫描字符,与源字符串中的当前扫描字符不相同为止(下图描述了不相同的情况):

这时,基于最朴素的字符串匹配思想,我们会继续将模式字符串向右移动一个字符,并将指向模式字符串中字符的指针重置以指向模式字符串的首字符(如下所示)。这样做虽然可行,但是效率很差。

实际上,每当匹配失败时,可以得出两个结论:
- 本趟匹配失败;
- 在模式字符串中,模式字符串当前匹配失败的字符之前的字符串在源字符串中是能够完全匹配成功的,而且在源字符串和模式字符串中的这些匹配字符的位置在这时刚好是一一对应的。
最传统的BF算法正是没有利用第二条结论锁对应的信息,所以效率低。
而KMP算法充分利用了第二条结论的信息,从而尽可能地让模式字符串向右远移。KMP算法的核心思想是尽可能地让模式字符串向右远移,每次匹配失败后模式字符串向右移动越远,比较的次数就会越少,算法的性能自然就提高了。
怎么才能做到这一点呢?这就是理解KMP算法的关键了。
可以针对模式字符串中的每个字符,算出一张部分匹配表(Partial Match Table)。前面,我们已经介绍了如何计算一个字符串对应的部分匹配表。
类似地,我们可以得到字符串 “ABCDABD"的部分匹配表:
| char | A | B | C | D | A | B | D |
|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| pmt | 0 | 0 | 0 | 0 | 1 | 2 | 0 |
回到这个状态:

已知空格与字符 “D” 不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的部分匹配值(pmt值)为2,这意味着字符失配前的字符串(即字符串 ABCDAB )的 pmt 值是 2 。
我们知道,pmt 的值,表示的是字符串的前缀集合与后缀集合的交集中 最长元素的长度值。
对于字符串 ABCDABD,其前缀集合与后缀集合的交集中的最长的元素是字符串 AB,这自然也意味着:字符串 ABCDABD一定以字符串 AB 开头,也一定以字符串 AB 结尾(如下图所示)。注意,这个字符串 ABCDABD既在源字符串中存在,也在模式字符串中存在。
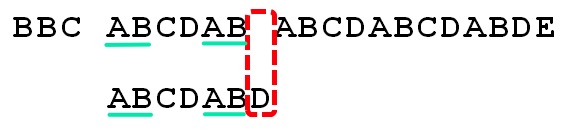
再回顾一次,KMP算法的核心思想是尽可能地让模式字符串向右远移。因此,我们可以将模式字符串右移 4 个字符(因为在模式字符串中,第一次出现的"AB"和第二次出现的"AB"相差4个字符),以使得模式字符串起始部分的"AB"能与源字符串第二次出现的"AB"匹配。你可能会说:这样右移后,即使”AB“相互匹配了,那空格与"C"也不匹配啊?对的,虽然是这样,但是避免了像在最传统的BF算法中,每次只将模式字符串向右一个字符后,就至少做一次比较的情况(这里,KMP是算法右移了4个字符,因此比BF算法在这个过程中,稍进行了三次字符比较)。
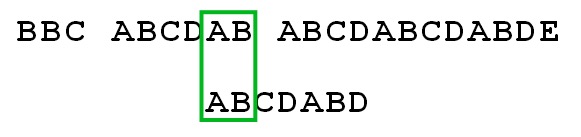
上面的这个分析和右移4个字符的过程,就是基于所谓的"利用当每次匹配失败后,得到的结论2“,即”在模式字符串中,当前匹配失败的字符之前的字符串在源字符串中是能够完全匹配成功的"。
你可能又会想,为什么我们可以直接将模式字符串右移 4 个字符,会不会因此而有漏掉匹配的情况呢?比如假设刚才已经匹配的"ABCDAB"是"ABABAB"的情况,这时候,我们应该只将模式字符串右移 2 个字符。
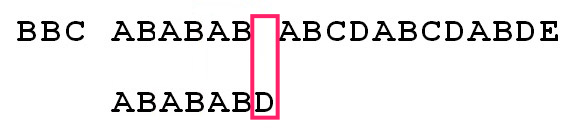
事实上,当模式字符串从"ABCDABD"变成了"ABABABD"后,其对应的部分匹配表也会发生改变:

最后一个匹配字符B对应的部分匹配值(pmt值)为4,这意味着字符失配前的字符串(即字符串 ABABAB )的 pmt 值是 4 。因此,在这种情况下,我们只能把模式字符串右移 2 个字符(因为我们需要具体去判断下面这种场景是不是所有的字符串都匹配了)。
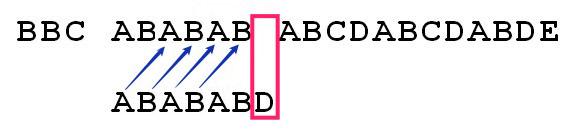
我们发现:
移动位数 = 已匹配的字符数 - 模式字符串最后一个匹配字符的部分匹配值(pmt值)
仔细体会这一点,你就能明白为什么KMP算法要计算部分匹配表(Partial Match Table)了,而且pmt值的计算,是通过计算字符串的前缀集合与后缀集合的交集中 最长元素的长度值来完成。
我们继续回到模式字符串为"ABCDABD"的场景。
因为 6 - 2 等于4,所以将模式字符串向右移动 4 个字符(移动后如下所示):

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2(“AB”),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将模式字符串向右移动 2 个字符。
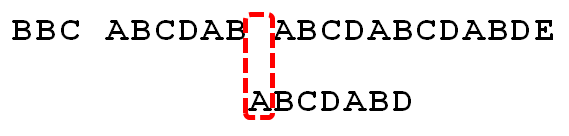
因为空格与A不匹配,继续将模式字符串向右移动 1 个字符。

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将模式字符串向右移动 4 个字符。

逐位比较,直到模式字符串的最后一个字符,发现完全匹配,于是搜索完成。
next数组的计算实现
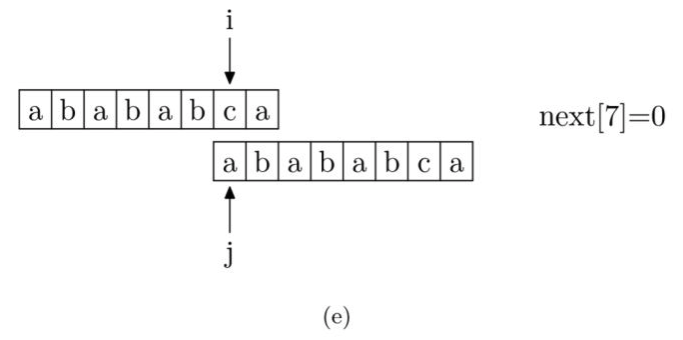
我们来看一下如何编程快速求得next数组。其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为源字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前字符的next值就是匹配成功的字符串的长度。
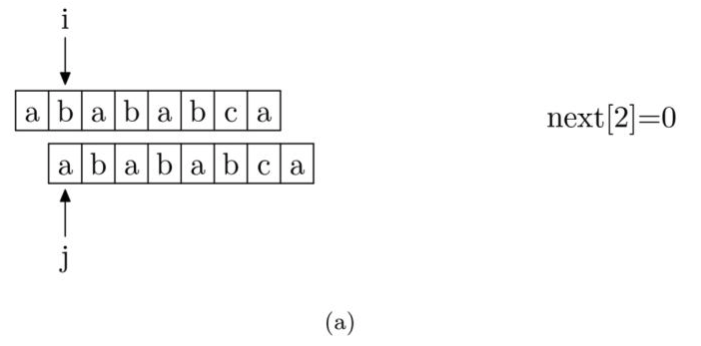
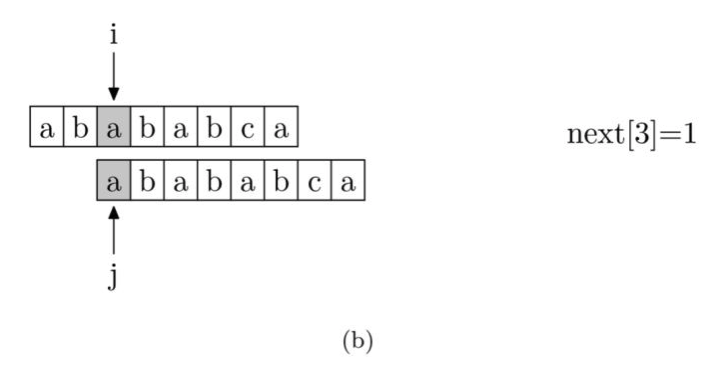
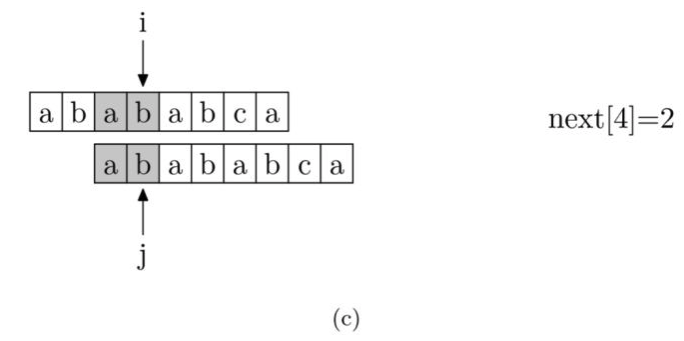
具体来说,从源字符串的索引第1位(而不是第 0 位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前扫描字符的next值。如下图所示。
注意,我们规定next[0] 恒等于 -1,而next[1]一定等于0。
https://juejin.im/post/5b8f9aed6fb9a05d2e1b75d9
https://blog.csdn.net/v_july_v/article/details/7041827
http://www.cnblogs.com/gaochundong/p/boyer_moore_string_matching_algorithm.html
AA 与 AAAAAAAAB
| char | A | A | A | A | A | A | A | A | B |
|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| pmt | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
Java实现
public class KMP {
public int indexOf(String source, String pattern) {
int i = 0, j = 0;
char[] src = source.toCharArray();
char[] ptn = pattern.toCharArray();
int sLen = src.length;
int pLen = ptn.length;
int[] next = getNext(ptn);
while (i < sLen && j < pLen) {
// 如果j = -1,或者当前字符匹配成功(src[i] = ptn[j]),都让i++,j++
if (j == -1 || src[i] == ptn[j]) {
i++;
j++;
} else {
// 如果j!=-1且当前字符匹配失败,则令i不变,j=next[j],即让pattern模式串右移j-next[j]个单位
j = next[j];
}
}
if (j == pLen)
return i - j;
return -1;
}
public int[] getNext(char[] p) {
// 已知next[i] = j,利用递归的思想求出next[i+1]的值
// 如果已知next[i] = j,如何求出next[i+1]呢?具体算法如下:
// 1. 如果p[i] = p[j], 则next[i+1] = next[j] + 1;
// 2. 如果p[i] != p[j], 则令j=next[j],如果此时p[i]==p[j],则next[i+1]=j+1,
// 如果不相等,则继续递归前缀索引,令 j=next[j],继续判断,直至j=-1(即j=next[0])或者p[i]=p[j]为止
int pLen = p.length;
int[] next = new int[pLen];
next[0] = -1; // next数组中next[0]为-1
int j = -1;
int i = 0;
while (i < pLen - 1) {
if (j == -1 || p[i] == p[j]) {
j++;
i++;
next[i] = j;
} else {
j = next[j];
}
}
return next;
}
}
public static void main(String[] args){
KMP kmp = new KMP();
String a = "QWERQWR";
String b = "WWE QWERQW QWERQWERQWRT";
int[] next = kmp.getNext(a.toCharArray());
for(int i = 0; i < next.length; i++){
System.out.println(a.charAt(i)+" "+next[i]);
}
int res = kmp.indexOf(b, a);
System.out.println(res);
}
总结
预处理过程(COMPUTE-PREFIX-FUNCTION)的运行时间为 Θ(m),KMP-MATCHER 的匹配时间为 Θ(n)。
相比较于朴素的字符串匹配算法(Naive String Matching Algorithm),KMP算法的主要优化点就是在当确定字符不匹配时对于 pattern 的位移。
假设主串S的长度为n,模式串P的长度为m。
KMP 算法的主要特点是:
- 需要对模式字符串做预处理;
- 预处理阶段需要额外的 O(m) 空间和复杂度;
- 匹配阶段与字符集的大小无关;
- 匹配阶段至多执行 2n - 1 次字符比较;
- 对模式中字符的比较顺序时从左到右;
Reference
- 数据结构-串 - https://zhuanlan.zhihu.com/p/29160321
- 数据结构之串 - https://www.zybuluo.com/guoxs/note/237408
- [数据结构]线性结构——串 - https://blog.csdn.net/shimazhuge/article/details/46808193
- 字符串匹配算法 - https://www.cnblogs.com/gaochundong/p/string_matching.html
- 字符串匹配的KMP算法 - http://www.ruanyifeng.com/blog/2013/05/Knuth–Morris–Pratt_algorithm.html
- 字符串匹配算法 - https://www.cnblogs.com/gaochundong/p/string_matching.html
- 算法之字符串模式匹配 - https://zhuanlan.zhihu.com/p/24649304
- KMP算法之java实现 - https://blog.csdn.net/roy_70/article/details/78330246
- 如何更好的理解和掌握 KMP 算法? - https://www.zhihu.com/question/21923021