递归（Recursion）
先下定义：递归算法是一种直接或者间接调用自身函数或者方法的算法。
通俗来说，递归算法的实质是把问题分解成规模缩小的同类问题的子问题，然后递归调用方法来表示问题的解。它有如下特点：
- 一个问题的解可以分解为几个子问题的解
- 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
- 存在递归终止条件，即必须有一个明确的递归结束条件，称之为递归出口
理解
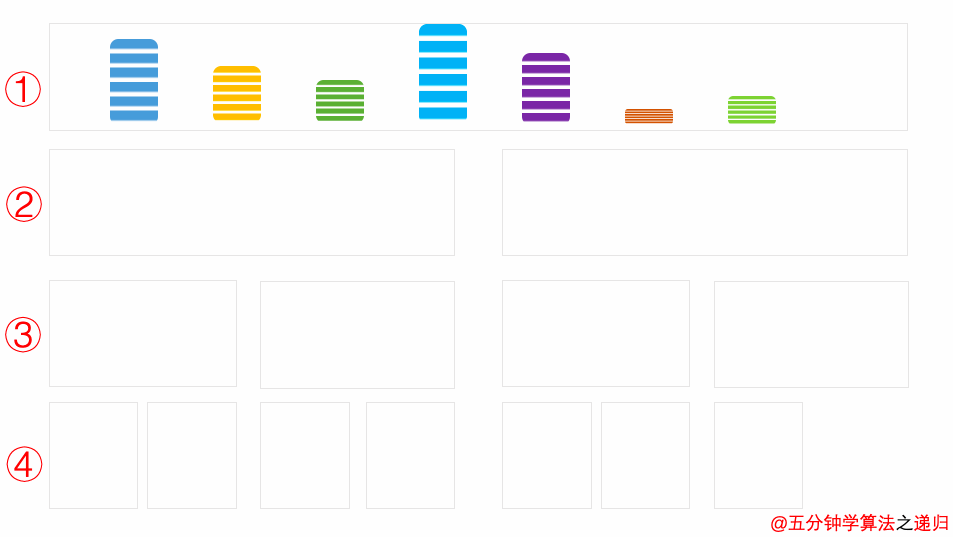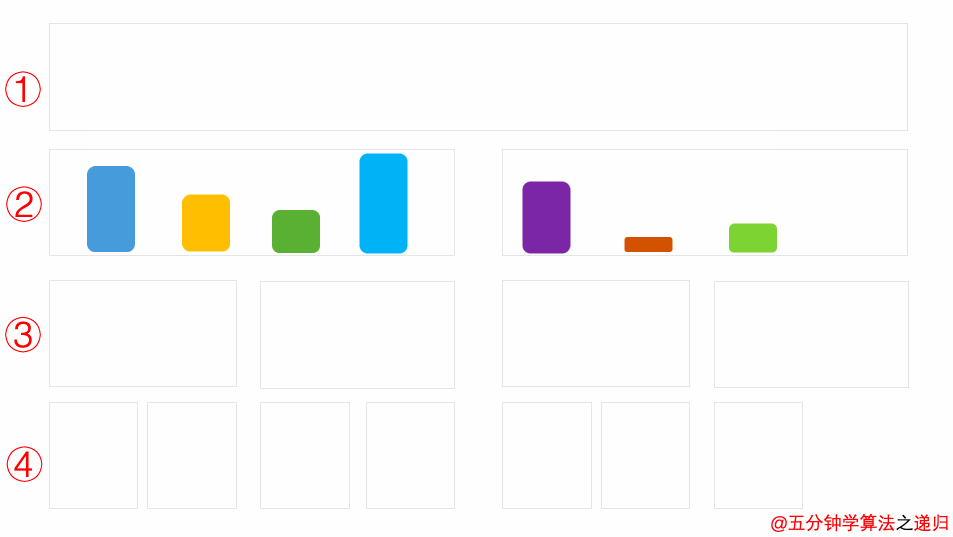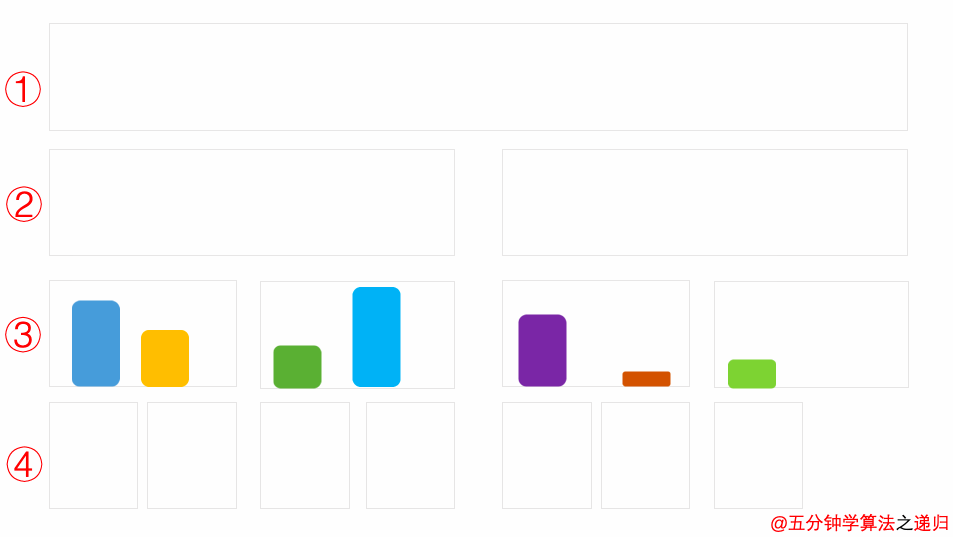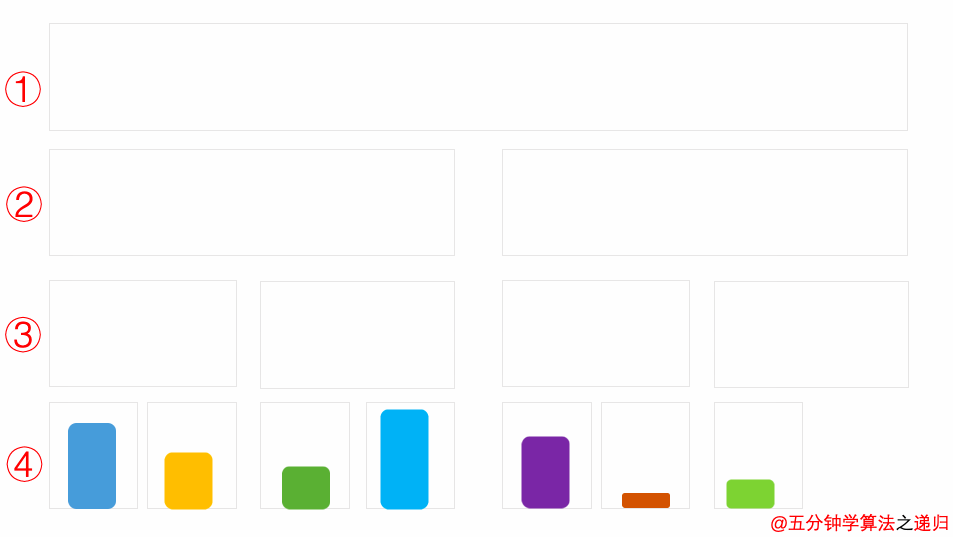
通过动画一个一个特点来进行分析。
1 一个问题的解可以分解为几个子问题的解
子问题就是相对与其前面的问题数据规模更小的问题。
在动图中①号问题（一块大区域）划分为②号问题，②号问题由两个子问题（两块中区域）组成。
2 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
「①号划分为②号」与「②号划分为③号」的逻辑是一致的，求解思路是一样的。
3 存在递归终止条件，即存在递归出口
把问题分解为子问题，把子问题再分解为子子问题，一层一层分解下去，不能存在无限循环，这就需要有终止条件。
①号划分为②号，②号划分为③号，③号划分为④号，划分到④号的时候每个区域只有一个不能划分的问题，这就表明存在递归终止条件。
经典递归示例
1 数组求和
Sum(arr[0...n-1]) = arr[0] + Sum(arr[1...n-1])
后面的 Sum 函数要解决的就是比前一个 Sum 更小的同一问题。
Sum(arr[1...n-1]) = arr[1] + Sum(arr[2...n-1])
以此类推，直到对一个空数组求和，空数组和为 0 ，此时变成了最基本的问题。
Sum(arr[n-1...n-1] ) = arr[n-1] + Sum([])
2 汉诺塔（Hanoi Tower）问题
汉诺塔（Hanoi Tower）问题也是一个经典的递归问题，该问题描述如下：
汉诺塔问题：古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上。有一个和尚想把这个盘子从A座移到B座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。
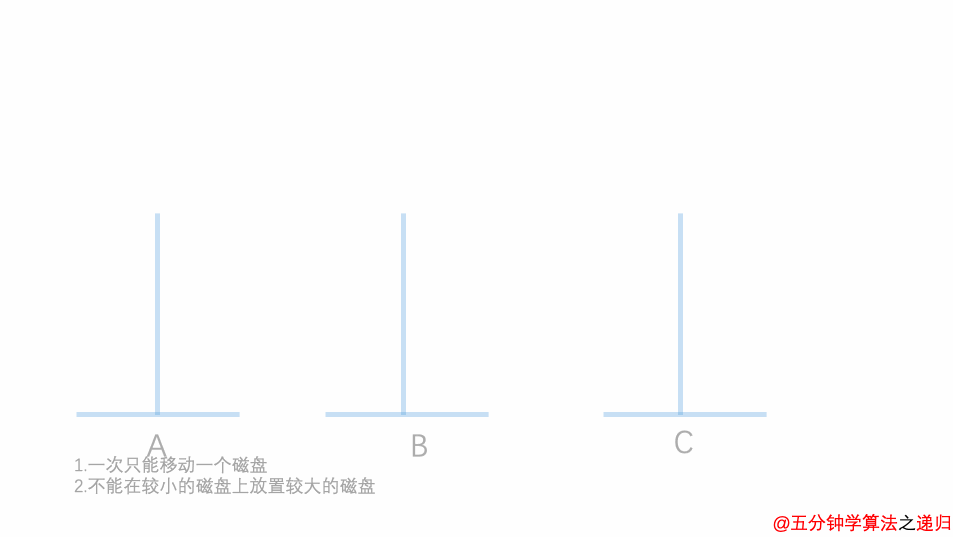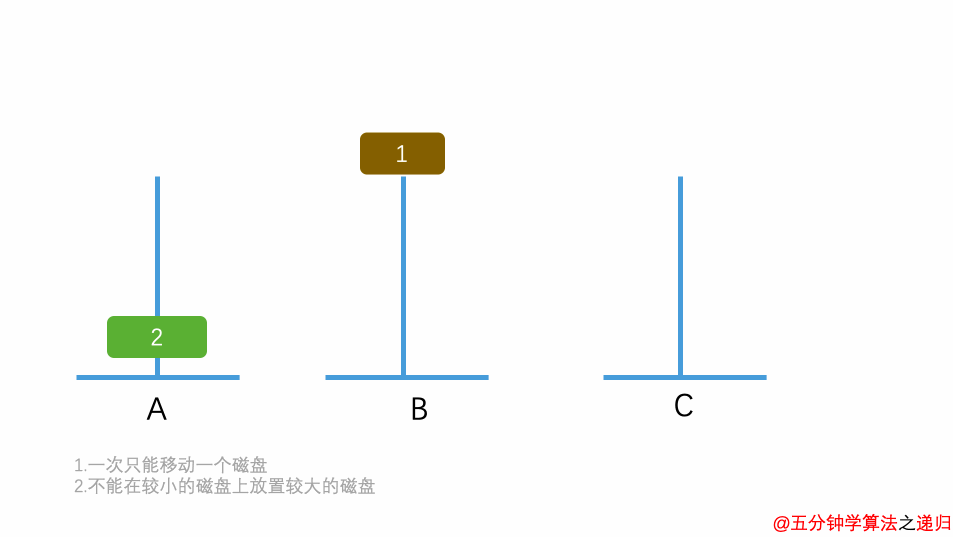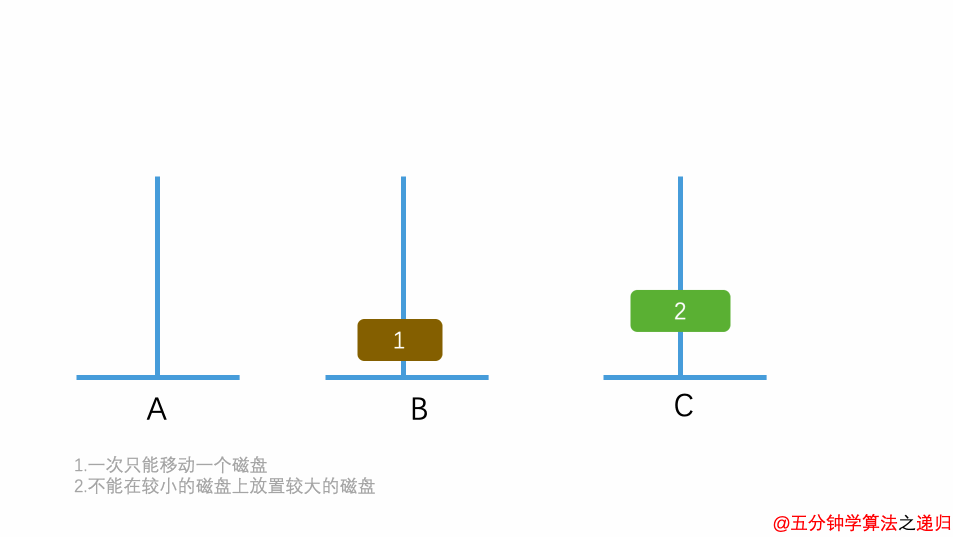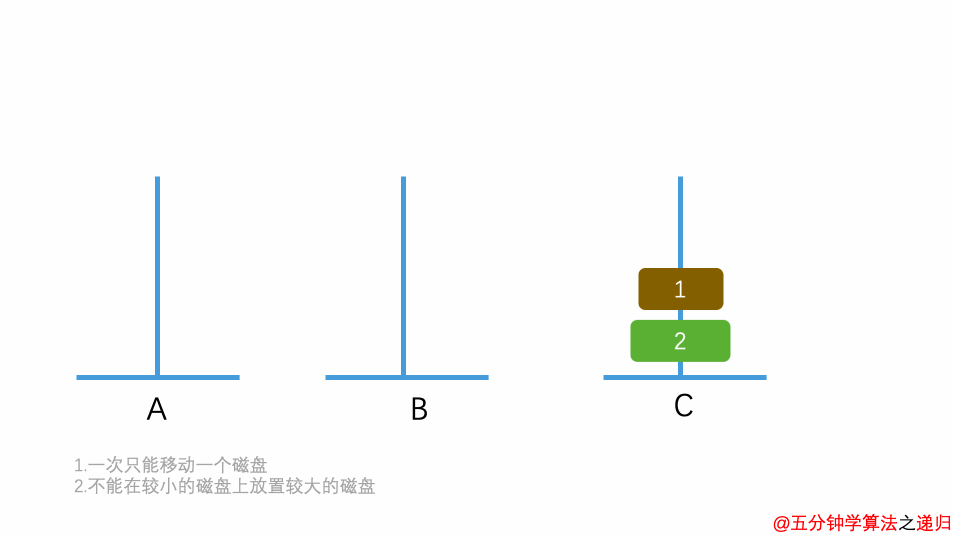
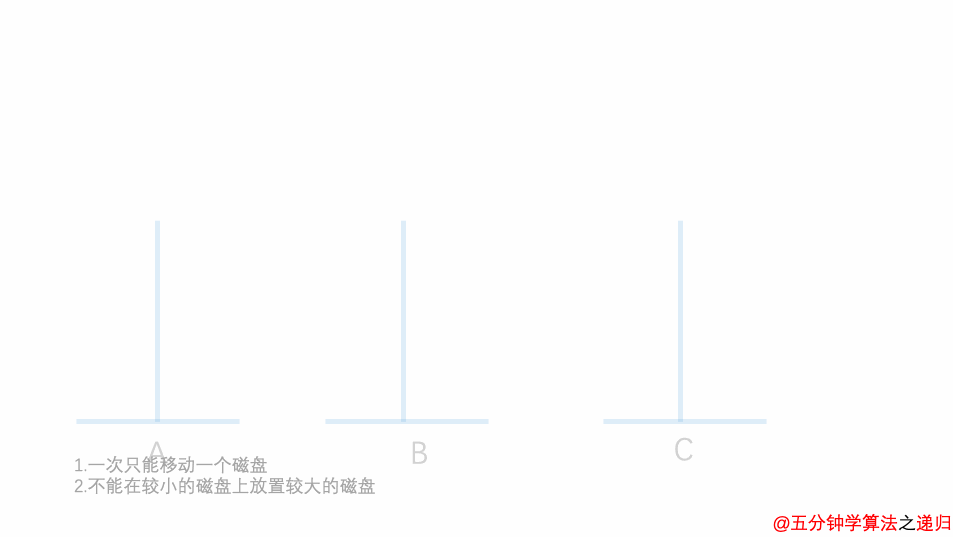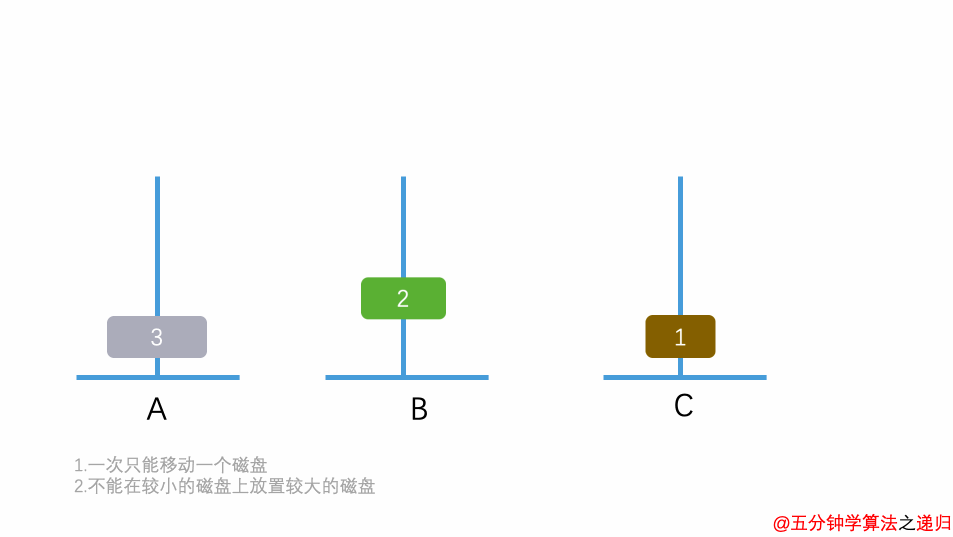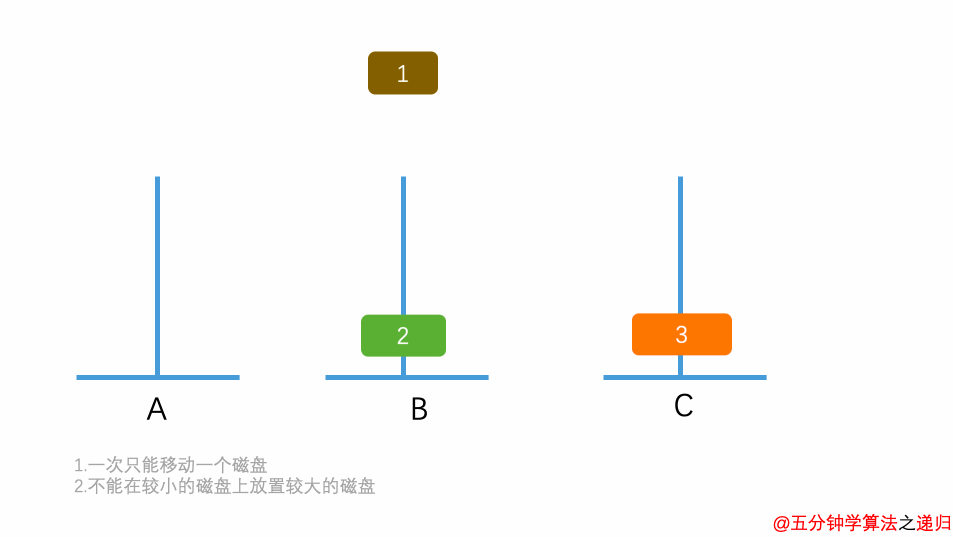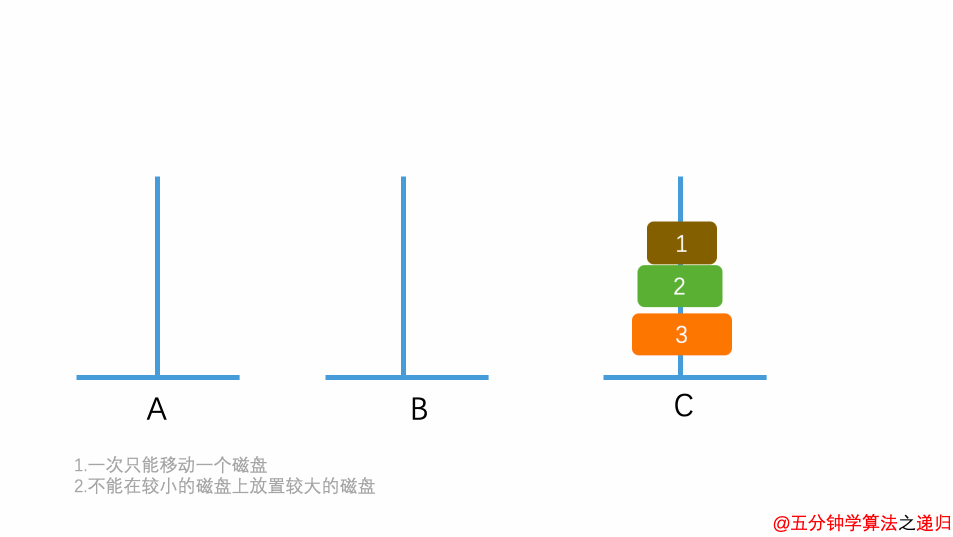
- 如果只有 1 个盘子，则不需要利用 B 塔，直接将盘子从 A 移动到 C 。
- 如果有 2 个盘子，可以先将盘子 2 上的盘子 1 移动到 B ；将盘子 2 移动到 C ；将盘子 1 移动到 C 。这说明了：可以借助 B 将 2 个盘子从 A 移动到 C ，当然，也可以借助 C 将 2 个盘子从 A 移动到 B 。
- 如果有 3 个盘子，那么根据 2 个盘子的结论，可以借助 C 将盘子 3 上的两个盘子从 A 移动到 B ；将盘子 3 从 A 移动到 C ，A 变成空座；借助 A 座，将 B 上的两个盘子移动到 C 。
- 以此类推，上述的思路可以一直扩展到 n 个盘子的情况，将将较小的 n-1个盘子看做一个整体，也就是我们要求的子问题，以借助 B 塔为例，可以借助空塔 B 将盘子A上面的 n-1 个盘子从 A 移动到 B ；将A 最大的盘子移动到 C ， A 变成空塔；借助空塔 A ，将 B 塔上的 n-2 个盘子移动到 A，将 C 最大的盘子移动到 C， B 变成空塔。。。
3 爬台阶问题
问题描述：
一个人爬楼梯，每次只能爬1个或2个台阶，假设有n个台阶，那么这个人有多少种不同的爬楼梯方法？
先从简单的开始，以 4 个台阶为例，可以通过每次爬 1 个台阶爬完楼梯：
可以通过先爬 2 个台阶，剩下的每次爬 1 个台阶爬完楼梯
在这里，可以思考一下：可以根据第一步的走法把所有走法分为两类：
- ① 第一类是第一步走了 1 个台阶
- ② 第二类是第一步走了 2 个台阶
所以 n 个台阶的走法就等于先走 1 阶后，n-1 个台阶的走法 ，然后加上先走 2 阶后，n-2 个台阶的走法。
用公式表示就是：
f(n) = f(n-1)+f(n-2)
有了递推公式，递归代码基本上就完成了一半。那么接下来考虑递归终止条件。
当有一个台阶时，我们不需要再继续递归，就只有一种走法。
所以 f(1)=1。
通过用 n = 2，n = 3 这样比较小的数试验一下后发现这个递归终止条件还不足够。
n = 2 时，f(2) = f(1) + f(0)。如果递归终止条件只有一个f(1) = 1，那 f(2) 就无法求解，递归无法结束。
所以除了 f(1) = 1 这一个递归终止条件外，还要有 f(0) = 1，表示走 0 个台阶有一种走法，从思维上以及动图上来看，这显得的有点不符合逻辑。所以为了便于理解，把 f(2) = 2 作为一种终止条件，表示走 2 个台阶，有两种走法，一步走完或者分两步来走。
总结如下：
- 假设只有一个台阶，那么只有一种走法，那就是爬 1 个台阶
- 假设有两个台阶，那么有两种走法，一步走完或者分两步来走
通过递归条件：
f(1) = 1;
f(2) = 2;
f(n) = f(n-1)+f(n-2)
很容易推导出递归代码：
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2);
}
通过上述三个示例，总结一下如何写递归代码：
- 找到如何将大问题分解为小问题的规律
- 通过规律写出递推公式
- 通过递归公式的临界点推敲出终止条件
- 将递推公式和终止条件翻译成代码
Reference
- 看动画轻松理解「递归」与「动态规划」 - https://cxyxiaowu.com/articles/2019/04/04/1554345266086.html