冒泡排序(Bubble Sort)
**冒泡排序(Bubble Sort)**是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行,直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
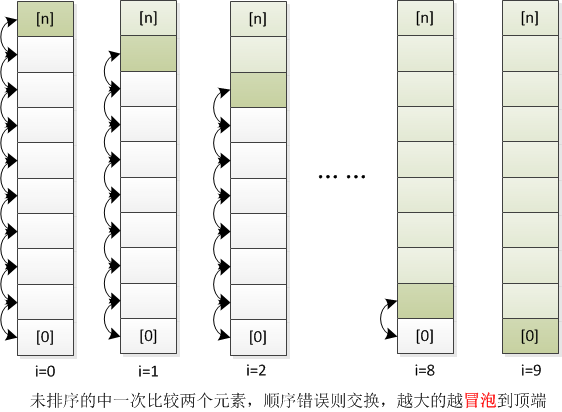
图解冒泡
第一轮冒泡
以 [ 8,2,5,9,7 ] 这组数字来做示例。
从左往右依次冒泡,将小的元素往右冒泡(移动):
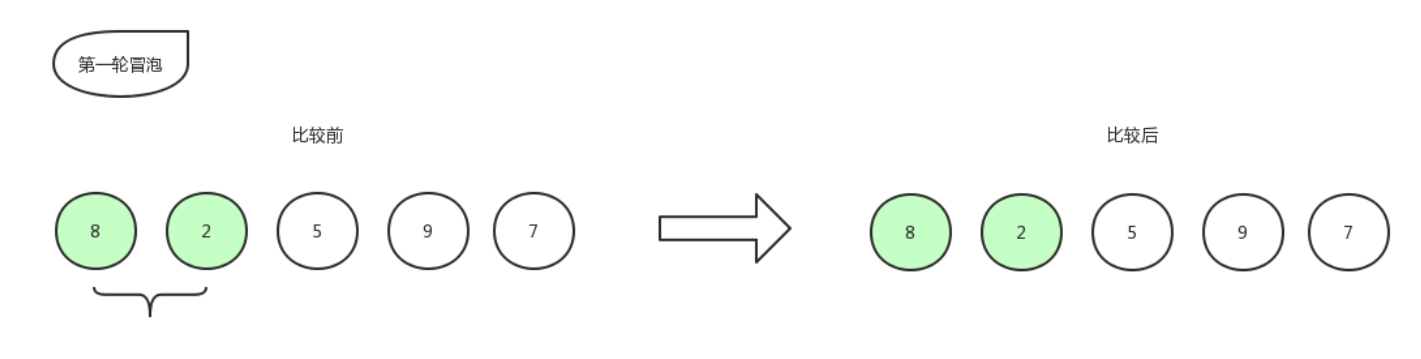
首先比较第一个数和第二个数的大小,我们发现 2 比 8 要小,那么保持原位,不做改动。位置还是 8,2,5,9,7 。
指针往右移动一格,接着比较:
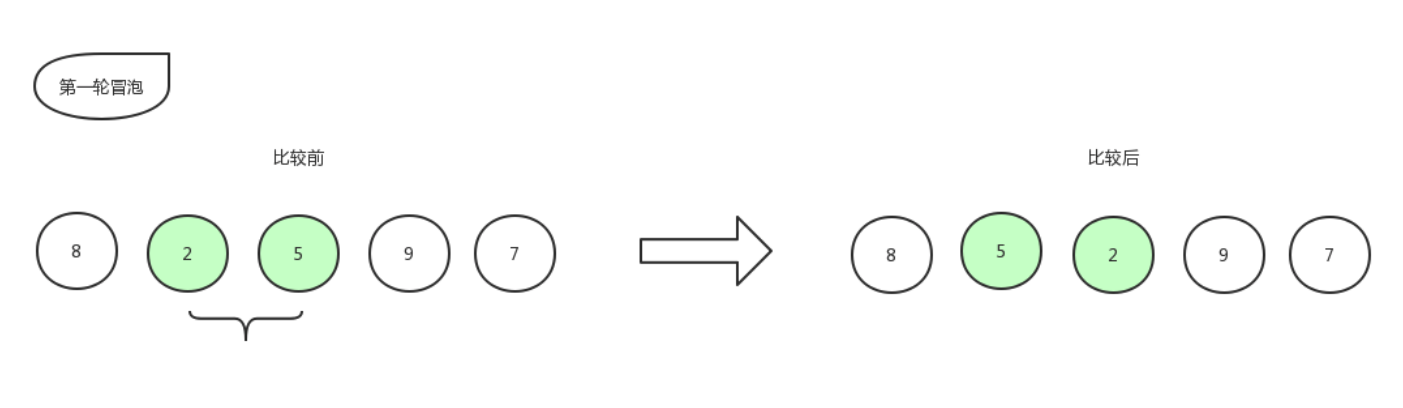
比较第二个数和第三个数的大小,发现 2 比 5 要小,所以位置交换,交换后数组更新为:[ 8,5,2,9,7 ]。
指针再往右移动一格,继续比较:
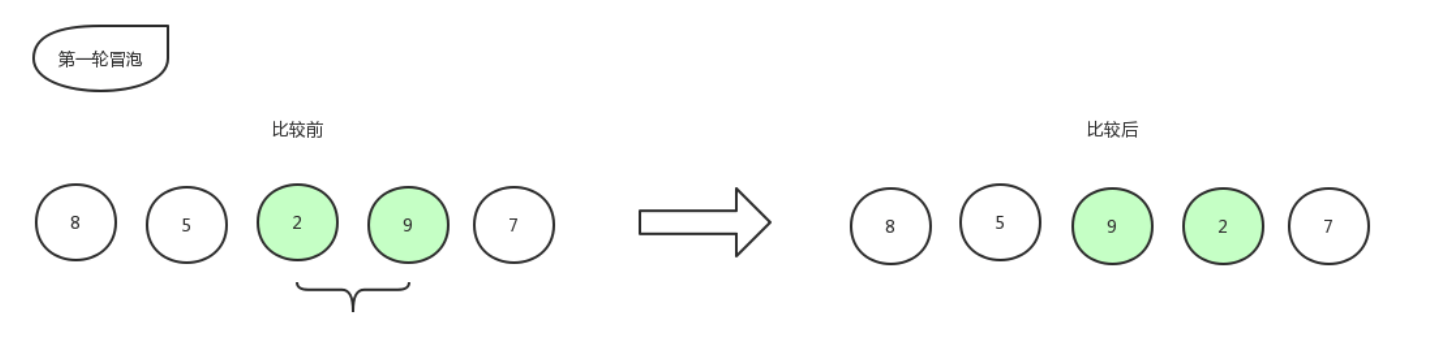
比较第三个数和第四个数的大小,发现 2 比 9 要小,所以位置交换,交换后数组更新为:[ 8,5,9,2,7 ]
同样,指针再往右移动,继续比较:
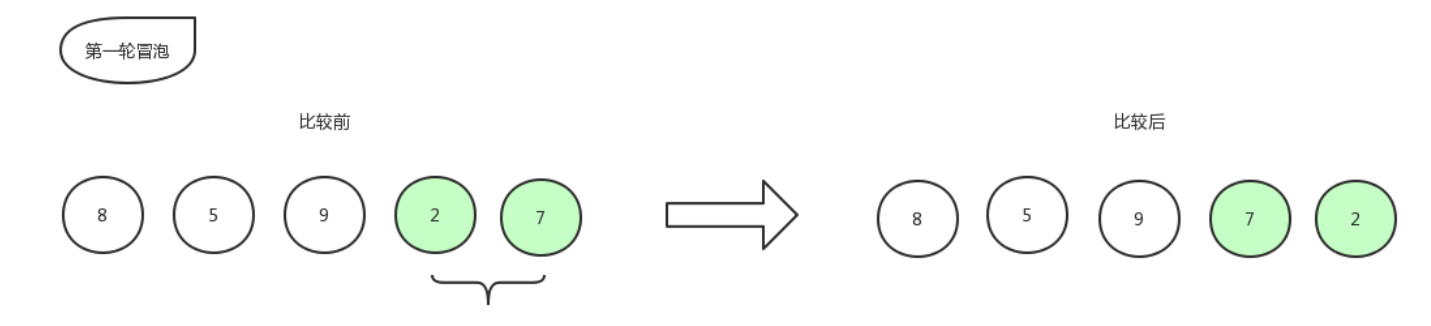
比较第 4 个数和第 5 个数的大小,发现 2 比 7 要小,所以位置交换,交换后数组更新为:[ 8,5,9,7,2 ]
下一步,指针再往右移动,发现已经到底了,则本轮冒泡结束,处于最右边的 2 就是已经排好序的数字。
通过这一轮不断的对比交换,数组中最小的数字移动到了最右边。
第二轮冒泡
接下来继续第二轮冒泡:
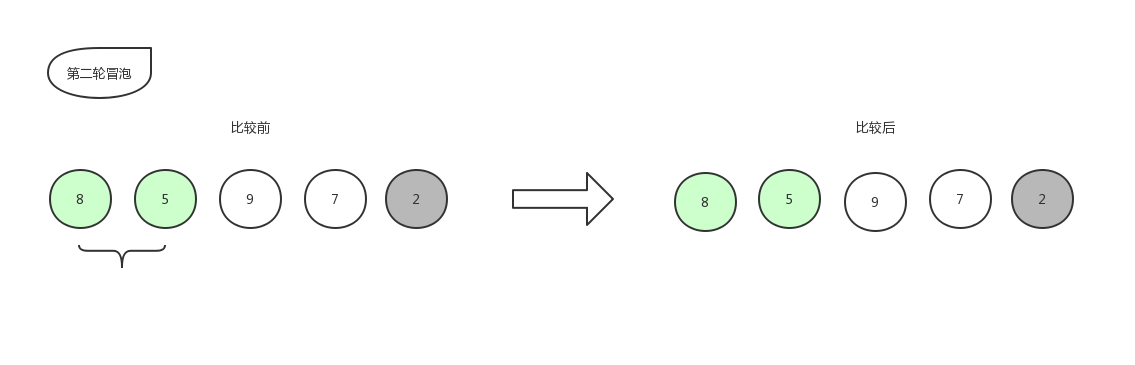
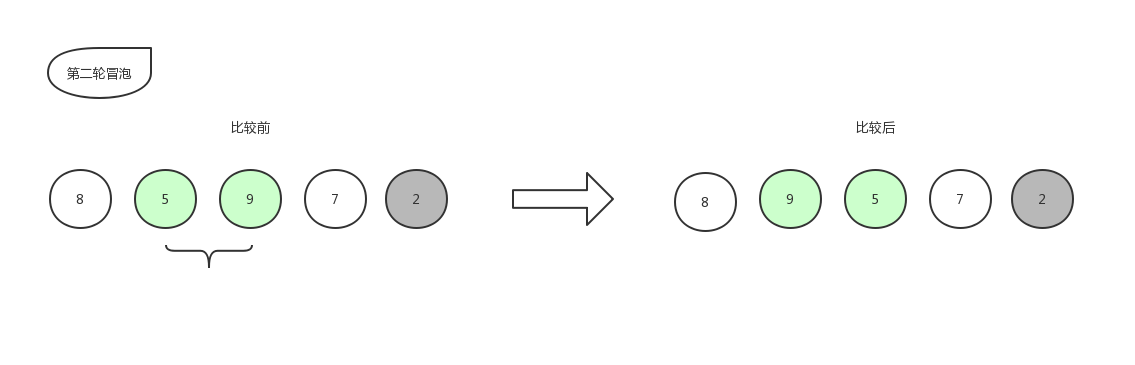
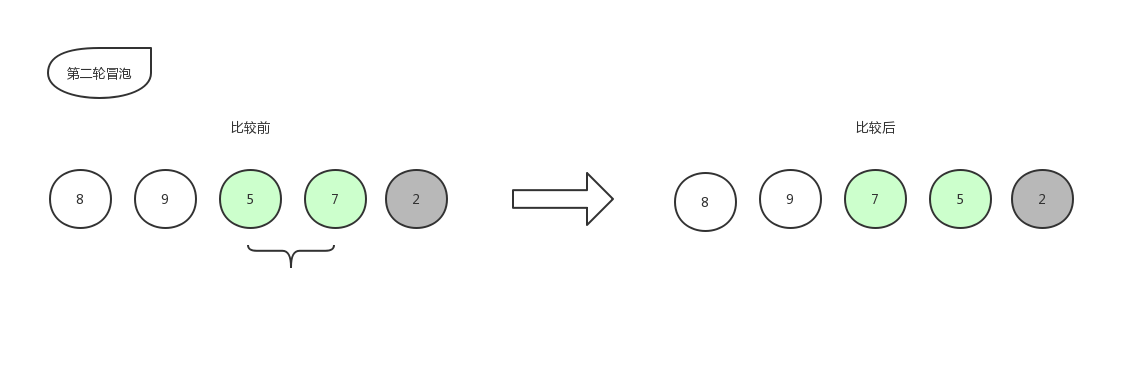
由于右边的 2 已经是排好序的数字,就不再参与比较,所以本轮冒泡结束,本轮冒泡最终冒到顶部的数字 5 也归于有序序列中,现在数组已经变化成了[ 8,9,7,5,2 ]。
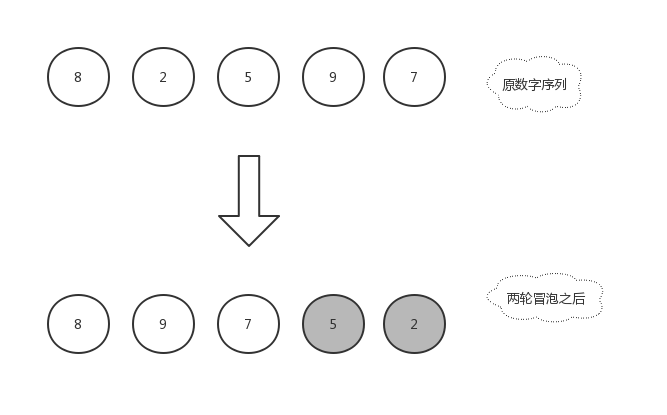
第三轮冒泡
让我们开始第三轮冒泡吧!
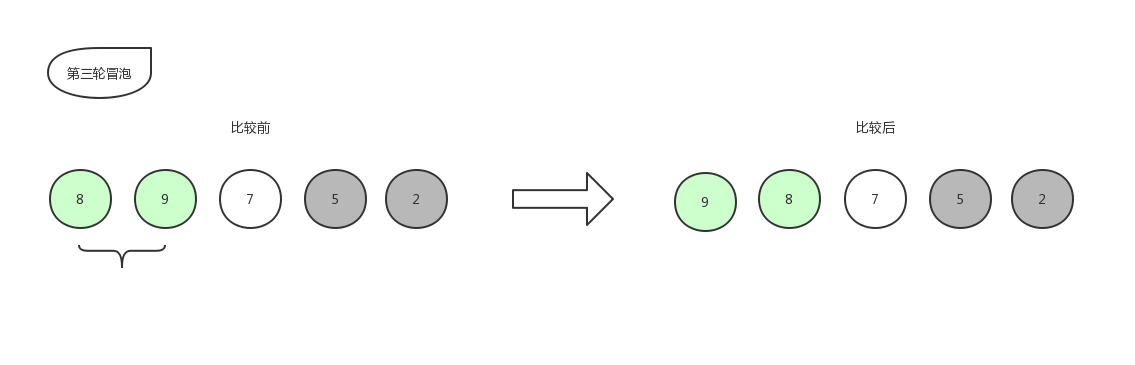
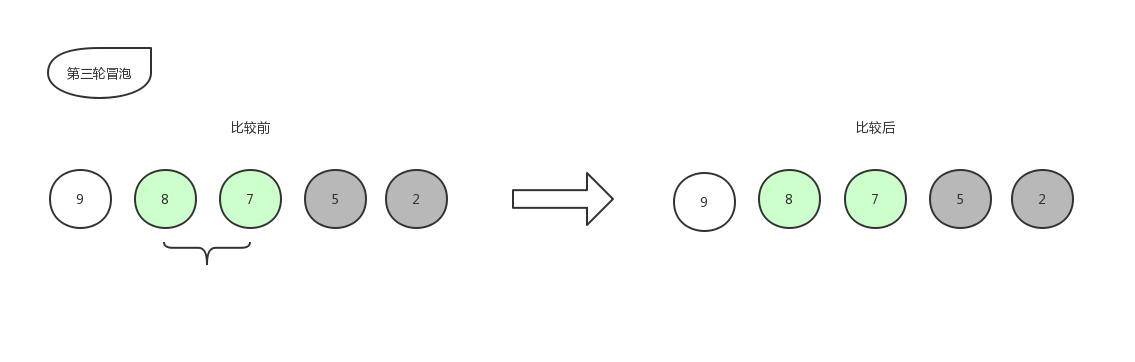
由于 8 比 7 大,所以位置不变,此时第三轮冒泡也已经结束,第三轮冒泡的最后结果是[ 9,8,7,5,2 ]
第四轮冒泡
紧接着第四轮冒泡:
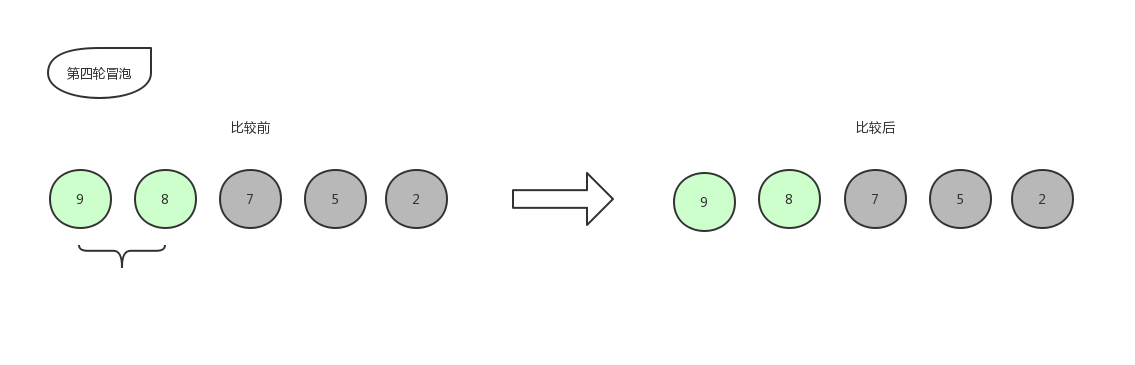
9 和 8 比,位置不变,即确定了 8 进入有序序列,那么最后只剩下一个数字 9 ,放在末尾,自此排序结束。
Solution
Java
private static int[] bubbleSort(int[] array) {
int n = arr.length;
for (int i = 0; i < n-1; i++)
for (int j = 0; j < n-i-1; j++)
if (arr[j] > arr[j+1])
{
// swap arr[j+1] and arr[i]
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
Python
def bubbleSort(arr):
n = len(arr)
# Traverse through all array elements
for i in range(n-1):
# Last i elements are already in place
for j in range(0, n-i-1):
# Traverse the array from 0 to n-i-1
# Swap if the element found is greater than the next element
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
# Example usage
arr = [64, 34, 25, 12, 22, 11, 90]
bubbleSort(arr)
print("Sorted array is:")
for i in range(len(arr)):
print("%d" % arr[i], end=" ")
复杂度分析
Bubble sort has a worst-case and average complexity of $O(n^{2})$, where n is the number of items being sorted. Most practical sorting algorithms have substantially better worst-case or average complexity, often O(nlogn). Even other $O(n^2)$ sorting algorithms, such as insertion sort, generally run faster than bubble sort, and are no more complex. For this reason, bubble sort is rarely used in practice.
| Case | Time Complexity |
|---|---|
| Best Case | O(n) |
| Average Case | O(n2) |
| Worst Case | O(n2) |
| Space Complexity | O(1) |
|---|---|
| Stable | YES |
优化
冒泡有一个最大的问题就是这种算法不管不管这个数组有序还是没序,都会将双层循环执行。
举个数组例子:一个有序的数组,[ 5,6,7,8,9 ],显然这个数组已经是有序的了,而如果将它传入冒泡排序函数中,双层循环也会从头到尾被完成执行。
而事实上,针对这个问题,我们可以设定一个临时遍历来标记该数组是否已经有序,如果有序了就不用遍历了。
public static void sort(int arr[]){
for( int i = 0;i < arr.length - 1 ; i++ ){
boolean isSort = true;
for( int j = 0;j < arr.length - 1 - i ; j++ ){
int temp = 0;
if(arr[j] < arr[j + 1]){
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
isSort = false;
}
}
if(isSort){
break;
}
}
}
Reference
- https://en.wikipedia.org/wiki/Bubble_sort
- 十大经典排序算法(动图演示)- https://www.cnblogs.com/onepixel/p/7674659.html
- https://visualgo.net/en/sorting
- 这或许是东半球讲十大排序算法最好的一篇文章 - https://cxyxiaowu.com/articles/2019/06/11/1560233679033.html