Idea
Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.

思路
- 设置固定空桶数
- 将数据放到对应的空桶中
- 将每个不为空的桶进行排序
- 拼接不为空的桶中的数据,得到结果
步骤演示
假设一组数据(长度为20)为
[63,157,189,51,101,47,141,121,157,156,194,117,98,139,67,133,181,13,28,109]
现在需要按5个分桶,进行桶排序,实现步骤如下:
- 找到数组中的最大值194和最小值13,然后根据桶数为5,计算出每个桶中的数据范围为
(194-13+1)/5=36.4; - 遍历原始数据,以第一个数据63为例,先找到该数据对应的桶序列(
Math.floor(63 - 13) / 36.4) =1),然后将该数据放入序列为1的桶中(从0开始算); - 当向同一个桶中第二次插入数据时,判断桶中已存在的数字与新插入的数字的大小,按从左到右,从小打大的顺序插入。如第一个桶已经有了63,再插入51,67后,桶中的排序为(51,63,67) ,一般通过链表来存放桶中数据。
- 全部数据装桶完毕后,按序列,从小到大合并所有非空的桶(0,1,2,3,4桶)
- 合并完之后就是排序好的数据了
步骤图示:
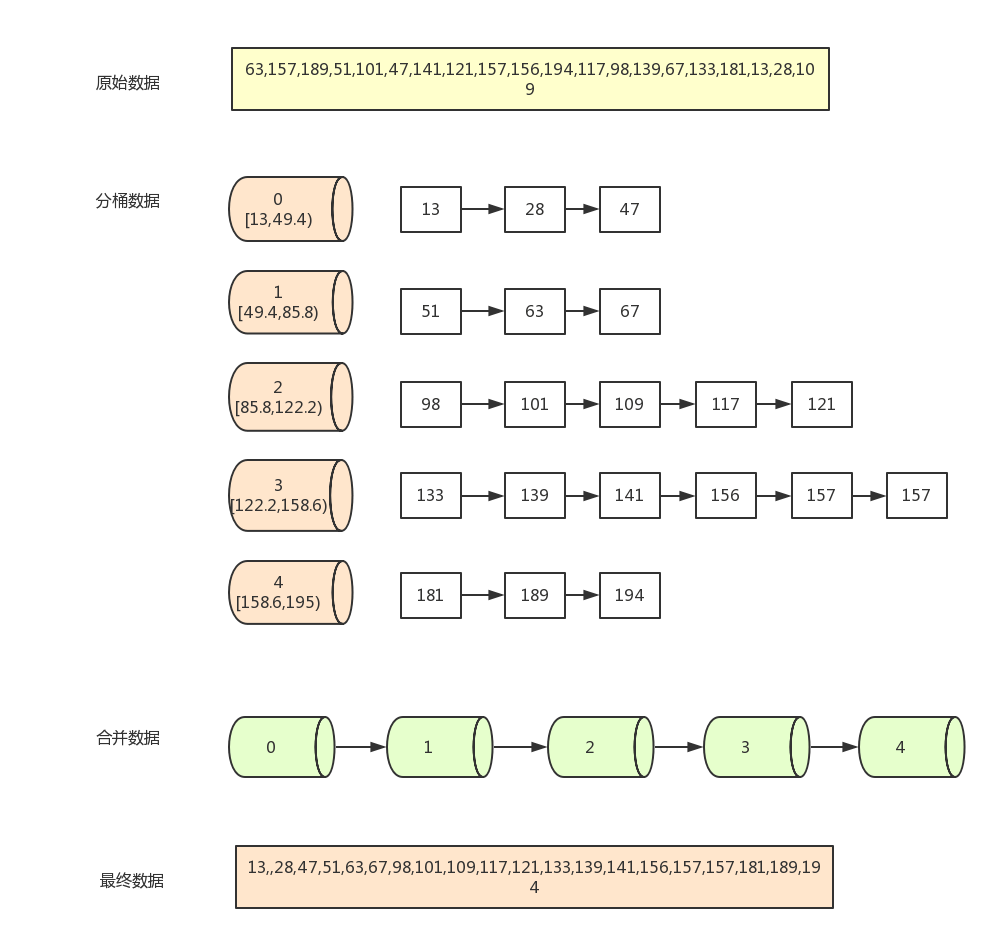
实现
Python
def bucketSort(arr):
# Find maximum value in the array and use length of the array to determine which value in the array goes into which bucket
max_value = max(arr)
size = max_value/len(arr)
# Create n empty buckets where n is equal to the length of the array
buckets_list= [[] for _ in range(len(arr))]
# Put array elements in different buckets based on size
for i in range(len(arr)):
j = int(arr[i] / size)
if j != len (arr):
buckets_list[j].append(arr[i])
else:
buckets_list[len(arr) - 1].append(arr[i])
# Sort elements within the buckets using Insertion Sort
for z in range(len(arr)):
insertionSort(buckets_list[z])
# Concatenate buckets with sorted elements into a single array
final_output = []
for x in range(len(arr)):
final_output = final_output + buckets_list[x]
return final_output
def insertionSort(b):
for i in range(1, len(b)):
up = b[i]
j = i - 1
while j >=0 and b[j] > up:
b[j + 1] = b[j]
j -= 1
b[j + 1] = up
return b
# Example usage
arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]
print("Sorted Array is")
print(bucketSort(arr))
Java
public static void main(String[] args) {
int[] intArr = {47, 85, 10, 45, 16, 34, 67, 80, 34, 4, 0, 99};
//int[] intArr = {21,11,33,70,5,25,65,55};
System.out.println("Original array- " + Arrays.toString(intArr));
bucketSort(intArr, 10);
System.out.println("Sorted array after bucket sort- " + Arrays.toString(intArr));
}
private static void bucketSort(int[] intArr, int noOfBuckets){
// Create bucket array
List<Integer>[] buckets = new List[noOfBuckets];
// Associate a list with each index
// in the bucket array
for(int i = 0; i < noOfBuckets; i++){
buckets[i] = new LinkedList<>();
}
// Assign numbers from array to the proper bucket
// by using hashing function
for(int num : intArr){
//System.out.println("hash- " + hash(num));
buckets[hash(num)].add(num);
}
// sort buckets
for(List<Integer> bucket : buckets){
Collections.sort(bucket);
}
int i = 0;
// Merge buckets to get sorted array
for(List<Integer> bucket : buckets){
for(int num : bucket){
intArr[i++] = num;
}
}
}
// A very simple hash function
private static int hash(int num){
return num/10;
}
复杂度分析
时间复杂度
Worst Case
The worst-case scenario occurs when all the elements are placed in a single bucket. The overall performance would then be dominated by the algorithm used to sort each bucket, for example $O(n^{2})$ insertion sort or $O(nlog(n))$ comparison sort algorithms, such as merge sort.
Average Case
Consider the case that the input is uniformly distributed. The first step, which is initialize the buckets and find the maximum key value in the array, can be done in O(n) time. If division and multiplication can be done in constant time, then scattering each element to its bucket also costs O(n).
桶排序最好情况下,为线性时间 O(n)。事实上,桶排序算法的总时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为 O(n)。
很显然,桶划分的越多,各个桶中的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。在额外空间充足的情况下,尽量增大桶的数量,极限情况下每个桶只有一个数据时,或者是每只桶只装一个值时,完全避开了桶内排序的操作,桶排序的最好时间复杂度就能够达到 O(n)。
比如高考总分 750 分,全国几百万人,我们只需要创建 751 个桶,循环一遍挨个扔进去,排序速度是毫秒级。
但是如果数据经过桶的划分之后,桶与桶的数据分布极不均匀,有些数据非常多,有些数据非常少,比如 [8,2,9,10,1,23,53,22,12,9000] 这十个数据,我们分成十个桶装,结果发现第一个桶装了 9 个数据,这是非常影响效率的情况,会使时间复杂度下降到 $O(nlog_2n)$,解决办法是我们每次桶内排序时判断一下数据量,如果桶里的数据量过大,那么应该在桶里面回调自身再进行一次桶排序。
空间复杂度
稳定性
稳定性是指,比如a在b前面,a=b,排序后,a仍然应该在b前面,这样就算稳定的。
桶排序中,假如升序排列,a已经在桶中,b插进来是永远都会a右边的(因为一般是从右到左,如果不小于当前元素,则插入改元素的右侧),所以桶排序是稳定的。
当然了,如果采用元素插入后再分别进行桶内排序,并且桶内排序算法采用快速排序,那么就不是稳定的。
适用范围
用排序主要适用于均匀分布的数字数组,在这种情况下能够达到最大效率。
Reference
- 排序算法之桶排序的深入理解以及性能分析 - https://dailc.github.io/2016/12/03/baseKnowlenge_algorithm_sort_bucketSort.html
- https://en.wikipedia.org/wiki/Bucket_sort