插入排序(Insertion Sort)
插入排序(Insertion-Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序的思想和我们打扑克摸牌的时候一样,从牌堆里一张一张摸起来的牌都是乱序的,我们会把摸起来的牌插入到左手中合适的位置,让左手中的牌时刻保持一个有序的状态。
那如果我们不是从牌堆里摸牌,而是左手里面初始化就是一堆乱牌呢? 一样的道理,我们把乱序的牌往手的右边挪一挪,把手的左边空出一点位置来,然后在乱牌中抽一张出来,插入到左边,再抽一张出来,插入到左边,再抽一张,插入到左边,每次插入都插入到左边合适的位置,时刻保持左边的牌是有序的,直到右边的牌抽完,则排序完毕。
图解 1
数组初始化:[ 8,2,5,9,7 ],我们把数组中的数据分成两个区域,已排序区域和未排序区域,初始化的时候所有的数据都处在未排序区域中,已排序区域是空。
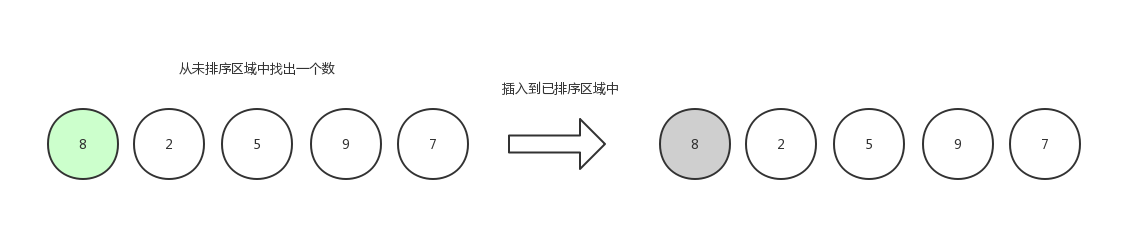
第一轮,从未排序区域中随机拿出一个数字,既然是随机,那么我们就获取第一个,然后插入到已排序区域中,已排序区域是空,那么就不做比较,默认自身已经是有序的了。(当然了,第一轮在代码中是可以省略的,从下标为1的元素开始即可)
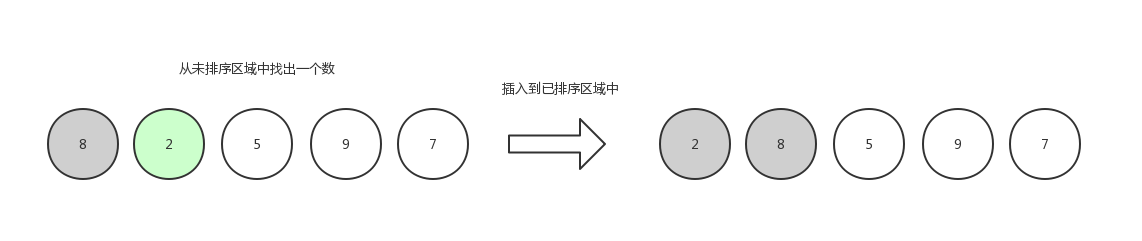
第二轮,继续从未排序区域中拿出一个数,插入到已排序区域中,这个时候要遍历已排序区域中的数字挨个做比较,比大比小取决于你是想升序排还是想倒序排,这里排升序:
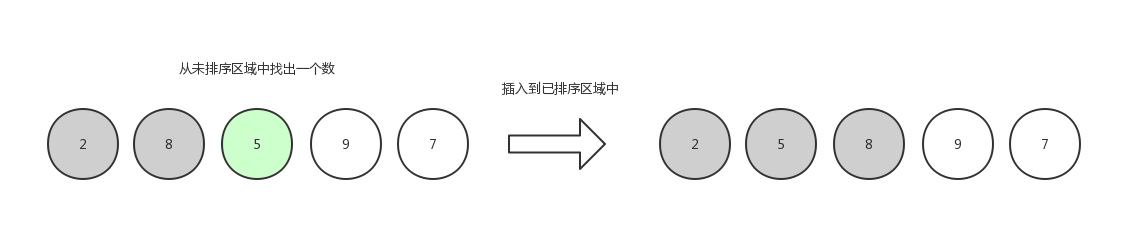
第三轮,排 5 :
第四轮,排 9 :
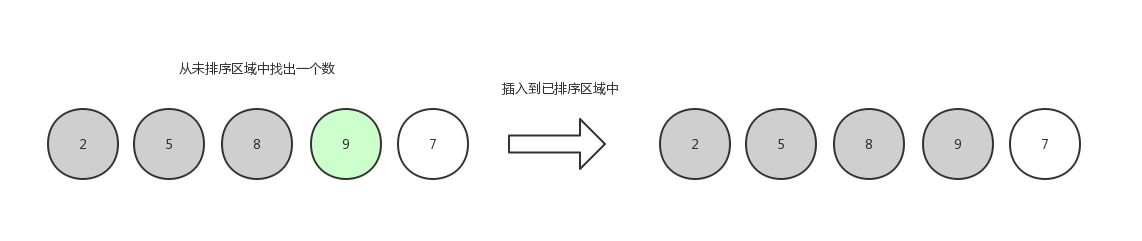
第五轮,排 7
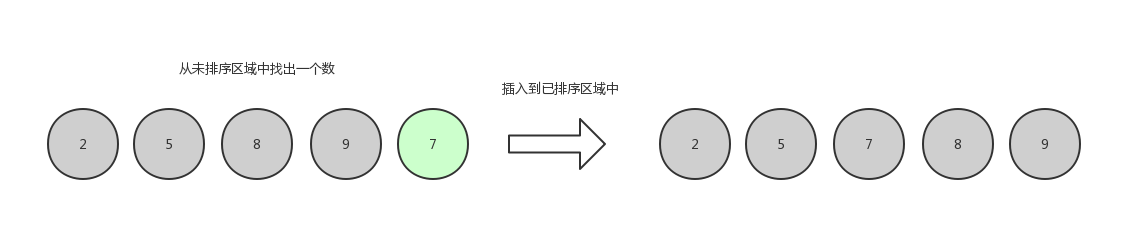
排序结束。
图解 2
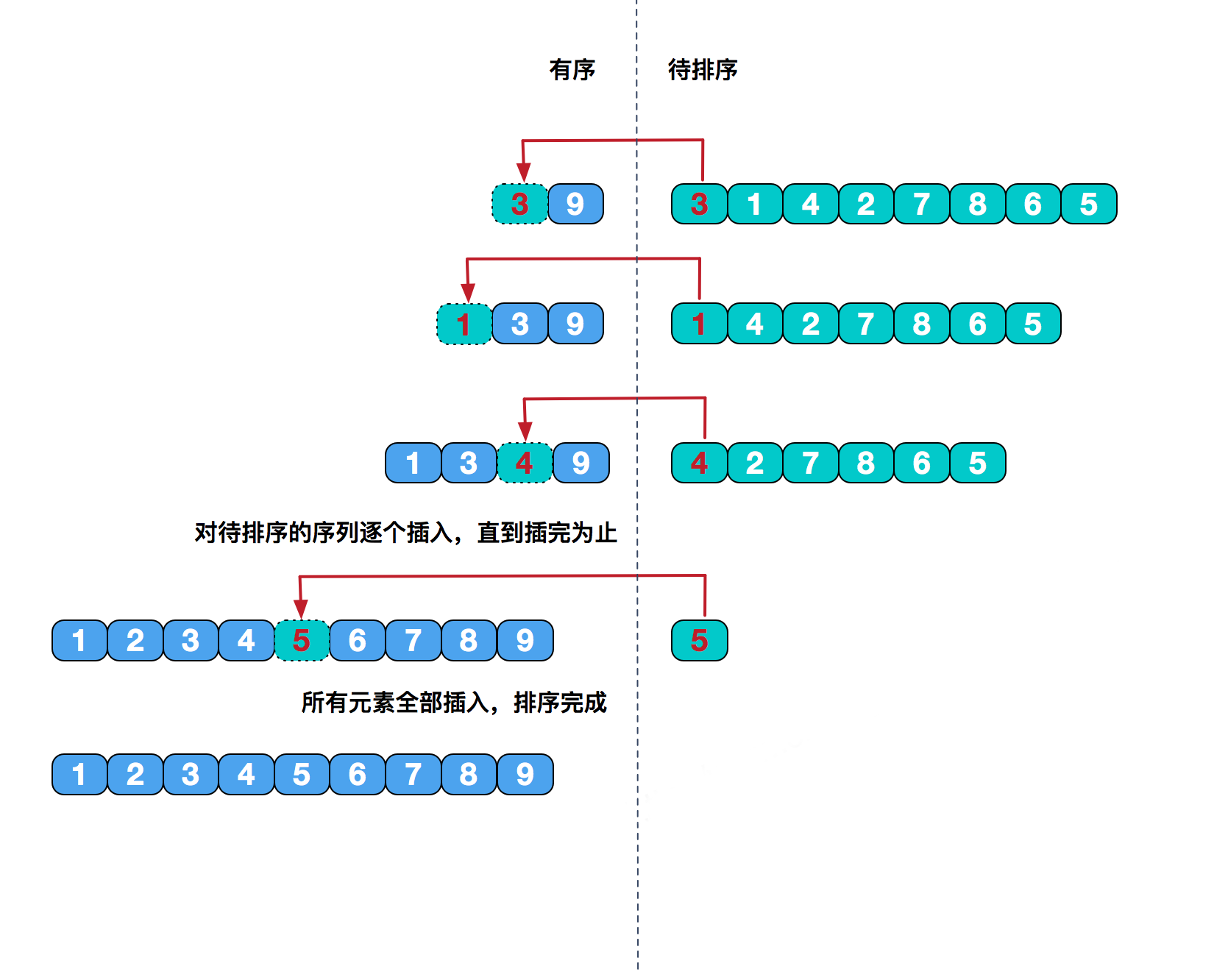
动画演示
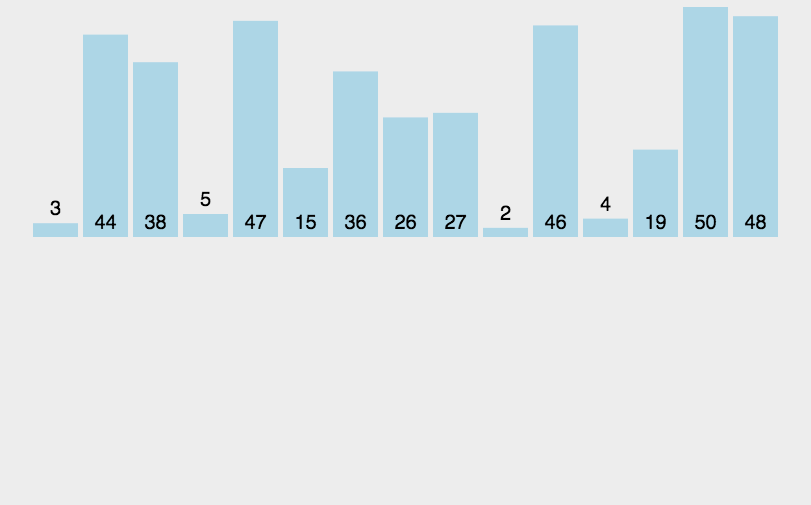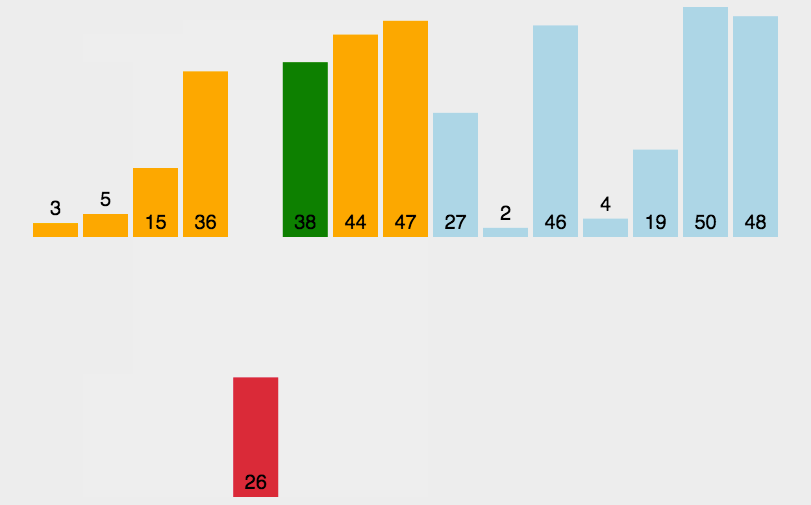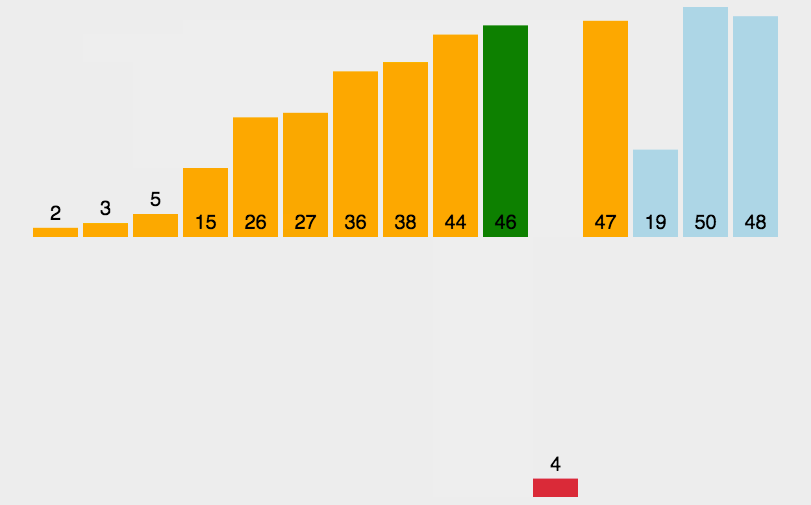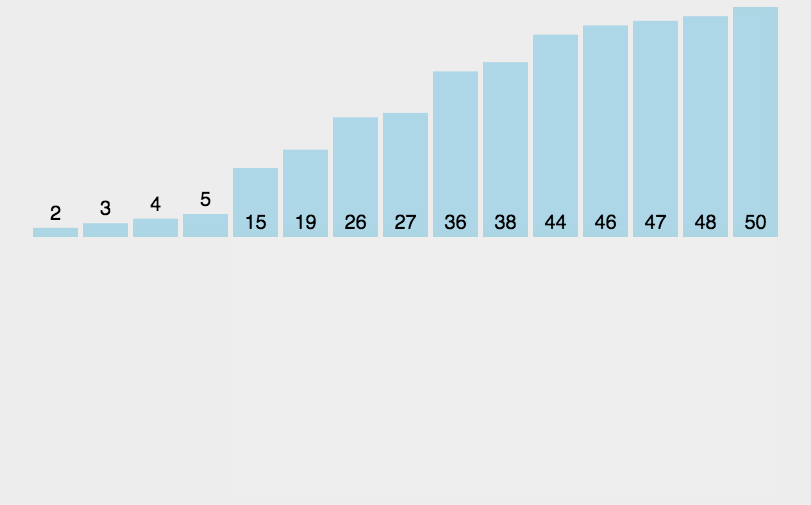
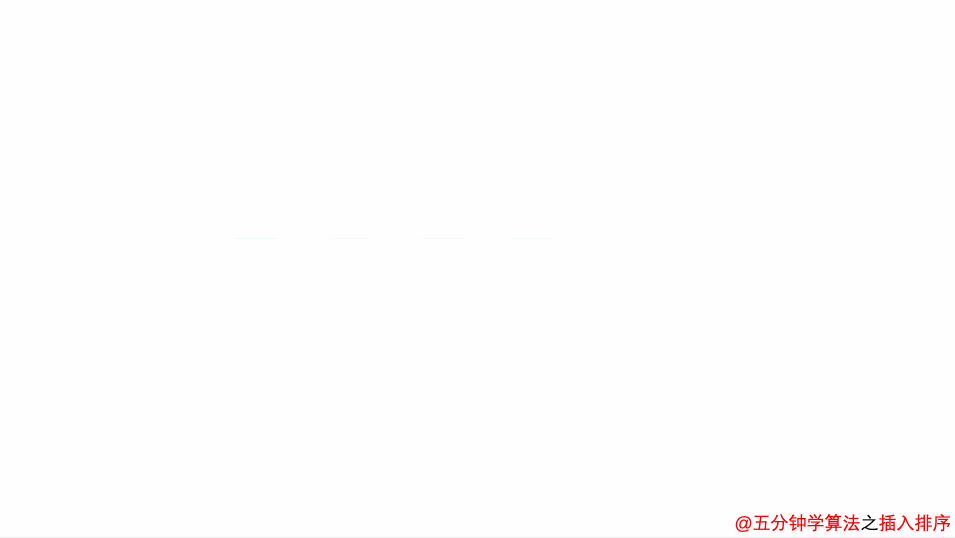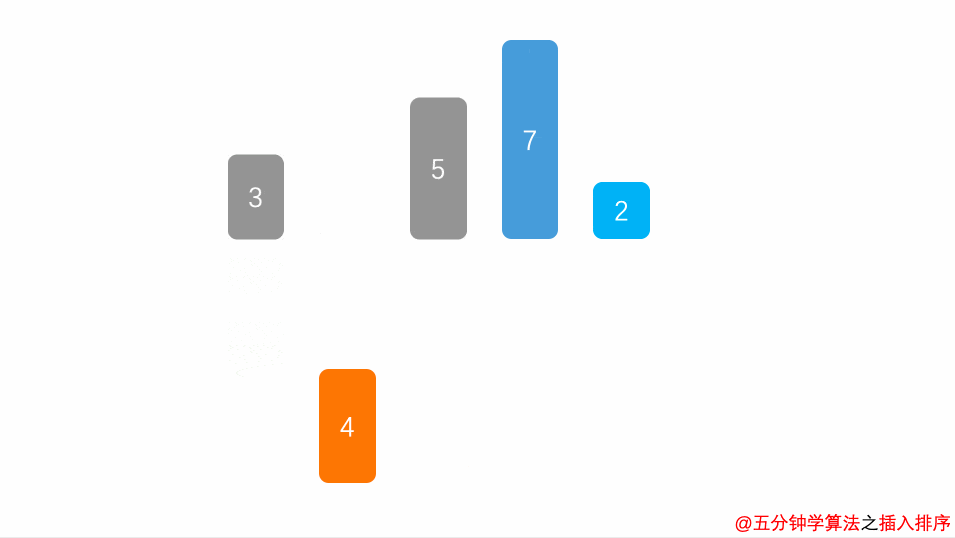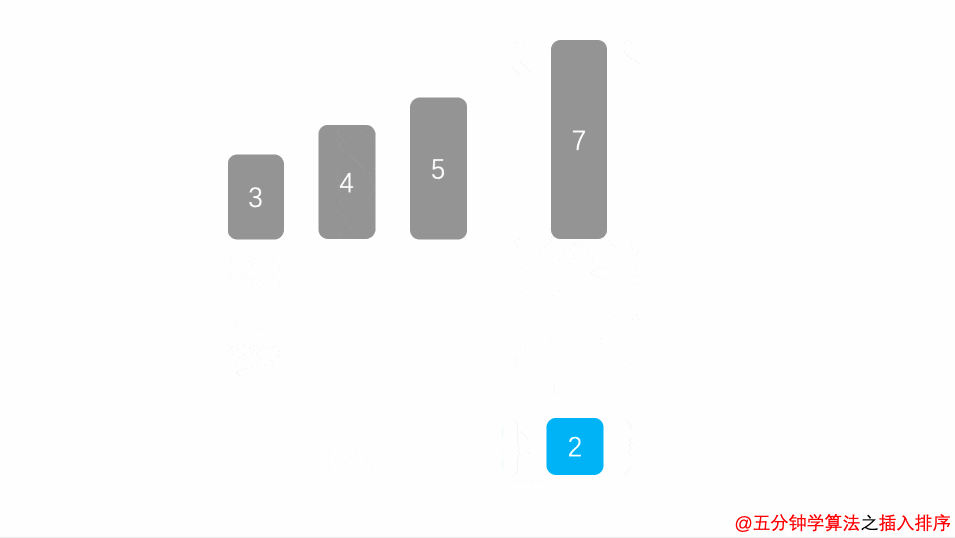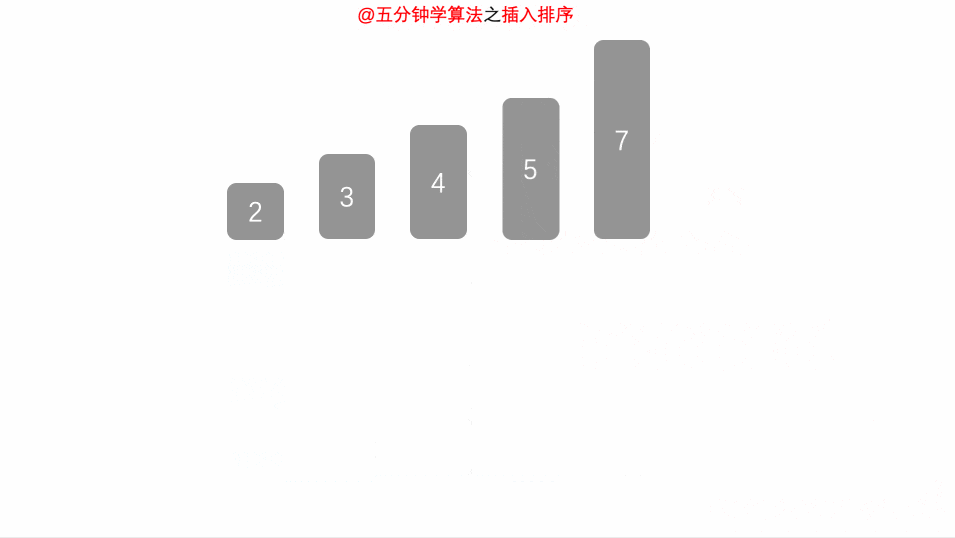
Solution
private static int[] insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; ++i) {
int value = arr[i];
int j;//插入的位置
for (j = i-1; j >= 0; j--) {
if (arr[j] > value) {
arr[j+1] = arr[j];//移动数据
} else {
break;
}
}
arr[j+1] = value; //插入数据
}
}
从代码里我们可以看出,如果找到了合适的位置,就不会再进行比较了,就好比牌堆里抽出的一张牌本身就比我手里的牌都小,那么我只需要直接放在末尾就行了,不用一个一个去移动数据腾出位置插入到中间。
所以说,最好情况的时间复杂度是 O(n),最坏情况的时间复杂度是 $O(n^2)$,然而时间复杂度这个指标看的是最坏的情况,而不是最好的情况,所以插入排序的时间复杂度是 $O(n^2)$。
性能
最好情况下的时间复杂度是 O(n),最坏情况下的时间复杂度是 $O(n^2)$,然而时间复杂度这个指标看的是最坏的情况,而不是最好的情况,所以插入排序的时间复杂度是 $O(n^2)$。
Reference
- 十大经典排序算法(动图演示)- https://www.cnblogs.com/onepixel/p/7674659.html
- https://visualgo.net/en/sorting
- GeeksforGeeks Insertion Sort - https://www.geeksforgeeks.org/insertion-sort/
- 这或许是东半球讲十大排序算法最好的一篇文章 - https://cxyxiaowu.com/articles/2019/06/11/1560233679033.html
- 图解排序算法(一)之3种简单排序(选择,冒泡,直接插入) - https://www.cnblogs.com/chengxiao/p/6103002.html