归并排序(Merge Sort)
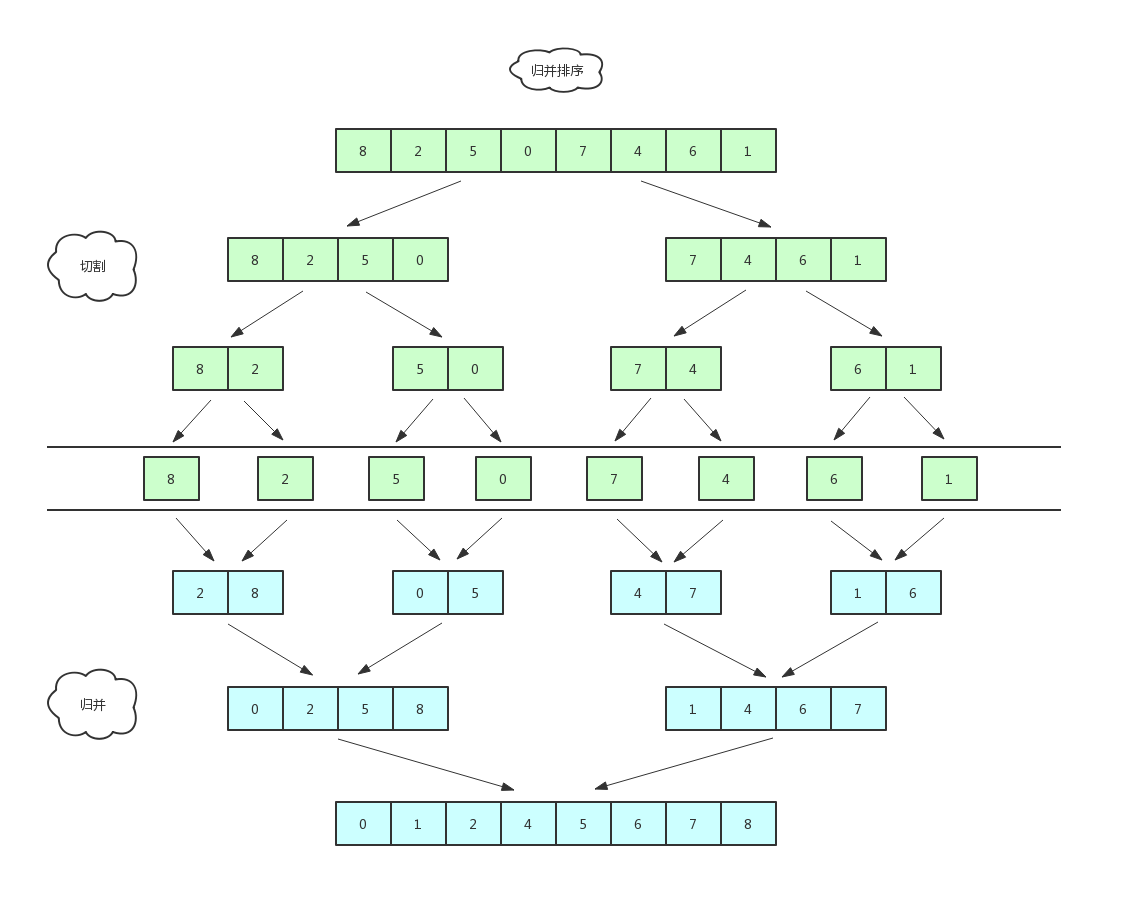
归并字面上的意思是合并,归并算法的核心思想是分治法(divide-and-conquer method),就是将一个数组一刀切两半,递归切,直到切成单个元素,然后重新组装合并,单个元素合并成小数组,两个小数组合并成大数组,直到最终合并完成,排序完毕。

图解归并排序
我们以[ 8,2,5,9,7 ]这组数字来举例
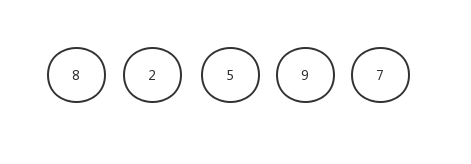
首先,一刀切两半:
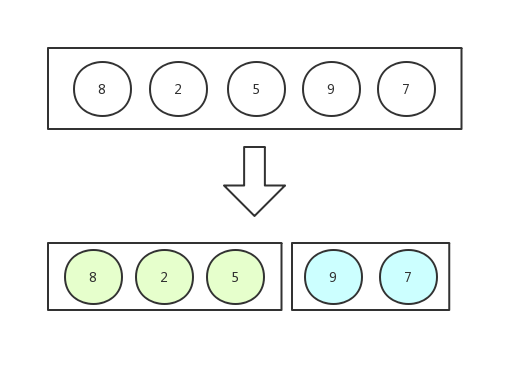
再切:
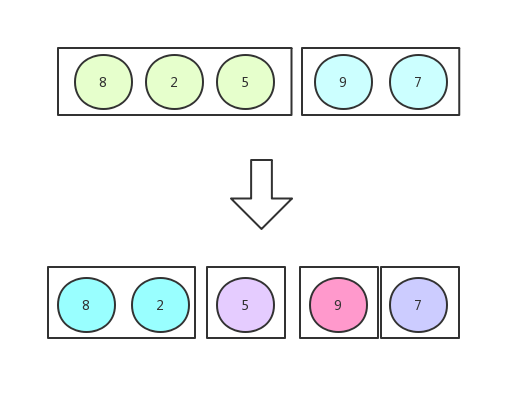
再切

粒度切到最小的时候,就开始归并
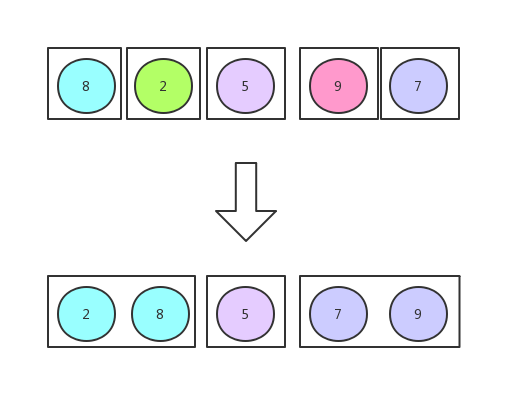


数据量设定的比较少,是为了方便图解,数据量为单数,是为了让你看到细节,下面我画了一张更直观的图可能你会更喜欢:
分析
分而治之
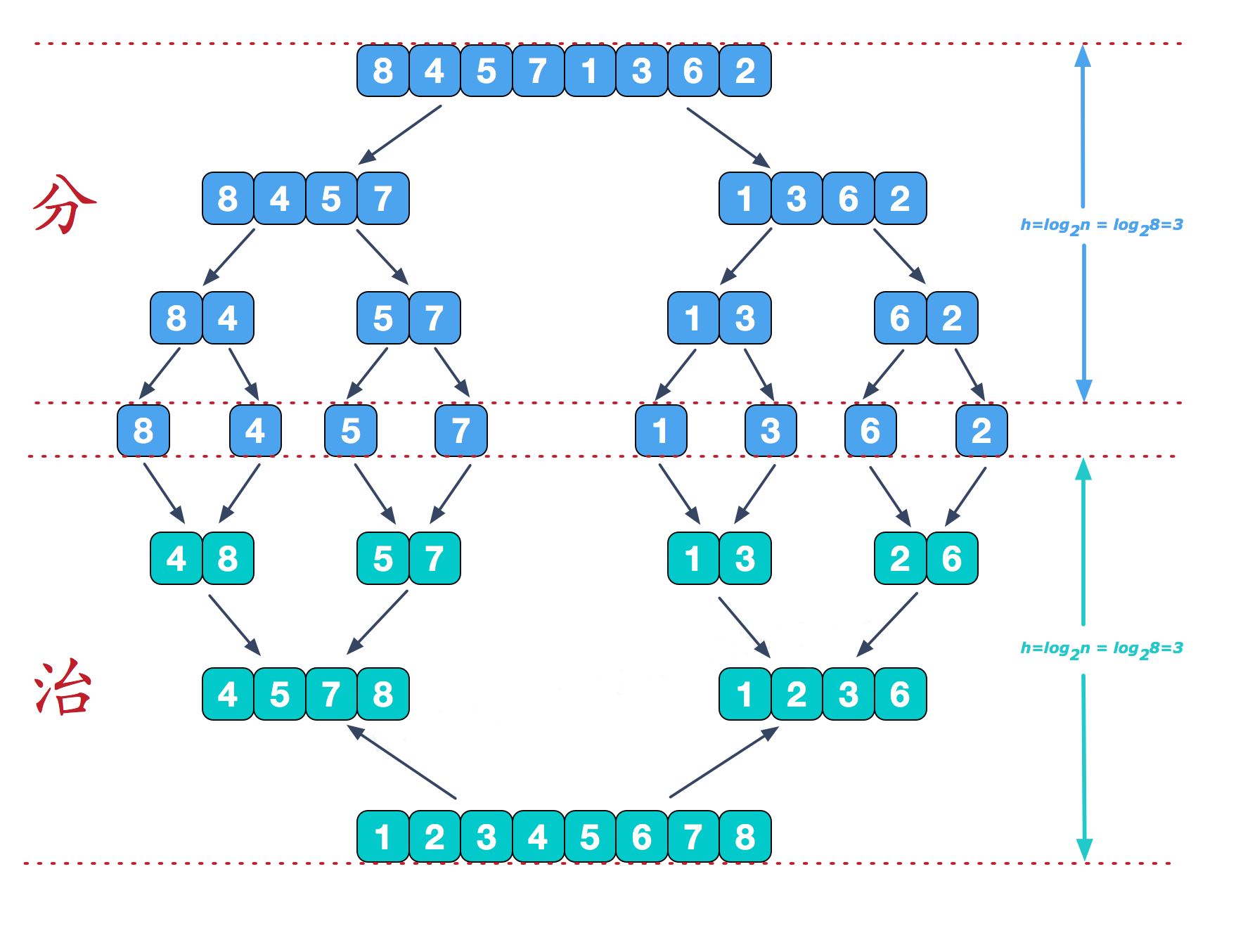
合并相邻有序子序列
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。


代码实现
我们上面讲过,归并排序的核心思想是分治,分而治之,将一个大问题分解成无数的小问题进行处理,处理之后再合并,这里我们采用递归来实现:
public void sortIntegers2(int[] A) {
// use a shared temp array, the extra memory is O(n) at least
int[] temp = new int[A.length];
mergeSort(A, 0, A.length - 1, temp);
}
private void mergeSort(int[] A, int start, int end, int[] temp) {
if (start >= end) {
return;
}
int left = start, right = end;
int mid = (start + end) / 2;
mergeSort(A, start, mid, temp);
mergeSort(A, mid+1, end, temp);
merge(A, start, mid, end, temp);
}
private void merge(int[] A, int start, int mid, int end, int[] temp) {
int left = start;
int right = mid+1;
int index = start;
// merge two sorted subarrays in A to temp array
while (left <= mid && right <= end) {
if (A[left] < A[right]) {
temp[index++] = A[left++];
} else {
temp[index++] = A[right++];
}
}
while (left <= mid) {
temp[index++] = A[left++];
}
while (right <= end) {
temp[index++] = A[right++];
}
// copy temp back to A
for (index = start; index <= end; index++) {
A[index] = temp[index];
}
}
我们可以发现 merge 方法中只有一个 for 循环,直接就可以得出每次合并的时间复杂度为 O(n) ,而分解数组每次对半切割,属于对数时间 O(log n) ,合起来等于 O(log2n) ,也就是说,总的时间复杂度为 O(nlogn) 。
关于空间复杂度,其实大部分人写的归并都是在 merge 方法里面申请临时数组,用临时数组来辅助排序工作,空间复杂度为 O(n),而我这里做的是原地归并,只在最开始申请了一个临时数组,所以空间复杂度为 O(1)。
Complexity
- Worst-Case Complexity: O(n log n)
- Best-Case Complexity: O(n log n)
- Average-Case Complexity: O(n log n)
- Space Complexity: O(n)
Reference
- 这或许是东半球讲十大排序算法最好的一篇文章 - https://cxyxiaowu.com/articles/2019/06/11/1560233679033.html
- 图解排序算法(四)之归并排序 - https://www.cnblogs.com/chengxiao/p/6194356.html