快速排序(Quick Sort)
快速排序的核心思想也是分治法(Divide and Conquer Method),分而治之。
它的实现方式是每次从序列中选出一个基准值(pivot),其他数依次和基准值做比较,比基准值大的放右边,比基准值小的放左边,然后再对左边和右边的两组数分别选出一个基准值,进行同样的比较移动,重复步骤,直到最后都变成单个元素,整个数组就成了有序的序列。
单边扫描
Solution
/* This function takes last element as pivot,
places the pivot element at its correct
position in sorted array, and places all
smaller (smaller than pivot) to left of
pivot and all greater elements to right
of pivot */
int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low-1); // index of smaller element
for (int j=low; j<high; j++)
{
// If current element is smaller than or
// equal to pivot
if (arr[j] <= pivot)
{
i++;
// swap arr[i] and arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// swap arr[i+1] and arr[high] (or pivot)
int temp = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp;
return i+1;
}
/* The main function that implements QuickSort()
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void sort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is
now at right place */
int pi = partition(arr, low, high);
// Recursively sort elements before
// partition and after partition
sort(arr, low, pi-1);
sort(arr, pi+1, high);
}
}
双边扫描
Solution
public class Solution {
public Random rand;
public void sortIntegers2(int[] A) {
rand = new Random();
// write your code here
quickSort(A, 0, A.length - 1);
}
public void quickSort(int[] A, int start, int end) {
if (start >= end) {
return;
}
// 注意,这里再选择 pivot 时,采用了生成一个随机数的方法,这样做的结果是使快排算法的时间复杂度无限趋近于 nlogn,
int index = rand.nextInt(end - start + 1) + start;
int pivot = A[index];
int left = start;
int right = end;
while (left <= right) {
while (left <= right && A[left] < pivot) {
left ++;
}
while (left <= right && A[right] > pivot) {
right --;
}
if (left <= right) {
int temp = A[left];
A[left] = A[right];
A[right] = temp;
left ++;
right --;
}
}
// A[start... right]
quickSort(A, start, right);
// A[left ... end]
quickSort(A, left, end);
}
}
解析
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个 10 个数进行排序。首先在这个序列中随便找一个数作为基准数。
不要被这个名词吓到了,就是找一个用来参照的数,待会你就知道它用来做啥的了。
为了方便,就让第一个数 6 作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在 6 的右边,比基准数小的数放在 6 的左边,类似下面这种排列。
3 1 2 5 4 6 9 7 10 8
在初始状态下,数字 6 在序列的第 1 位。我们的目标是将 6 挪到序列中间的某个位置,假设这个位置是 k。现在就需要寻找这个 k,并且以第 k 位为分界点,左边的数都小于等于 6,右边的数都大于等于 6。想一想,你有办法可以做到这点吗?
方法其实很简单:分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于 6 的数,再从左往右找一个大于 6 的数,然后交换他们。这里可以用两个变量 i 和 j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵 i”和“哨兵 j”。刚开始的时候让哨兵 i 指向序列的最左边(即 i=1),指向数字 6。让哨兵 j 指向序列的最右边(即 j=10),指向数字 8。
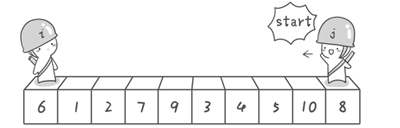
首先哨兵 j 开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵 j 先出动,这一点非常重要。哨兵 j 一步一步地向左挪动(即 j–),直到找到一个小于 6 的数停下来。接下来哨兵 i 再一步一步向右挪动(即 i++),直到找到一个数大于 6 的数停下来。最后哨兵 j 停在了数字 5 面前,哨兵 i 停在了数字 7 面前。
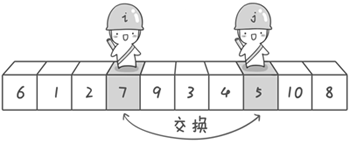
现在交换哨兵 i 和哨兵 j 所指向的元素的值。交换之后的序列如下:
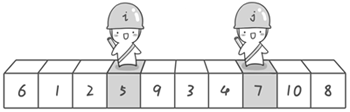
到此,第一次交换结束。接下来开始哨兵 j 继续向左挪动(再友情提醒,每次必须是哨兵 j 先出发)。他发现了 4(比基准数 6 要小,满足要求)之后停了下来。哨兵 i 也继续向右挪动的,他发现了 9(比基准数 6 要大,满足要求)之后停了下来。
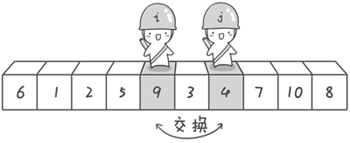
此时再次进行交换,交换之后的序列如下:
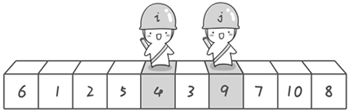
第二次交换结束,“探测”继续。哨兵 j 继续向左挪动,他发现了 3(比基准数 6 要小,满足要求)之后又停了下来。哨兵 i 继续向右移动,糟啦!此时哨兵 i 和哨兵 j 相遇了,哨兵 i 和哨兵 j 都走到 3 这里了。说明此时“探测”结束。
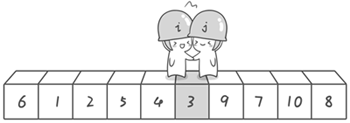
我们将基准数 6 和 3 进行交换:
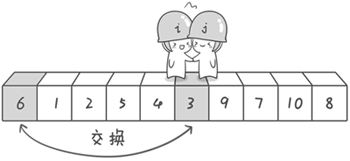
交换之后的序列如下:
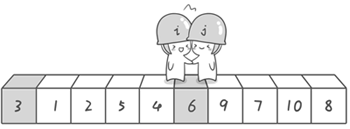
到此第一轮“探测”真正结束。此时以基准数 6 为分界点,6 左边的数都小于等于 6,6 右边的数都大于等于 6。回顾一下刚才的过程,其实哨兵 j 的使命就是要找小于基准数的数,而哨兵 i 的使命就是要找大于基准数的数,直到 i 和 j 碰头为止。
OK,解释完毕。现在基准数 6 已经归位,它正好处在序列的第 6 位。此时我们已经将原来的序列,以 6 为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“ 9 7 10 8 ”。
接下来还需要分别处理这两个序列。因为 6 左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理 6 左边和右边的序列即可。现在先来处理 6 左边的序列现吧。
左边的序列是“3 1 2 5 4”。请将这个序列以 3 为基准数进行调整,使得 3 左边的数都小于等于 3,3 右边的数都大于等于 3。好了开始动笔吧。
如果你模拟的没有错,调整完毕之后的序列的顺序应该是。
2 1 3 5 4
OK,现在 3 已经归位。接下来需要处理 3 左边的序列“ 2 1 ”和右边的序列“5 4”。
对序列“ 2 1 ”以 2 为基准数进行调整,处理完毕之后的序列为“1 2”,到此 2 已经归位。序列“1”只有一个数,也不需要进行任何处理。至此我们对序列“ 2 1 ”已全部处理完毕,得到序列是“1 2”。序列“5 4”的处理也仿照此方法,最后得到的序列如下。
1 2 3 4 5 6 9 7 10 8
对于序列“9 7 10 8”也模拟刚才的过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列,如下。
1 2 3 4 5 6 7 8 9 10
到此,排序完全结束。细心的同学可能已经发现,快速排序的每一轮处理其实就是将这一轮的基准数归位,直到所有的数都归位为止,排序就结束了。
性能分析
快速排序的时间复杂度和归并排序一样,$O(n log_2 n)$,但这是建立在每次切分都能把数组一刀切两边所包含的元素个数差不多大的前提下。
而如果每次切分都切出了“左边部分不包含所有元素,而右边部分包含所有元素”,则此时在这个场景下快速排序的时间复杂度就从 $O(n log_2 n)$ 退化到了 $O(n^2)$。换句话说,快速排序的平均时间复杂度为$O(n log_2 n)$,而其最坏时间复杂度为 $O(n^2)$。
举个例子,比如排一个有序的序列,如[ 9,8,7,6,5,4,3,2,1 ],如果在每次选取基准值(pivot)时, 都选择最左边的元素,那么在每次进行 partion 的过程,右指针都需要移动 n-1次(一直移动,直到指向最左边的元素)。在这种情况下,快速排序的时间复杂度就退化成了 $O(n^2)$。
显然,用什么方法来选取基准值,会影响对于特定数组使用快速排序的时间复杂度。
理论上来说,应该做到随机选取 pivot, 才能保证$O(n log_2 n)$ 的平均时间复杂度。
另外,快速排序的空间复杂度为 O(1)。
Reference
- 【图解数据结构】一组动画彻底理解快速排序 - https://mp.weixin.qq.com/s?__biz=MzUyNjQxNjYyMg==&mid=2247483963&idx=1&sn=dd58fafb86a43eec3dcdc2a2def8fcb7&chksm=fa0e6dbacd79e4ac5dbf7f507264d2b5a4ecc9e78babbce9917b2e08ac05f5434c697839f46a&scene=21#wechat_redirect
- https://www.geeksforgeeks.org/quick-sort/
- 算法 3:最常用的排序——快速排序 - https://wiki.jikexueyuan.com/project/easy-learn-algorithm/fast-sort.html