选择排序(Selection Sort)
选择排序的思路是这样的:首先,找到数组中最小的那个元素,其次,将它和数组的第 一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。再次,在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此往复,直到将整个数组排序。
这种方法叫做选择排序(Selection Sort),因为它在不断地选择剩余元素之中的最小者。
如下所示,选择排序的内循环只是在比较当前元素与目前已知的最小元素(以及将当前索引加 1 和检查是否代码越界),这已经简单到了极点。交换元素的代码写在内循环之外,每次交换都能排定一个元素,因此交换的总次数是 N 。所以算法的时间效率取决于比较的次数。
特点
总的来说,选择排序是一种很容易理解和实现的简单排序算法,它有两个很鲜明的特点。 运行时间和输入无关。为了找出最小的元素而扫描一遍数组并不能为下一遍扫描提供什么信息。 这种性质在某些情况下是缺点,因为使用选择排序的人可能会惊讶地发现,一个已经有序的数组或是主键全部相等的数组和一个元素随机排列的数组所用的排序时间竟然一样长!我们将会看到,其他算法会更善于利用输入的初始状态。
数据移动是最少的。每次交换都会改变两个数组元素的值,因此选择排序用了 N 次交换——交换次数和数组的大小是线性关系。我们将研究的其他任何算法都不具备这个特征(大部分的增长数量级都是线性对数或是平方级别)。
图解
我们还是以[ 8,2,5,9,7 ]这组数字做例子。
第一次选择,先找到数组中最小的数字 2 ,然后和第一个数字交换位置。(如果第一个数字就是最小值,那么自己和自己交换位置,也可以不做处理,就是一个 if 的事情)
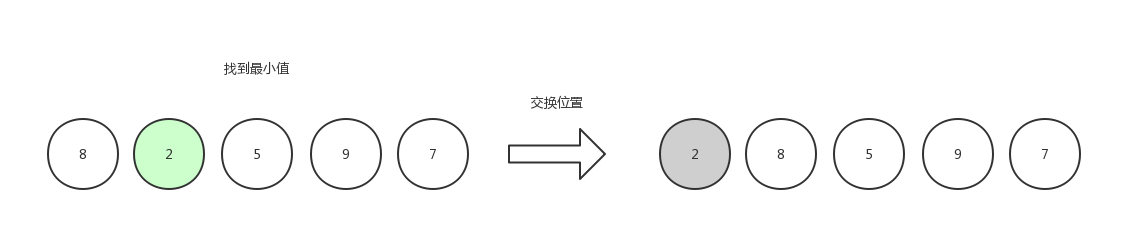
第二次选择,由于数组第一个位置已经是有序的,所以只需要查找剩余位置,找到其中最小的数字5,然后和数组第二个位置的元素交换。
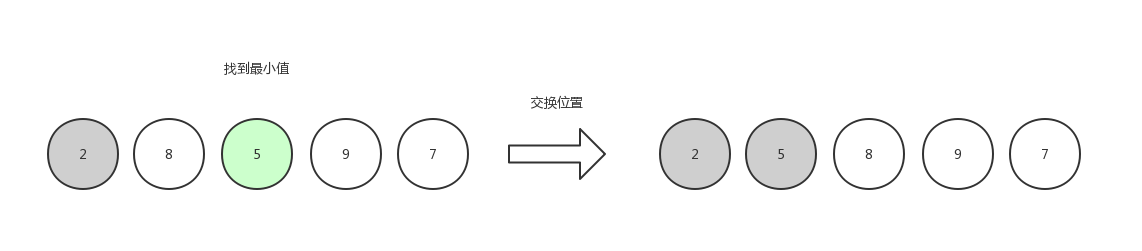
第三次选择,找到最小值 7 ,和第三个位置的元素交换位置。
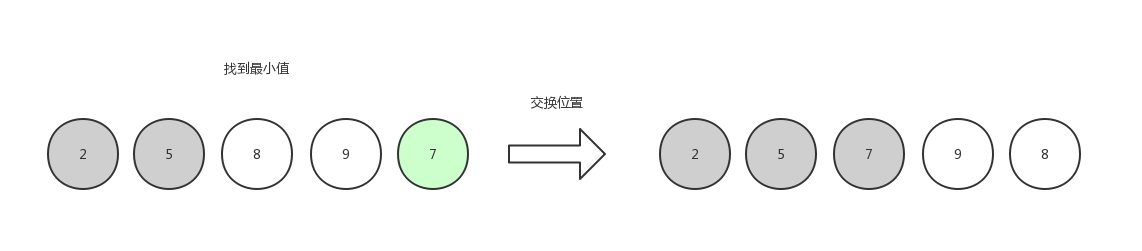
第四次选择,找到最小值8,和第四个位置的元素交换位置。
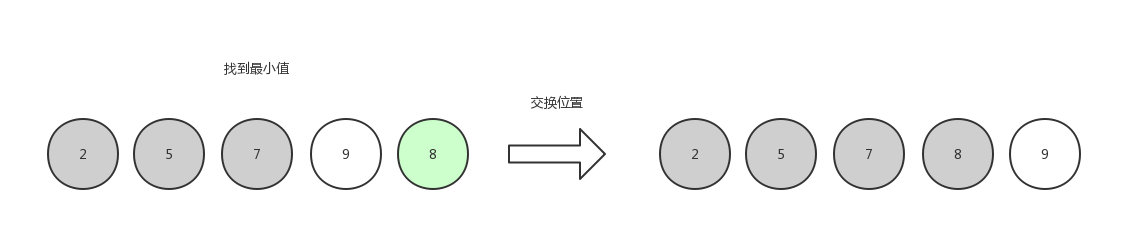
最后一个到达了数组末尾,没有可对比的元素,结束选择。
如此整个数组就排序完成了。
性能
Time Complexity: $O(n^2)$ as there are two nested loops.
Auxiliary Space: $O(1)$
The good thing about selection sort is it never makes more than O(n) swaps and can be useful when memory write is a costly operation.
实现
private static int[] selectionSort(int[] array) {
if (array == null || array.length == 0)
return null;
int minIndex;
for(int i = 0; i< array.length - 1;i++) {
minIndex = i;
for (int j = i+1; j < array.length; j++) {
if(array[j] > array[minIndex]){
minIndex = j;
}
}
if(minIndex != i){
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
}
return array;
}
动画演示
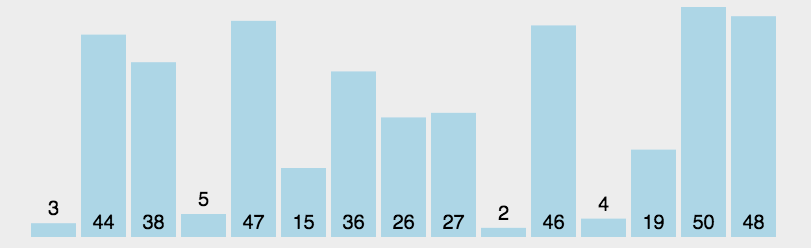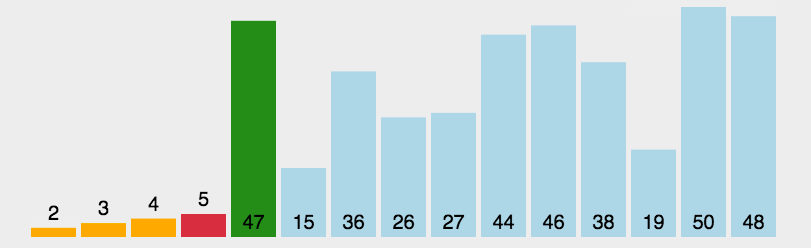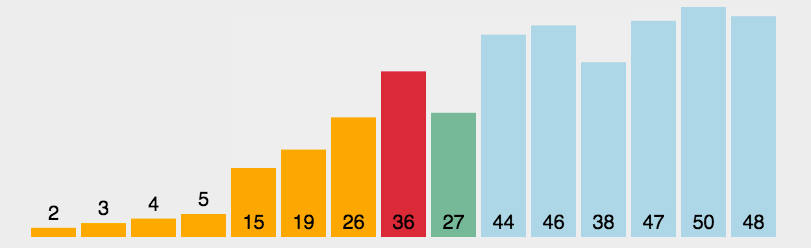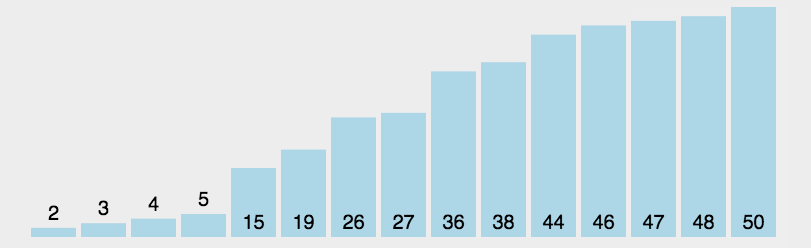
Reference
- GeeksforGeeks Selection Sort - https://www.geeksforgeeks.org/selection-sort/
- https://visualgo.net/en/sorting
- 这或许是东半球讲十大排序算法最好的一篇文章 - https://cxyxiaowu.com/articles/2019/06/11/1560233679033.html