堆排序(Heap Sort)
堆排序是利用**二叉堆(Binary Heap)这种数据结构而设计的一种排序算法,堆排序是一种选择排序,**它的最坏,最好,平均时间复杂度均为$O(nlog_2n)$,它是一种不稳定排序。首先简单了解下堆结构。
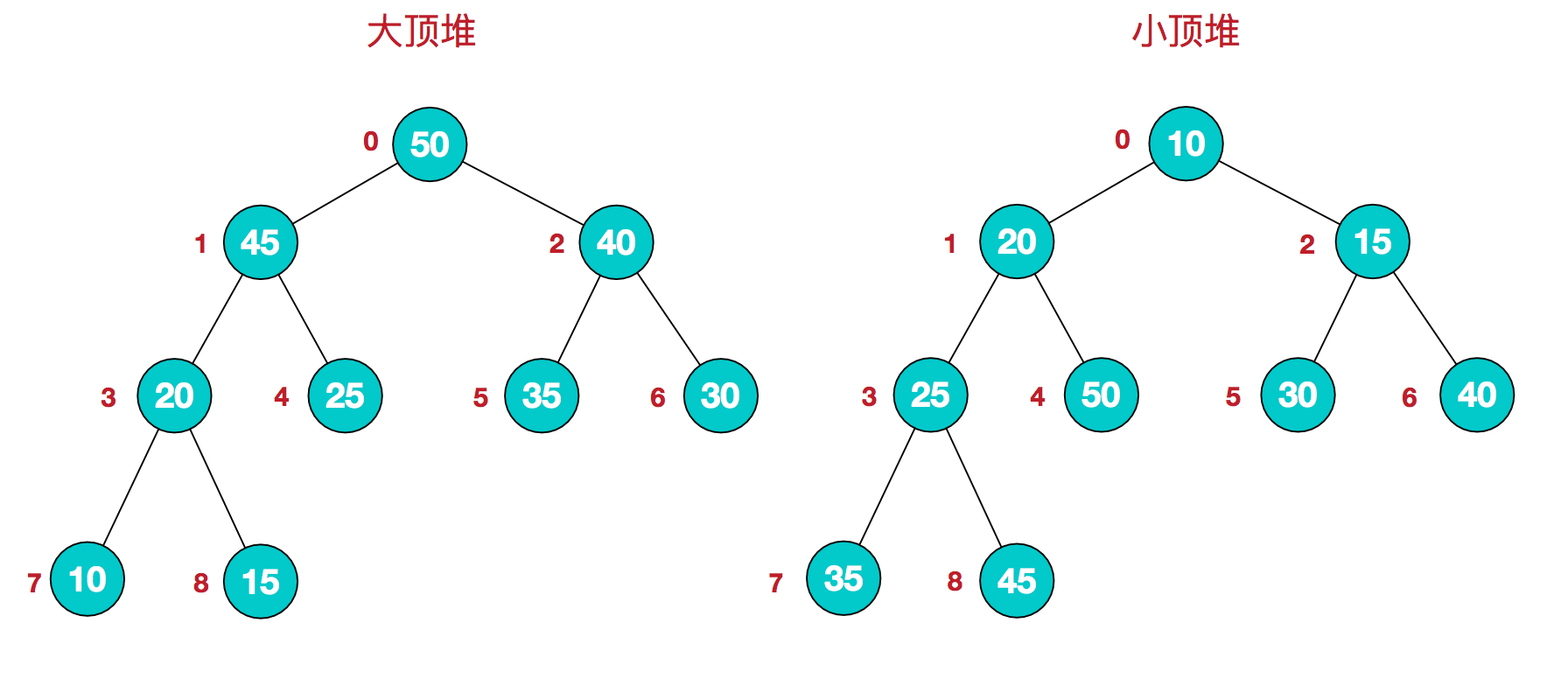
堆是具有以下性质的完全二叉树:
- 每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆(Max Heap);
- 或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(Min Heap)。如下图:
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
- 大顶堆:
arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] - 小顶堆:
arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
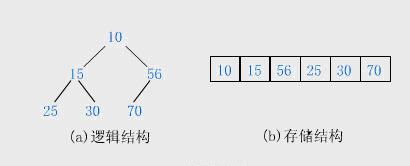
堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i – 1) // 2。它的左右子结点下标分别为2i + 1和 2i + 2。如第0个结点的左右子结点的下标分别为1和2。
堆排序原理
以大顶堆为例,在将无序序列调整成一个大顶堆后,把大顶堆的堆顶元素取出,将取出后剩余的元素继续调整为大顶堆,之后再次将堆顶元素取出,不断重复上面的过程,直到大顶堆中只剩下一个元素后结束。
堆排序步骤
1 构建大顶堆
步骤一 将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
1 假设给定无序序列结构如下
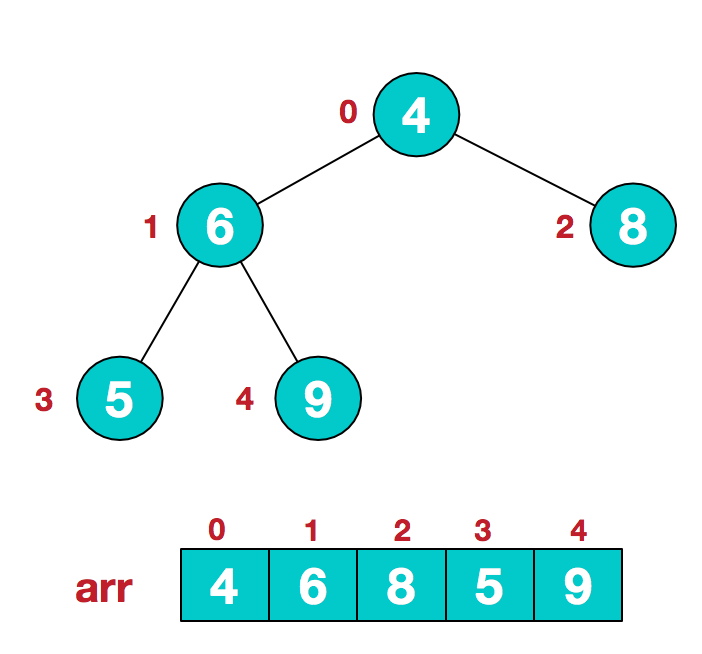
2 此时我们从最后一个非叶子结点开始(即最后一个节点的父节点,该节点索引为 arr.length//2-1=5//2-1=1,也就是结点 6),然后依次从右往左,从下至上进行调整。
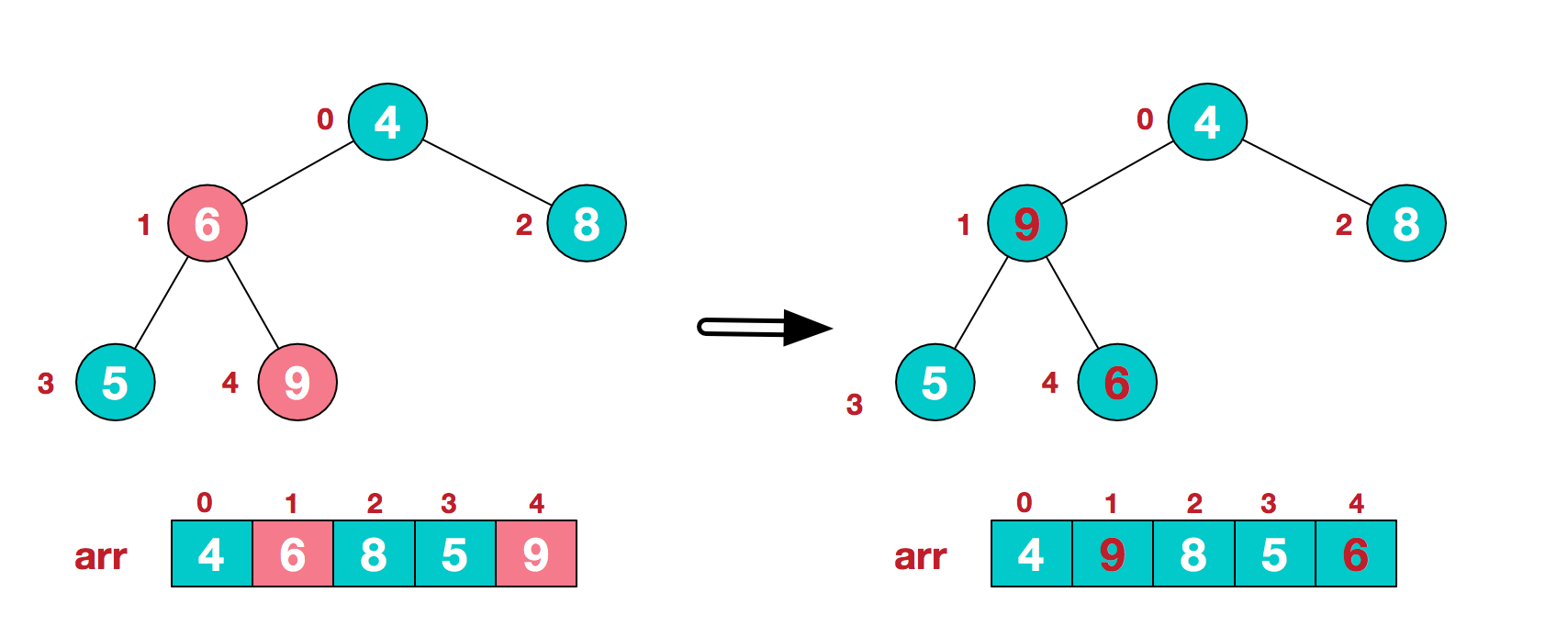
3 找到第二个非叶子节点4,由于[4,9,8]中9元素最大,4和9交换。
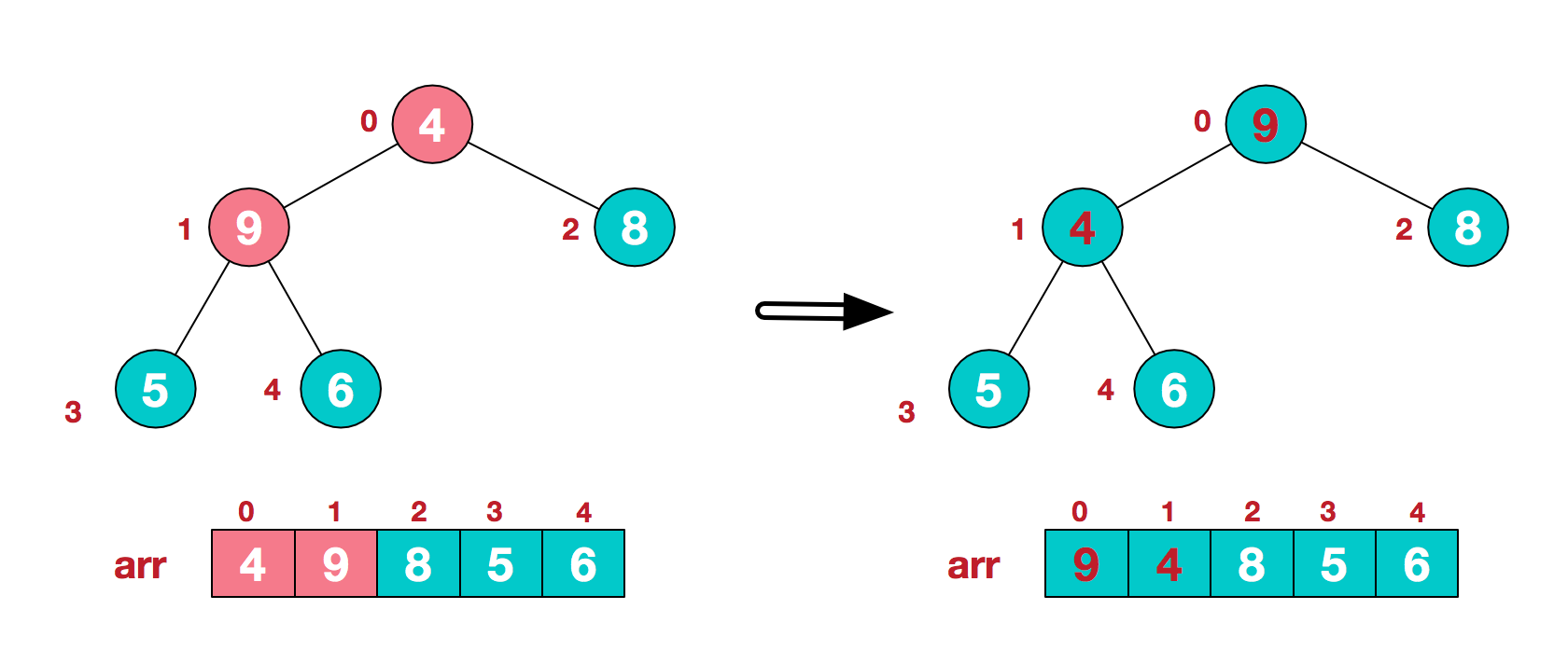
这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
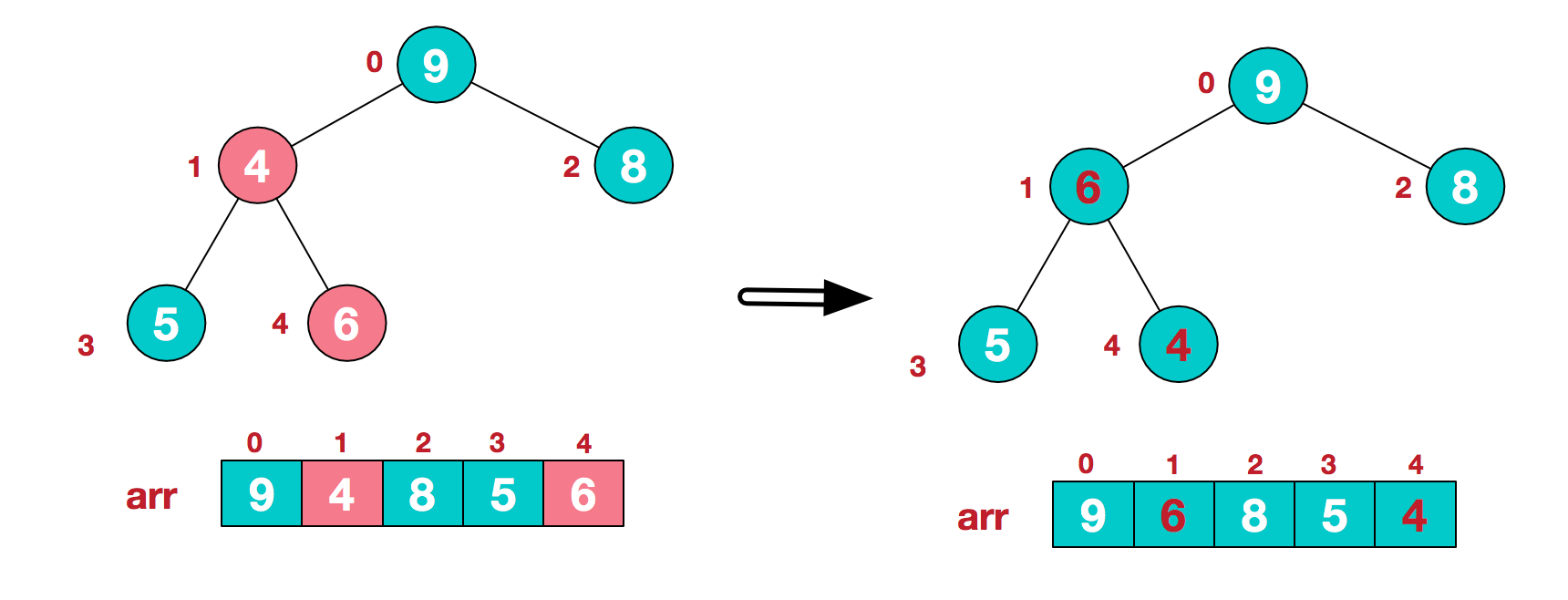
此时,我们就将一个无需序列构造成了一个大顶堆。
2 元素交换,此后不断构建大顶堆
步骤二:将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整当前堆成大顶堆,调整完成后,再将堆顶元素与末尾元素交换,这样得到第二大元素。如此反复进行交换、重建、交换。
1 将堆顶元素9和末尾元素4进行交换
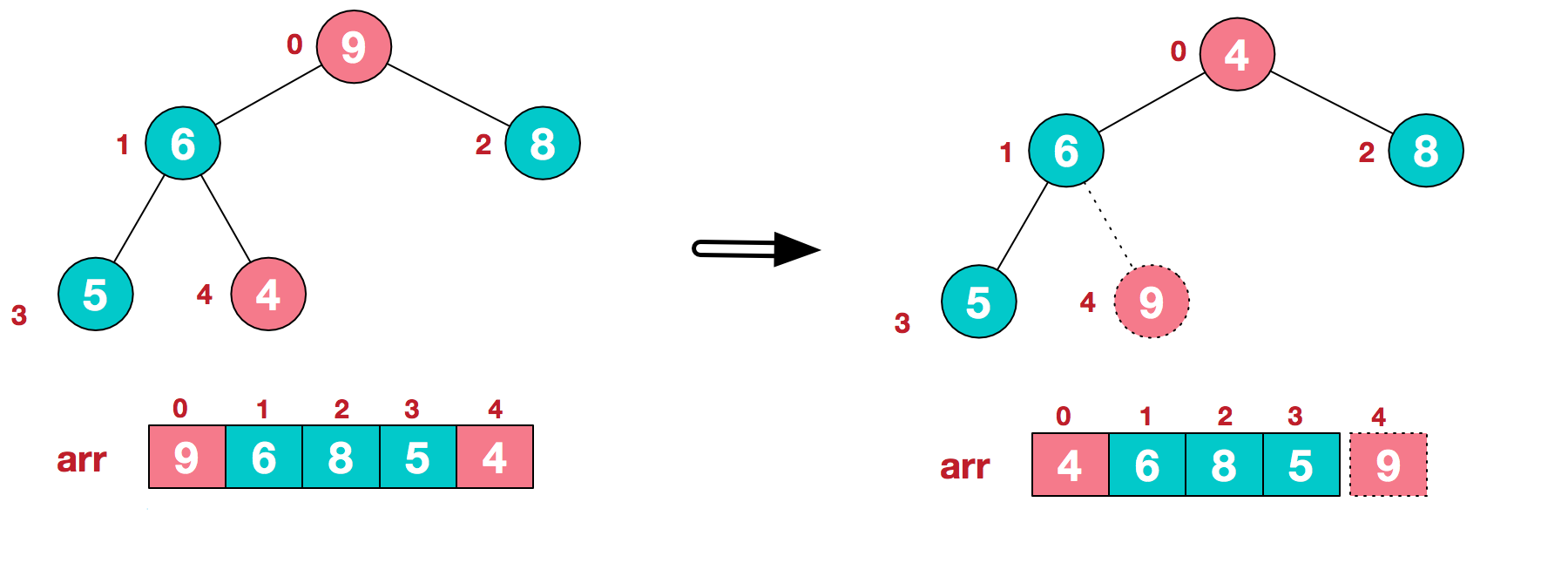
2 重新调整结构,使其继续满足堆定义
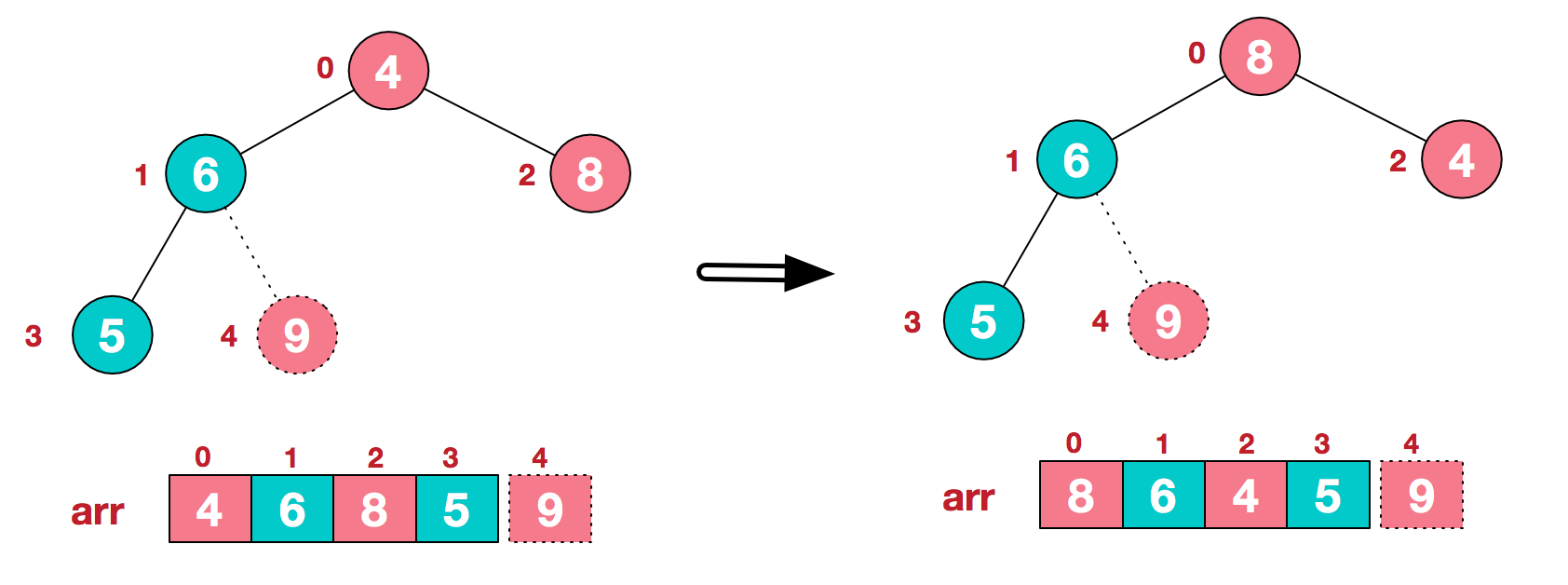
3 再将堆顶元素8 (arr.length-1)/2-1=0 与末尾元素5进行交换,得到第二大元素8
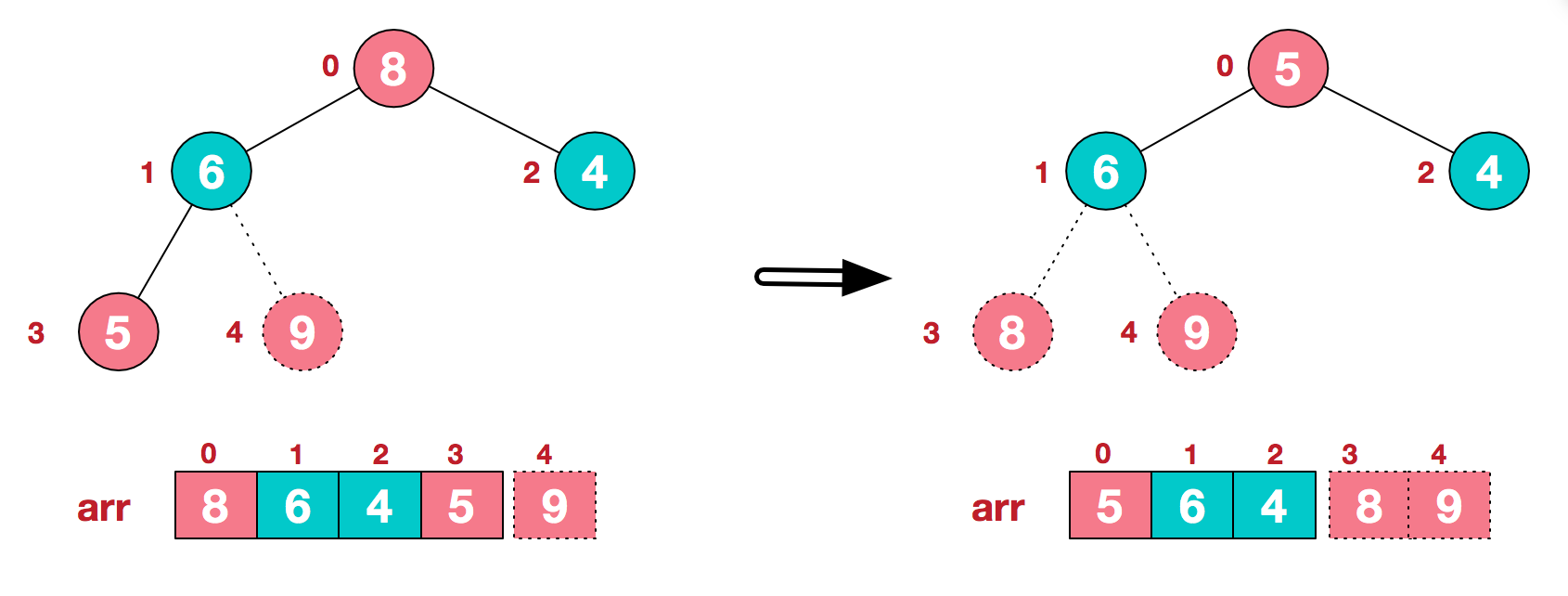
后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
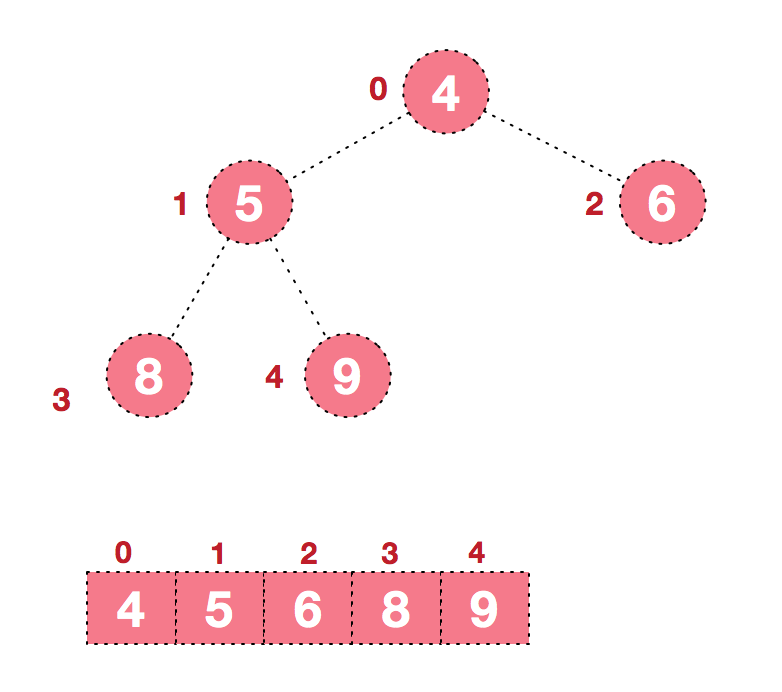
再简单总结下堆排序的基本思路:
- 将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆(假设选择大顶堆);
- 构建大顶堆完成后,将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
- 重新调整结构,使其满足大顶堆的定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序(此时排序后,最小元素在序列的头部)。
Implementation
Java
// Java program for implementation of Heap Sort
public class HeapSort
{
public static void sort(int arr[])
{
int n = arr.length;
// Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// One by one extract an element from heap
for (int i=n-1; i>=0; i--)
{
// Move current root to end
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// call max heapify on the reduced heap
heapify(arr, i, 0);
}
}
// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
static void heapify(int arr[], int n, int i)
{
int largest = i; // Initialize largest as root
int l = 2*i + 1; // left = 2*i + 1
int r = 2*i + 2; // right = 2*i + 2
// If left child is larger than root
if (l < n && arr[l] > arr[largest])
largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest])
largest = r;
// If largest is not root
if (largest != i)
{
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
}
Python
def heapify(arr, n, i):
largest = i # Initialize largest as root
left = 2 * i + 1 # left child
right = 2 * i + 2 # right child
# See if left child of root exists and is greater than root
if left < n and arr[i] < arr[left]:
largest = left
# See if right child of root exists and is greater than root
if right < n and arr[largest] < arr[right]:
largest = right
# Change root, if needed
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # swap
# Heapify the root.
heapify(arr, n, largest)
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# One by one extract elements
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # swap
heapify(arr, i, 0)
# Example usage
arr = [12, 11, 13, 5, 6, 7]
heapSort(arr)
print("Sorted array is:", arr)
Complexity
- Worst-Case Complexity: O(nlog n)
- Best-Case Complexity: O(n log n)
- Average-Case Complexity: O(nlogn)
- Space Complexity: O(1)
Reference
- 常见排序算法 - 堆排序 (Heap Sort) - http://bubkoo.com/2014/01/14/sort-algorithm/heap-sort/
- HeapSort - https://www.geeksforgeeks.org/heap-sort/
- 算法从入门到“放弃”(10)- 堆排序 - https://zhuanlan.zhihu.com/p/45725214
- 【图解数据结构】一组动画彻底理解堆排序 - https://mp.weixin.qq.com/s?__biz=MzUyNjQxNjYyMg==&mid=2247484004&idx=1&sn=ecbafdec3c38ac7a13979aace18569e4&chksm=fa0e6de5cd79e4f3b059d507ac0c6bf9ec916711891f0e92377f0d4bcf9d24319d09ed68d990&scene=21#wechat_redirect
- 这或许是东半球讲十大排序算法最好的一篇文章 - https://cxyxiaowu.com/articles/2019/06/11/1560233679033.html