模式匹配/ 字符串匹配算法
字符串匹配
字符串匹配问题的形式定义:
- **文本(Text)**是一个长度为 n 的数组 T[1..n];
- **模式(Pattern)**是一个长度为 m 且 m≤n 的数组 P[1..m];
- T 和 P 中的元素都属于有限的字母表 Σ 表;
- 如果 0≤s≤n-m,并且 T[s+1..s+m] = P[1..m],即对 1≤j≤m,有 T[s+j] = P[j],则说模式 P 在文本 T 中出现且位移为 s,且称 s 是一个有效位移(Valid Shift)。
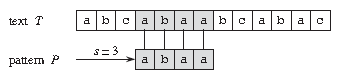
比如上图中,目标是找出所有在文本 T = abcabaabcabac 中模式 P = abaa 的所有出现。该模式在此文本中仅出现一次,即在位移 s = 3 处,位移 s = 3 是有效位移。
常见的字符串匹配算法
解决字符串匹配的算法包括:朴素算法(Naive Algorithm)、Rabin-Karp 算法、有限自动机算法(Finite Automation)、 Knuth-Morris-Pratt 算法(即 KMP Algorithm)、Boyer-Moore 算法、Simon 算法、Colussi 算法、Galil-Giancarlo 算法、Apostolico-Crochemore 算法、Horspool 算法和 Sunday 算法等。
字符串匹配算法的步骤
字符串匹配算法通常分为两个步骤:预处理(Preprocessing)和匹配(Matching)。所以算法的总运行时间为预处理和匹配的时间的总和。
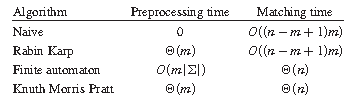
上图描述了常见字符串匹配算法的预处理和匹配时间。
朴素的字符串匹配算法(Naive String Matching Algorithm)
朴素的字符串匹配算法(Naive String Matching Algorithm),又称为暴力匹配算法(Brute Force Algorithm):对主串(S)的每一个字符作为子串(T)开头,与要匹配的字符串进行匹配。对主串做大循环,每个字符开头做T的长度的小循环,直到匹配成功或全部遍历完成为止。
它的主要特点是:
- 没有预处理阶段;
- 滑动窗口总是后移 1 位;
- 对模式中的字符的比较顺序不限定,可以从前到后,也可以从后到前;
- 匹配阶段需要 O((n - m + 1)m) 的时间复杂度;
- 需要 2n 次的字符比较;
很显然,朴素的字符串匹配算法 NAIVE-STRING-MATCHER 是最原始的算法,它通过使用循环来检查是否在范围 n-m+1 中存在满足条件 P[1..m] = T [s + 1..s + m] 的有效位移 s。
例子
首先,将串 A 与串 B 的首字符对齐,然后逐个判断相对的字符是否相等,如下图所示:
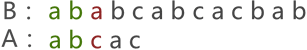
上图中,由于串 A 与串 B 的第 3 个字符匹配失败,因此需要将串 A 后移一个字符的位置,继续同串 B 匹配,如下图所示:
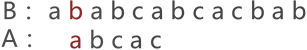
上图中可以看到,两串匹配失败,串 A 继续向后移动一个字符的位置,如下图所示:
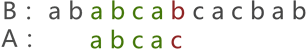
上图中,两串的模式匹配失败,串 A 继续移动,一直移动至下图的位置才匹配成功:

由此,串 A 与串 B 以供经历了 6 次匹配的过程才成功,通过整个模式匹配的过程,证明了串 A 是串 B 的子串(串 B 是串 A 的主串)。
时间复杂度
假设模式P的长度为n,文本T的长度为m,匹配的时间在最好情况下为Θ(n),在最坏情况下为 Θ((n-m+1)m),如果 m = [n/2],则为 Θ(n2)。
Java实现
public static int naiveStringMatch(String text, String pattern) {
char[] textChs = text.toCharArray();
char[] patternChs = pattern.toCharArray();
int i = 0, j = 0;
for (i = 0; i < textChs.length - patternChs.length; i++) {
for (j = 0; j < patternChs.length; j++) {
if (textChs[i + j] != patternChs[j]) {
break;
}
}
if (j == patternChs.length) {
return i;
}
}
return -1;
}
Reference
- 数据结构-串 - https://zhuanlan.zhihu.com/p/29160321
- 数据结构之串 - https://www.zybuluo.com/guoxs/note/237408
- [数据结构]线性结构——串 - https://blog.csdn.net/shimazhuge/article/details/46808193
- 字符串匹配算法 - https://www.cnblogs.com/gaochundong/p/string_matching.html