主要分类

0-1背包

每个物品只能取一次

Leetcode：

Leetcode 474. Ones and Zeroes（01背包）

爆搜解法

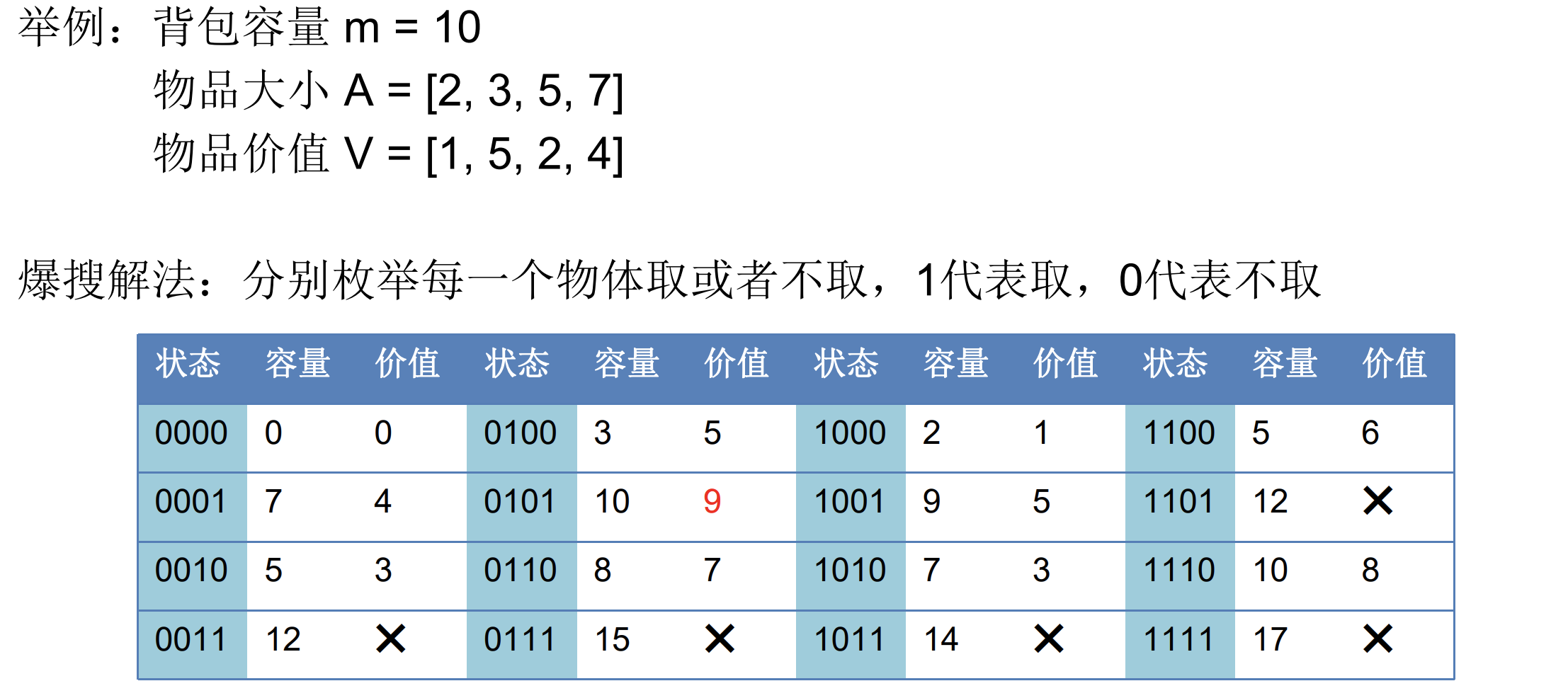
用 4 个 bit 分别标识 4 种物品，取还是不取。

贪心法 - 错误解

所有的贪心，都是错误的！！！

反例：

取价值最高

m=2, A = [1, 1, 2], V = [2, 2, 3] •

贪心答案：3，正确答案：4

取重量最轻

m=2, A = [1, 1, 2], V = [1, 1, 3]

贪心答案：2，正确答案

取单位价值最高

m=3, A = [1, 1, 3], V = [2, 2, 5]

贪心答案：4，正确答案：5

爆搜算法的局限

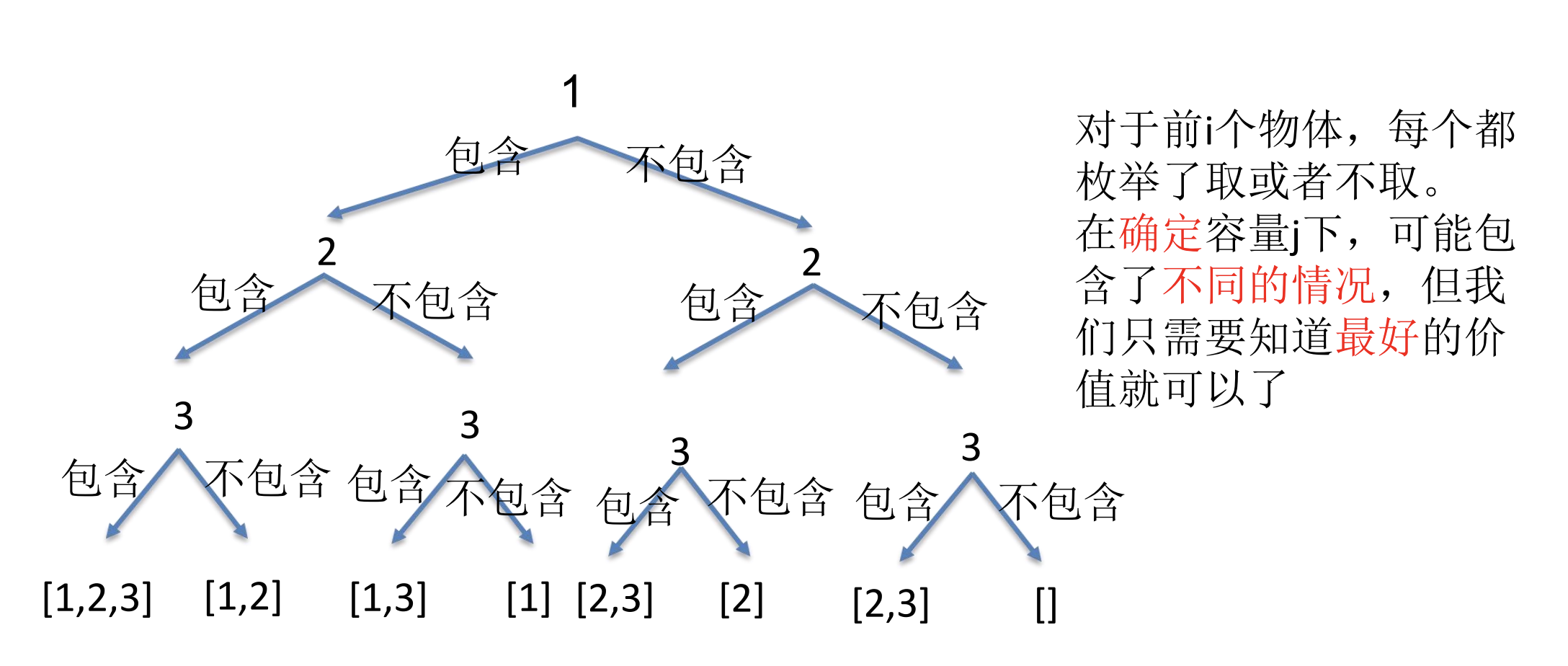
动态规划解法

举例1：

背包容量 m = 10

物品大小 A = [2, 3, 5, 7]

物品价值 V = [1, 5, 2, 4]

使用数组来记录可取前i个物品，在容量j的情况下能取的最大价值

i/j	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0
1	1	1	1	1	1	1	1	1	1
2	1	5	5	6	6	6	6	6	6
3	1	5	5	6	6	6	7	7	8
4	1	5	5	6	6	6	7	7	9

dp[i][j]表示前i个物体，在容量j的情况下，能取到的最大价值：

如果取第i个物体，价值为dp[i - 1][j - A[i]] + V[i] (j-A[i]>0)
如果不取第i个物体，价值为dp[i - 1][j] 状态转移：dp[i][j] = max(dp[i - 1][j – A[i]] + V[i], dp[i - 1][j])

public static int backPackII(int m, int[] A, int[] V) {
    int[][] maxs = new int[A.length + 1][m + 1];

    for (int i = 0; i < maxs.length; i++) {
        for (int j = 0; j < maxs[0].length; j++) {
            if (i == 0 || j == 0)
                maxs[i][j] = 0;
            else if (j < A[i - 1]) {
                maxs[i][j] = maxs[i - 1][j];
            } else {// j>=A[i-1]
                maxs[i][j] = Math.max(V[i - 1] + maxs[i - 1][j - A[i - 1]], maxs[i - 1][j]);

            }
        }
    }

    return maxs[A.length][m];
}

完全背包

每个物品能取无穷次

多重背包

每一个物品都只有有限数量

FEATURED TAGS

algorithm algorithmproblem architecturalpattern architecture aws c# cachesystem codis compile concurrentcontrol database dataformat datastructure debug design designpattern distributedsystem django docker domain engineering freebsd git golang grafana hackintosh hadoop hardware hexo http hugo ios iot java javaee javascript kafka kubernetes linux linuxcommand linuxio lock macos markdown microservices mysql nas network networkprogramming nginx node.js npm oop openwrt operatingsystem padavan performance programming prometheus protobuf python redis router security shell software testing spring sql systemdesign truenas ubuntu vmware vpn windows wmware wordpress xml zookeeper

【Algorithm】动态规划 - 背包问题