B树(B-tree)
在计算机科学中,B树(B-tree)是一种树状数据结构,它能够存储数据、对其进行排序并允许以$O(log_2n)$的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树,概括来说是一个节点可以拥有多于2个子节点的平衡查找树,因为其一个节点可以拥有多于2个子节点,因而也可以称为多路自平衡查找树(Multi-way Self-balancing Search Tree),简称为多路查找树。
B 树是一种广为使用的读优化索引数据结构,是二叉树的一种泛化。它具有多种变体,并已用于多种数据库(包括MySQL InnoDB4和PostgreSQL7)和文件系统(例如,HFS+8、ext4 中的 HTrees9)。B 树中的“B”表示“Bayer”,指的是数据结构的最初创立者 Rudolf Bayer,也可以说是 Bayer 彼时供职的波音公司(Boeing)。
与自平衡二叉查找树(Self-balancing Binary Search Tree)不同,B-树为系统最优化大块数据的读和写操作。B树减少定位记录时所经历的中间过程,从而加快存取速度。普遍运用在数据库和文件系统。”
总的来说,B/B+树是为了磁盘或其它存储设备而设计的一种多路自平衡查找树(多路自平衡查找树的"多路",是相对于"二叉”而言,即B树的一个节点,可以有多个子树,或者说子节点)。与红黑树相比,在相同的的节点的情况下,一颗B/B+树的高度远远小于红黑树的高度。B/B+树上操作的时间通常由存取磁盘的时间和CPU计算时间这两部分构成,而CPU的速度非常快,所以B树的操作效率取决于访问磁盘的次数,关键字总数相同的情况下,B树的高度越小,磁盘I/O所花的总时间越短(因为访问磁盘的次数越少)。
B 树可以看作是对2-3查找树的一种扩展, where each internal node may have only 2 or 3 child nodes.
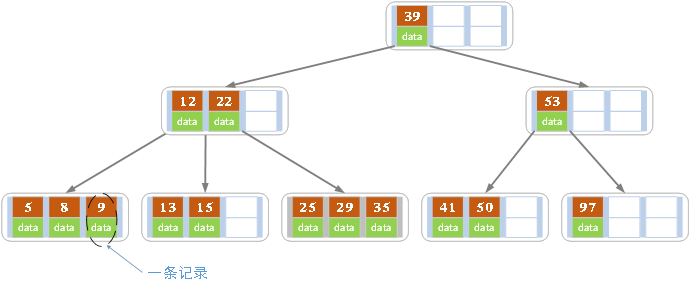
在B树中,一条数据元素记录为一个二元组[key, data],key为记录的键值,对于不同数据记录,key是互不相同的;data为数据记录除key外的数据。
假设一棵B树的阶/度(degree/ branching factor)为M,则:
- 子节点:
- 对于根节点,子树个数范围为0或[2,M];
- 除了根节点和叶子节点外,每个节点最多有M个孩子,至少有ceil(M/2)个孩子(注:ceil()是朝正无穷方向取整的函数,如
ceil(1.1)结果为2)。
- 节点的数据元素:
- 每个节点数据元素的个数范围为[1,M-1],并且以升序排列;
- 一个有k个叶子节点的非叶子节点有且只能有k-1个数据元素。
- 其他:
- 所有叶子节点在同一层。
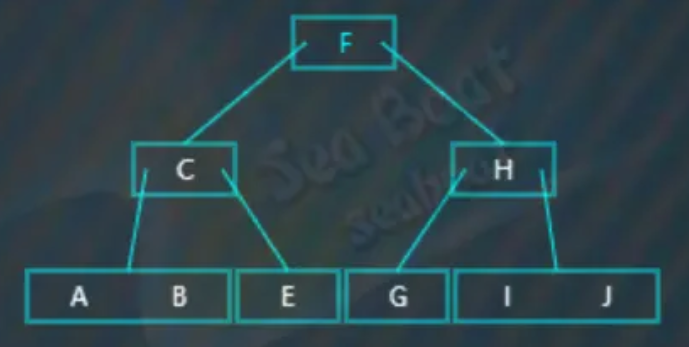
下图是一个d=4的B-Tree:
性能
一个度为d的B-Tree,设其索引了N个key(或者说,它包含了N个数据元素),则其树高h的上限为$log_d((N+1)/2)$,检索一个key,其查找节点个数的渐进复杂度为$O(log_dN)$。从这点可以看出,B-Tree是一个非常有效率的索引数据结构。
操作
插入操作
例子1
下面以一个5阶B树为例,介绍B树的插入操作,在5阶B树中,节点中最多有4个数据元素。
在空树中插入值为39的数据元素:

此时根节点就1个数据元素,此时根节点也是叶子节点。
继续依次插入值分别为22,97和41的数据元素:

根节点此时有4个数据元素。
继续插入值为53的数据元素:

插入后超过了一个节点中最大有4个数据元素的个数,所以以值为41的数据元素为中心进行分裂,结果如下图所示,分裂后当前节点指针指向父节点,满足B树条件,插入操作结束。
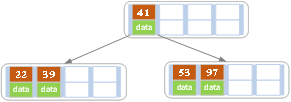
当阶数m为偶数时,需要分裂时就不存在排序恰好在中间的数据元素,那么我们选择中间位置的前一个数据元素或中间位置的后一个数据元素为中心进行分裂即可。
依次插入值分别为13,21,40的数据元素,同样会造成分裂,分裂后结果如下图所示。
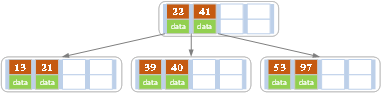
依次插入值分别为27,30,33的数据元素;
再依次插入值分别为36,35,34的数据元素;当插入34后,发生分裂。
再依次插入值分别24,29的数据元素,插入后结果如下图所示:

插入值为26的数据元素,插入后的结果如下图所示。

当前节点需要以值为27的数据元素为中心分裂,并向父节点进位27,然后当前节点指向父节点,结果如下图所示。

进位后导致当前节点(即根节点)也需要分裂,分裂后的结果如下图所示:
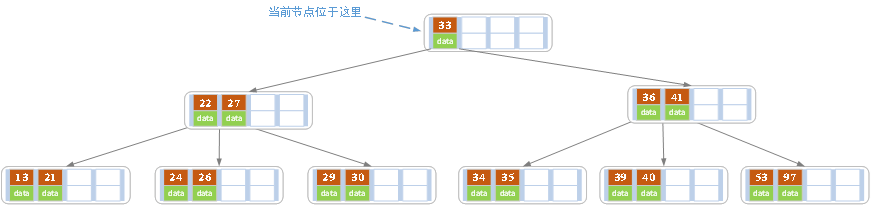
分裂后当前节点指向新的根,此时无需调整。
最后再依次插入值分别为17,28,29,31,32的的数据元素,当插入32时,发生分裂,分裂后的结果如下图所示:

例子2
假设现在构建一棵四阶B树,开始插入“A”,直接作为根节点,
插入“B”,大于“A”,放右边,
插入“C”,按顺序排到最后,
继续插入“D”,直接添加的结果如下图,此时超过了节点可以存放容量,对于四阶B树每个节点最多存放3个值,此时需要执行分裂操作,
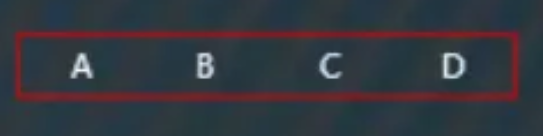
分裂操作为,先选取待分裂节点的中值,这里为“B”,然后将中值“B”放到父节点中,因为这里还没有父节点,那么直接创建一个新的父节点存放“B”,而原来小于“B”的那些值作为左子树,原来大于“B”的那些值作为右子树。
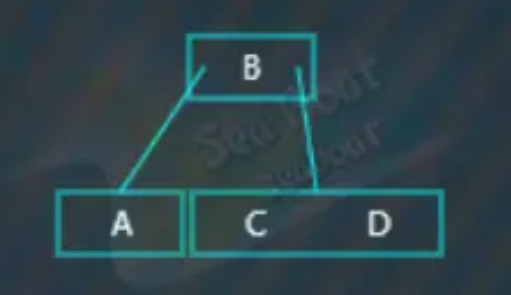
继续插入“E”,“E"大于“B”,往右子节点,
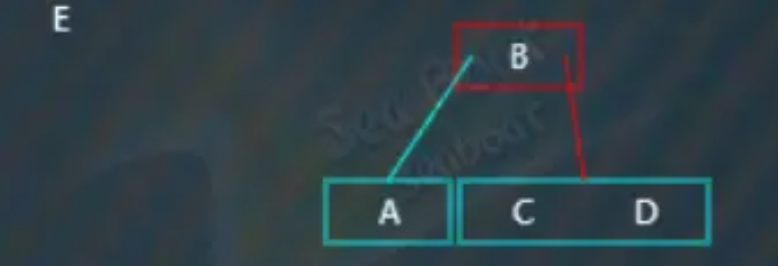
分别于“C”和“D”比较,大于它们,放到最右边,
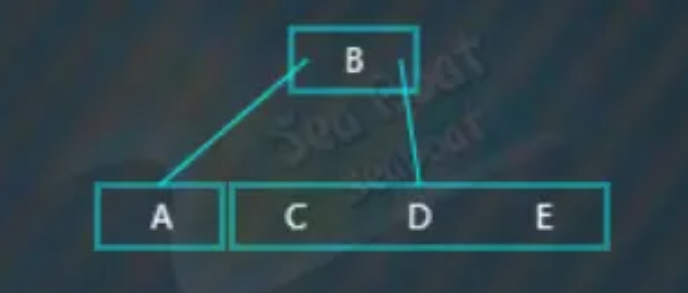
插入“F”,“F”大于“B”,往右子树,
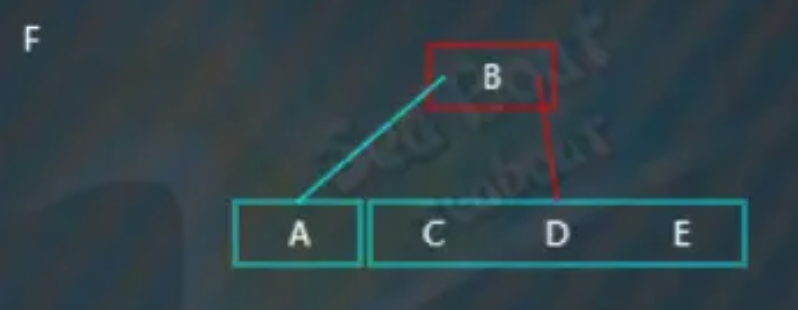
“F”分别与“C”“D"“E"比较,大于它们,放到最右边,此时触发分裂操作,
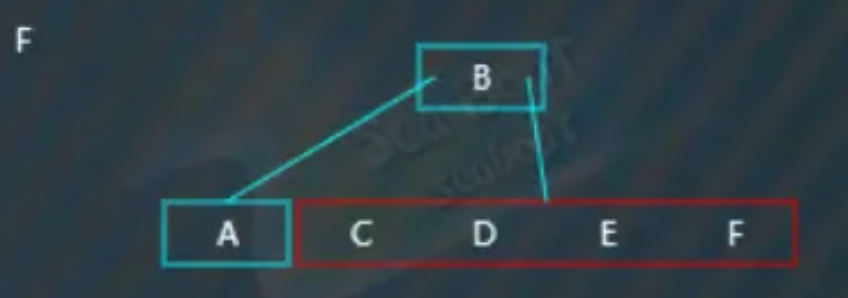
选取待分裂节点的中值“D”,然后将中值“D”放到父节点中,父节点中的“B”小于“D”,于是放到“B”右边,而原来小于“D”的那些值作为左子树,原来大于“D”的那些值作为右子树。
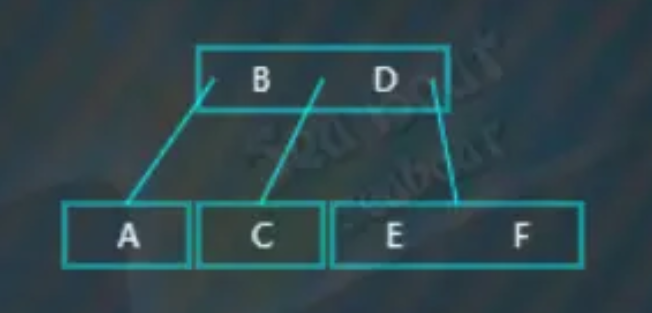
继续插入“M”,结果为,
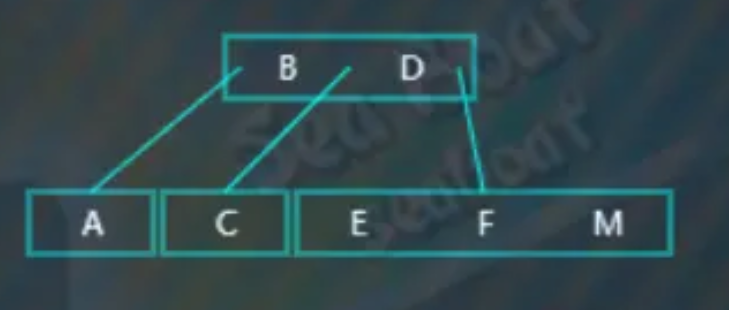
插入“L’,大于“B”“D”,往右子树,
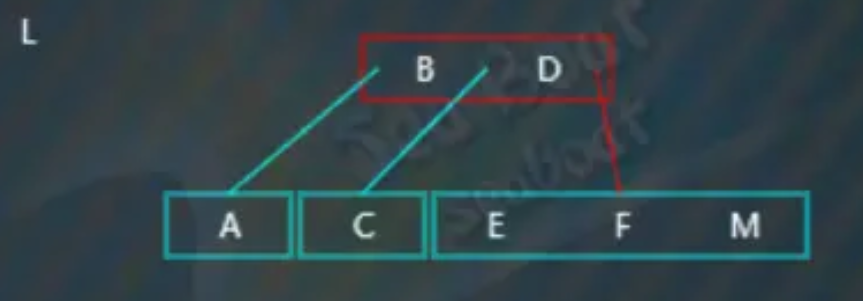
“L”大于“E”“F”小于“M”,于是放到第三个位置,此时触发分裂操作,
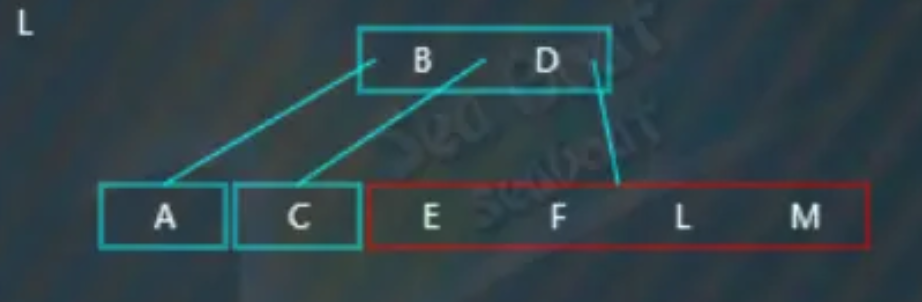
选取待分裂节点的中值“F”,然后将中值“F”放到父节点中,父节点中的“B”“D”都小于“F”,于是放到最右边,而原来小于“F”的那些值作为左子树,原来大于“F”的那些值作为右子树。
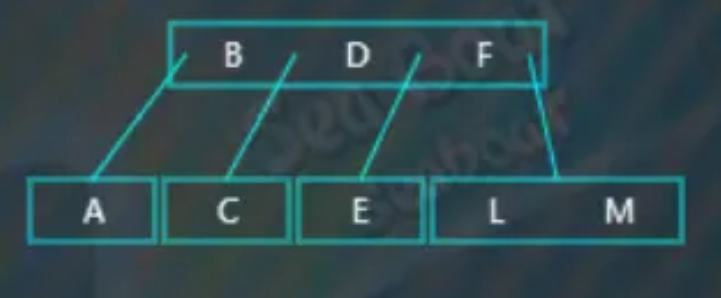
插入“K”,结果为,

插入“J”,大于“B”“D”“F”,往右子树,
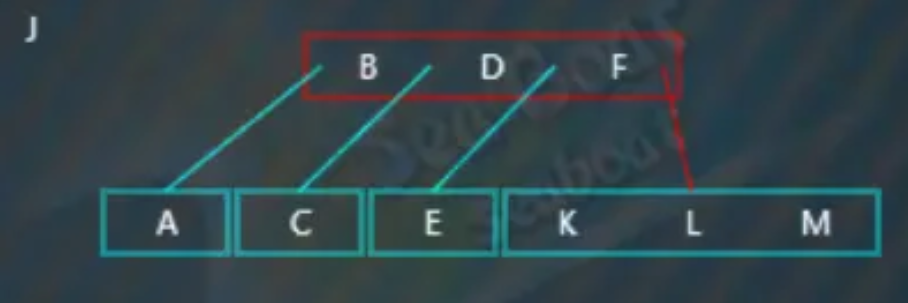
“J”小于“K”“L”“M”,于是放到第一个位置,此时触发分裂操作,
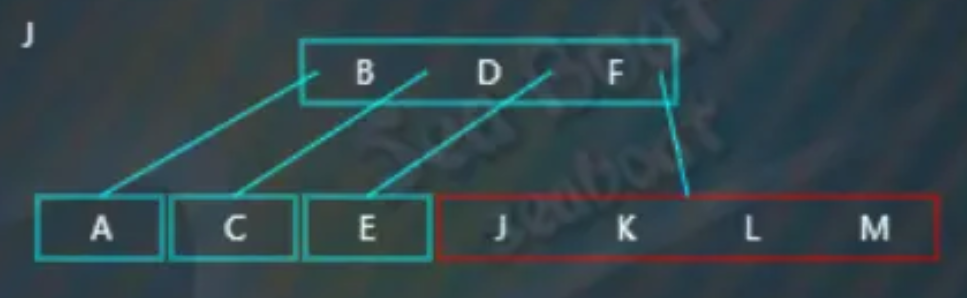
选取待分裂节点的中值“K”,然后将中值“K”放到父节点中,父节点中的“B”“D”“F”都小于“K”,于是放到最右边,而原来小于“K”的那些值作为左子树,原来大于“K”的那些值作为右子树。此时父节点也触发分裂操作,

选取待分裂节点的中值“D”,然后将中值“D”放到父节点中,由于还没有父节点,那么直接创建一个新的父节点存放“D”,而原来小于“D”的那些值作为左子树,原来大于“D”的那些值作为右子树。

插入“I”,大于“D”,往右子树,
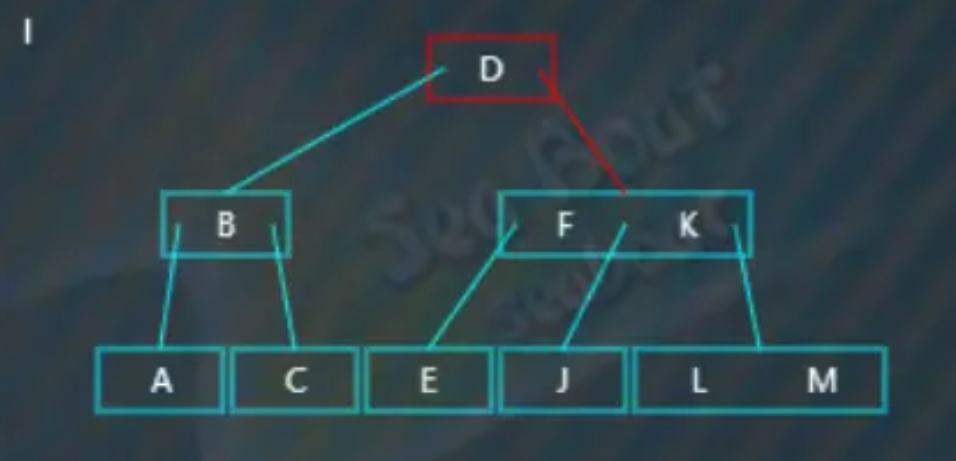
右子树不是叶子节点,继续往下,这时“I”大于“F”而小于“K”,所以往第二个分支,
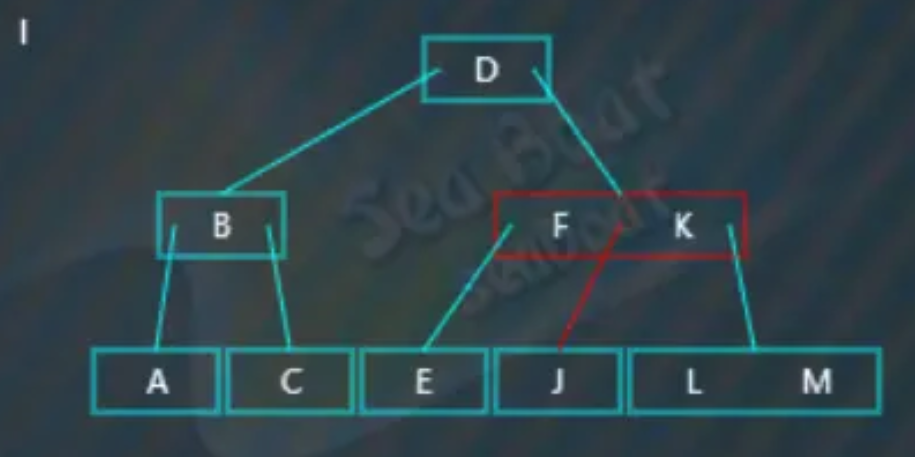
“I”小于“J”,于是放到左边,
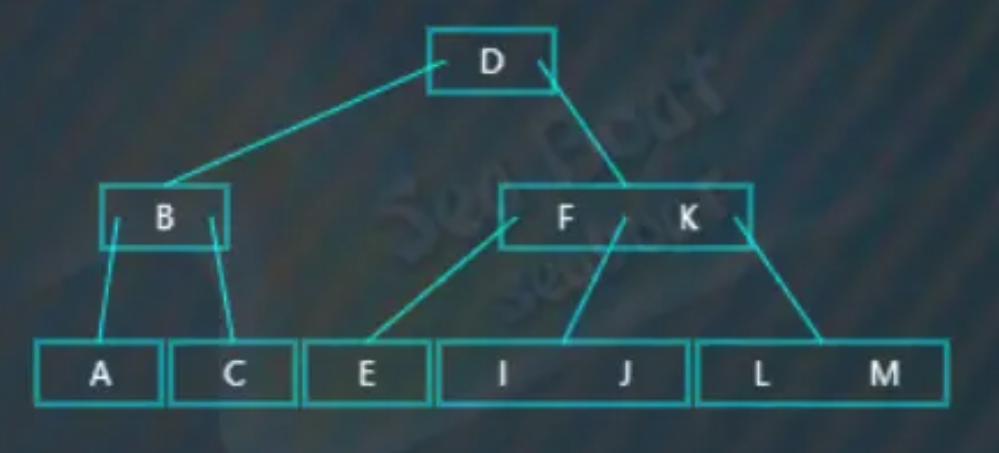
类似地,插入“H”,结果如下,
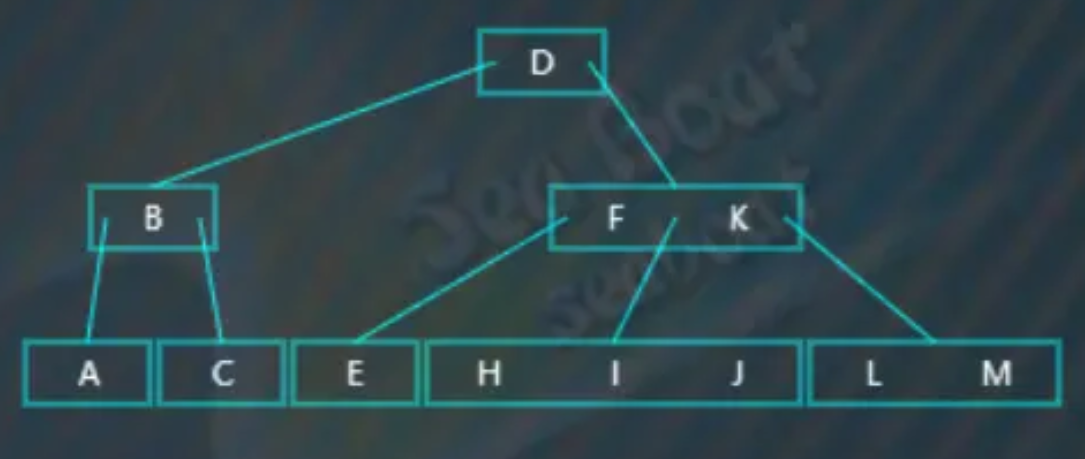
插入“G”,往右子树,
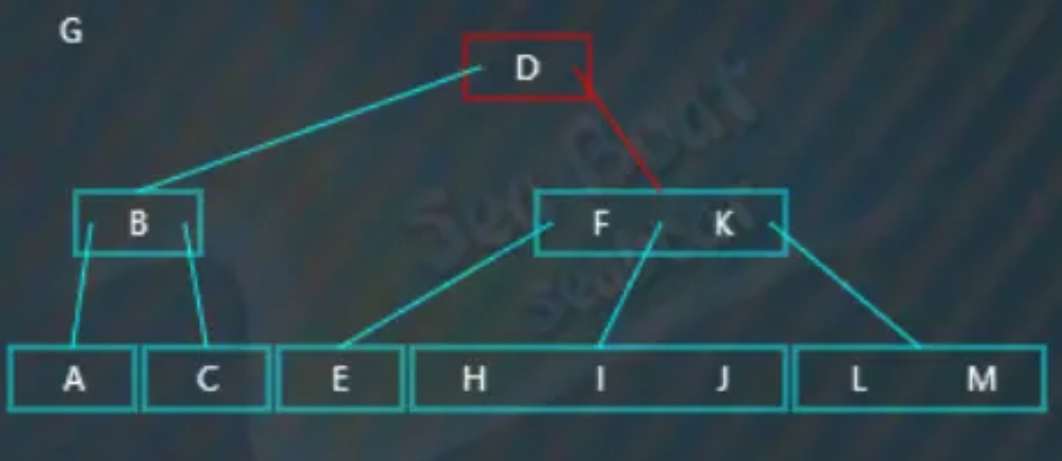
往中间分支,
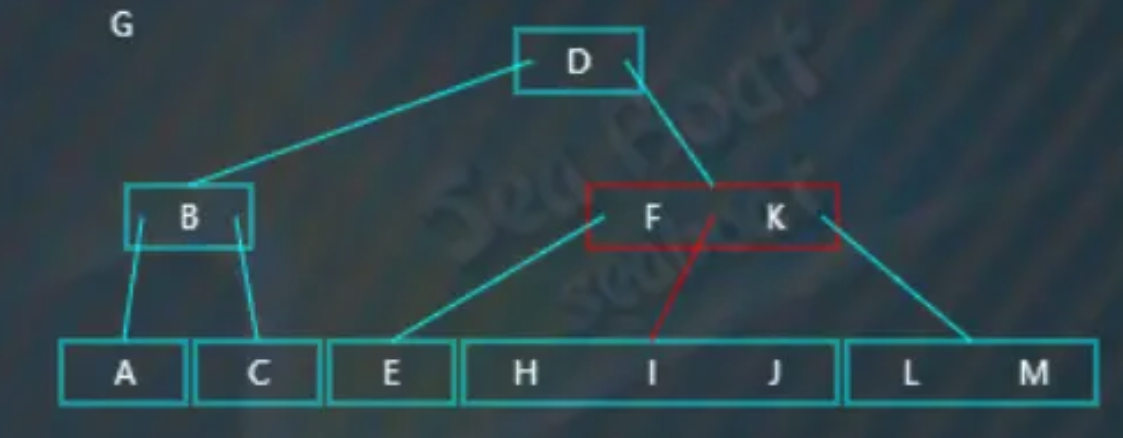
触发分裂操作,
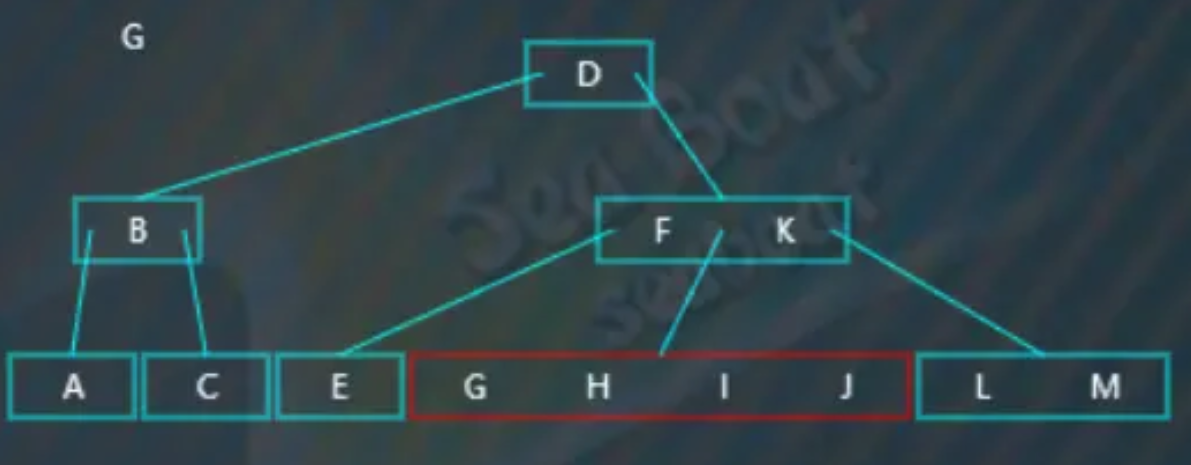
选取待分裂节点的中值“H”,然后将中值“H”放到父节点中,“H"大于父节点中的“F”而小于“K”,于是放到中间,而原来小于“H”的那些值作为左子树,原来大于“H”的那些值作为右子树。
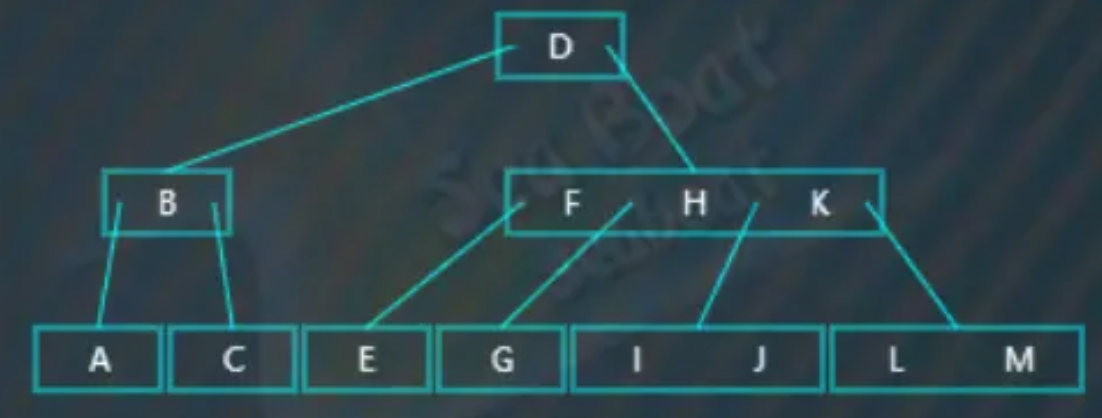
综上所述,插入操作的核心是分裂操作。无需分裂的情况比较简单,直接插入即可;如果插入后超过节点容量,这个容量可预先自定义,则需要进行分裂操作,需要注意的是分裂可能引起父节点需要继续分裂。
查找操作
对B树进行查找就比较简单,查找过程有点类似二叉查找树,从根节点开始查找,根据比较数值找到对应的分支,继续往子树上查找。
比如查找“I”,“I"大于“D”,往右子树,
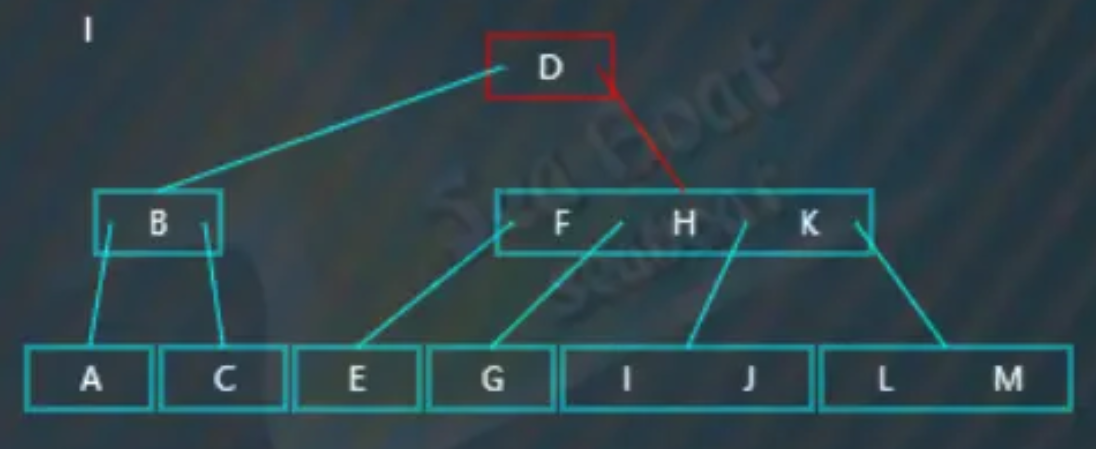
“I”分别与节点内值比较,大于“F”“H”而小于“K”,往第三个分支,
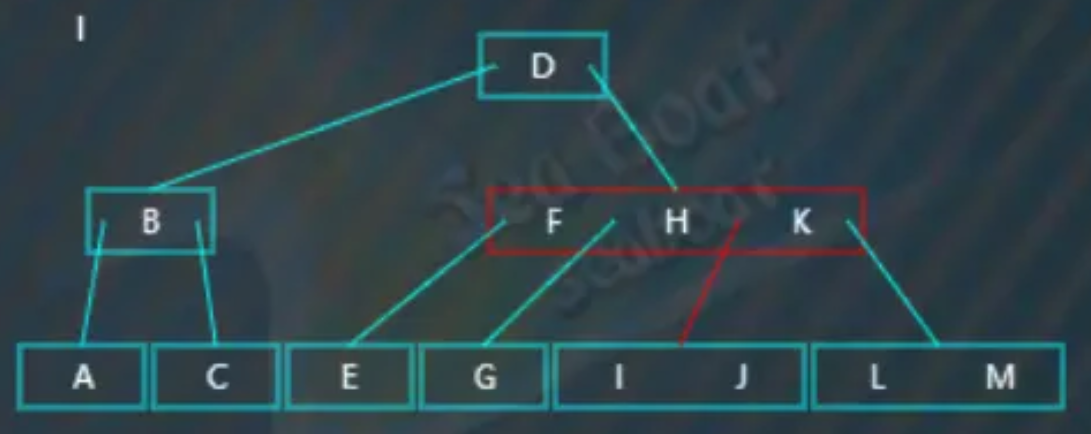
逐一比较节点内的值,找到“I”。
删除操作
删除操作比较复杂,主要是因为删除的值可能在叶子节点上也可能在非叶子节点上,而且删除后可能导致不符合B树的规定,这里暂且称之为导致B树不平衡,于是要进行一些合并、左旋、右旋等操作,使之符合B树的规定(即让B树平衡)。另外,如果是删除非叶子节点的值,则需要先找到中序前驱来替换。
情况一 - 删除叶子元素,不影响平衡
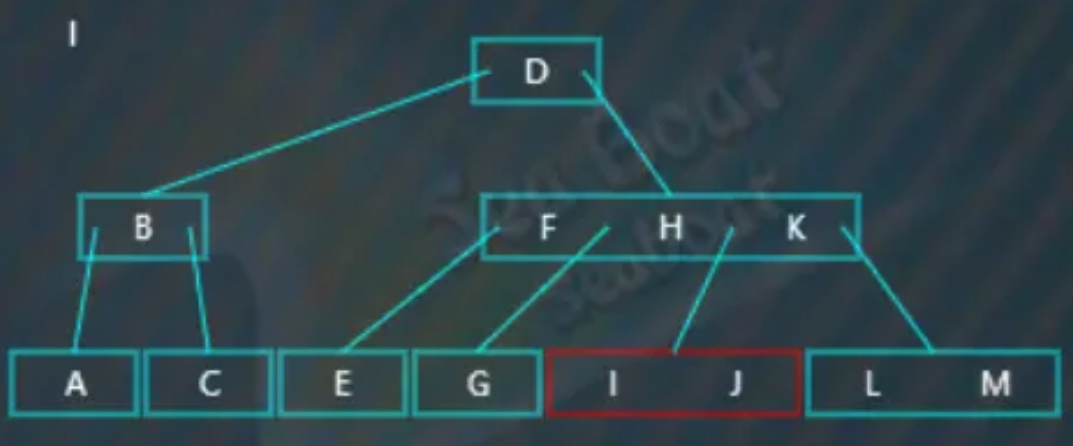
要删除的值在叶子节点上且不影响B树的平衡结构(或者说,这个叶子节点上包含大于等于两个值),比如删除“I”,从根节点开始查找,“I”大于“D”,往第二个分支:
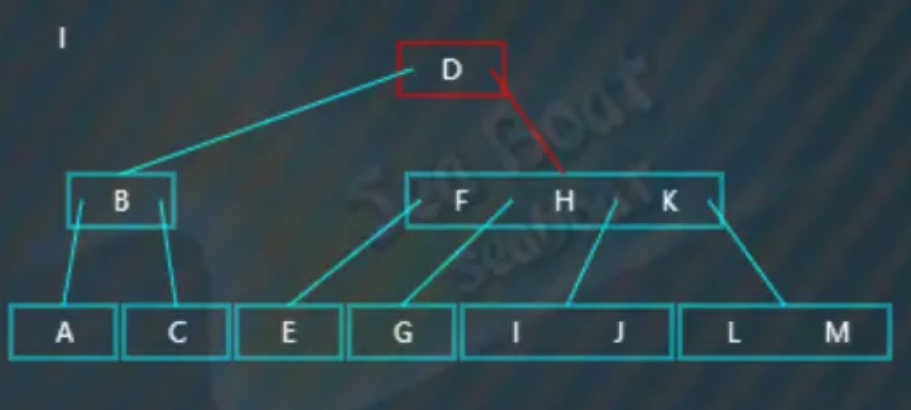
逐一与节点内的值进行比较,“I”大于“F”,继续比较,“I”大于“H”继续比较,“I”小于“K”,所以往第三个分支继续往下查找:
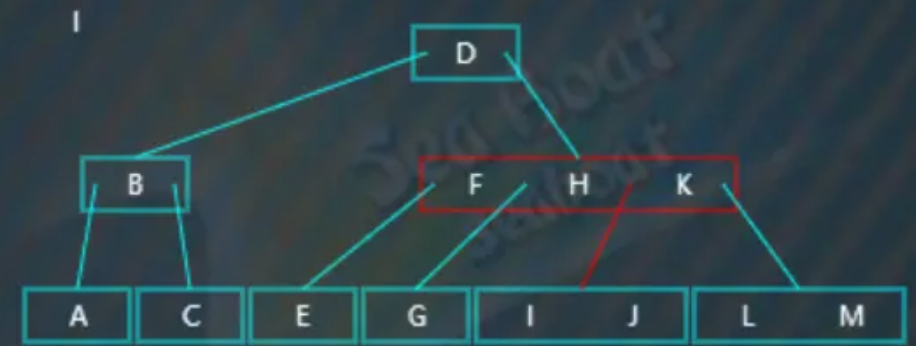
此时找到“I”:
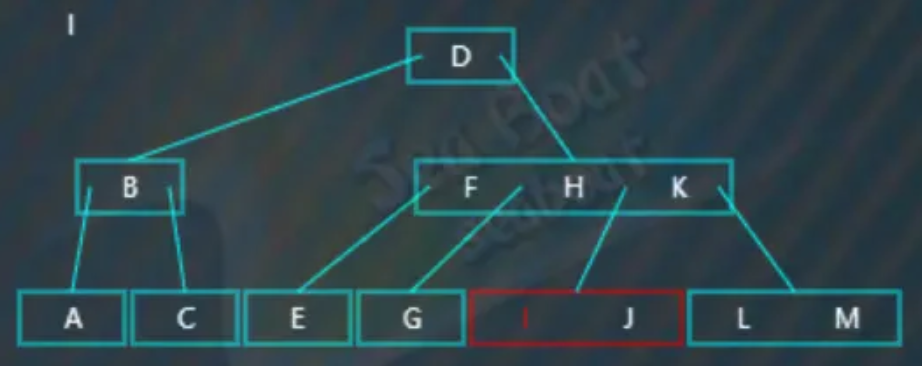
直接删除“I”,完成删除操作:
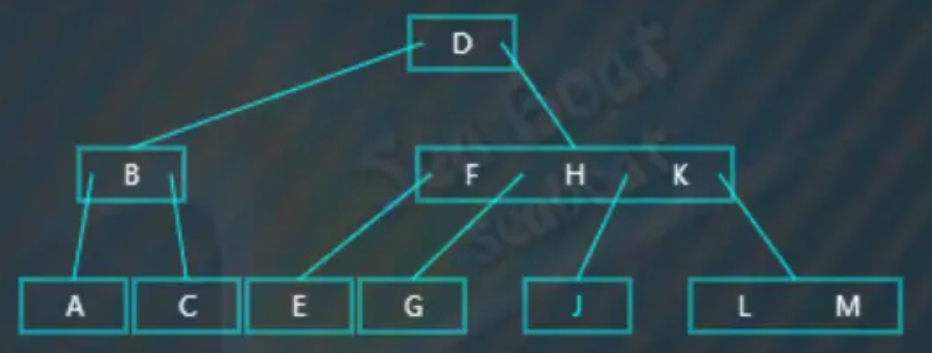
情况二 - 删除叶子节点,影响平衡,左旋
要删除的值在叶子节点上,而删除该值后,会打破B树的平衡,因此需要从右兄弟节点中借值,而且右兄弟节点中有足够的值借给它(或者说,这个右兄弟节点中包含大于等于两个值)。比如删除“G”,从根节点开始查找,“G”大于“D”,往右子树:
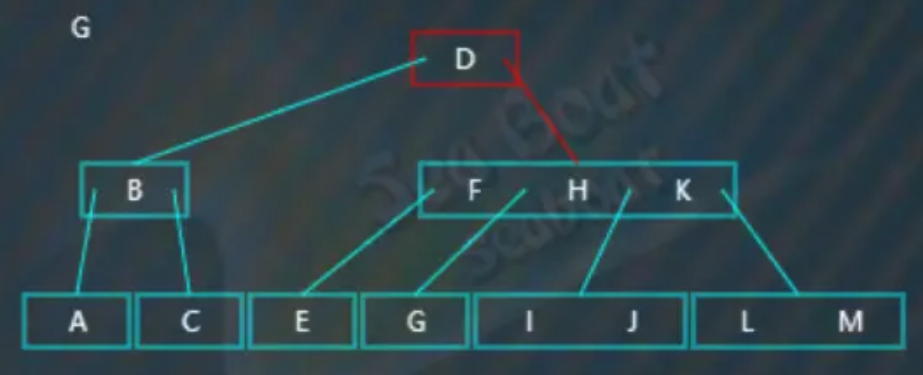
逐一比较节点内的值,发现应该往第二个分支:
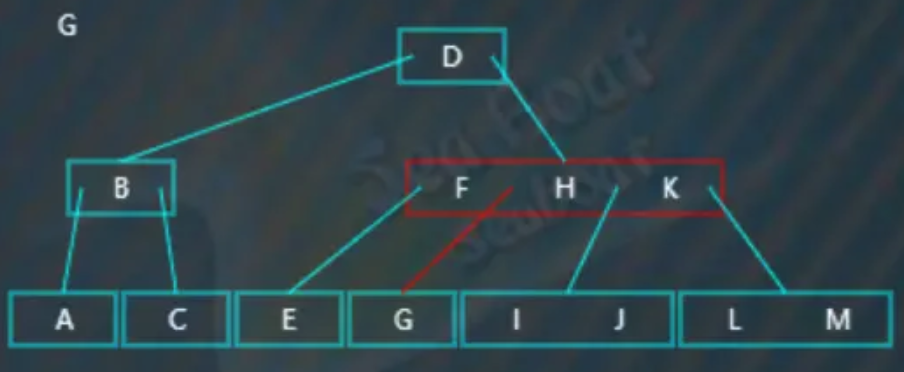
找到“G”:
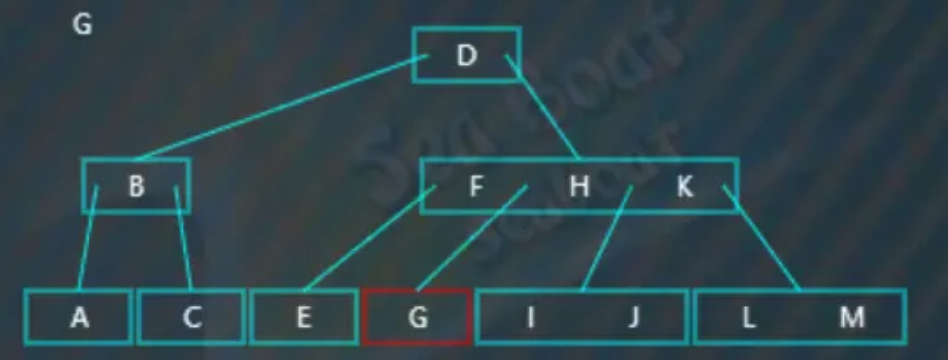
此时发现“G”节点的右兄弟节点有值可以借给它,于是删除“G”,然后进行左旋操作。左旋,即原来的父节点中的“H”值下移到左子节点中,以填补原来的“G”节点,右子节点中最小的值“I”提升到父节点,最终如下:
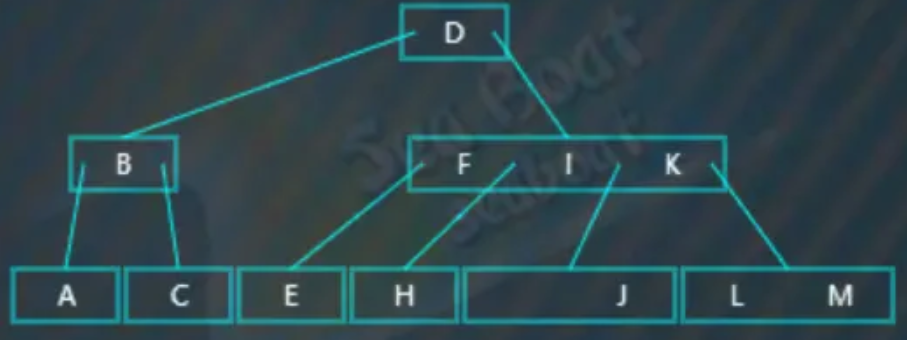
最终,完成删除操作:
情况三 - 删除叶子节点,影响平衡,右旋
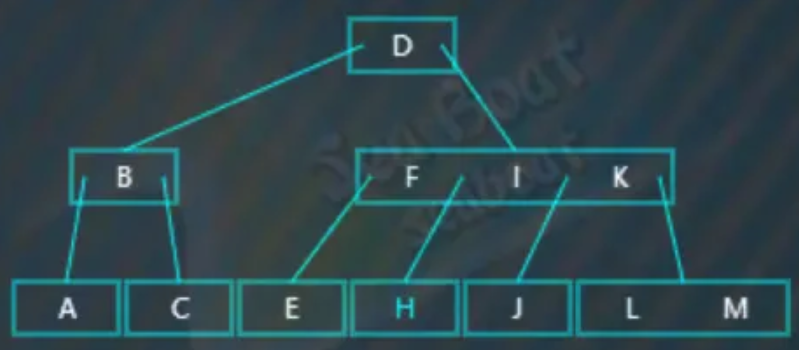
要删除的值在叶子节点上,删除该值,会打破B树的平衡,因此需要从左兄弟节点中借值,而且左兄弟节点有足够的值借给它(或者说,这个左兄弟节点中包含大于等于两个值)。比如删除“L”,从根节点开始查找,“L”大于“D”,往右子树:
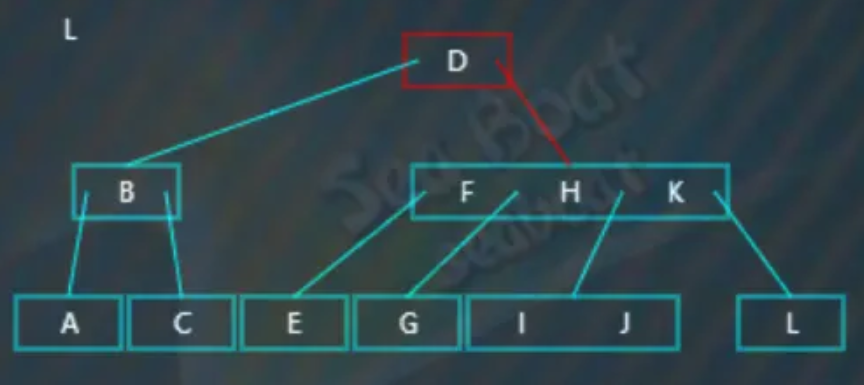
逐一比较节点内的值,发现应该往第四个分支:
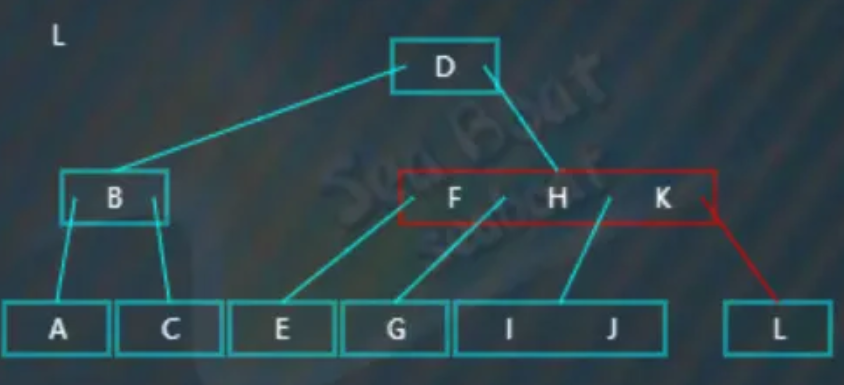
找到“L”:
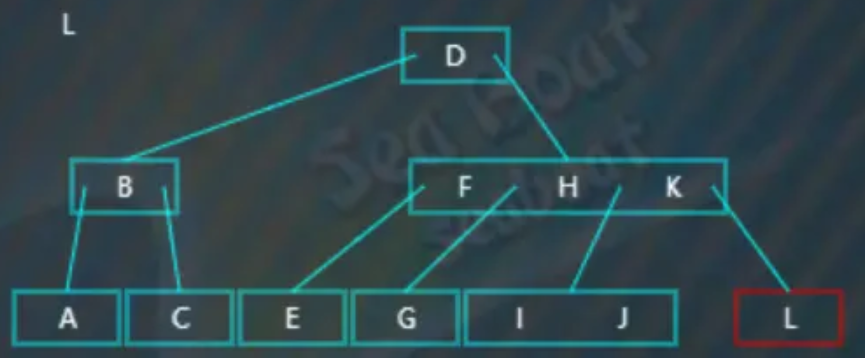
此时发现“L”节点的左兄弟节点有多的值可以借给它,于是删除“L”,然后进行右旋,右旋即原来的父节点中的“K”值下移到右子节点填补原来的“L”值,左子节点中最大的值“J”提升到父节点中,最终如下:
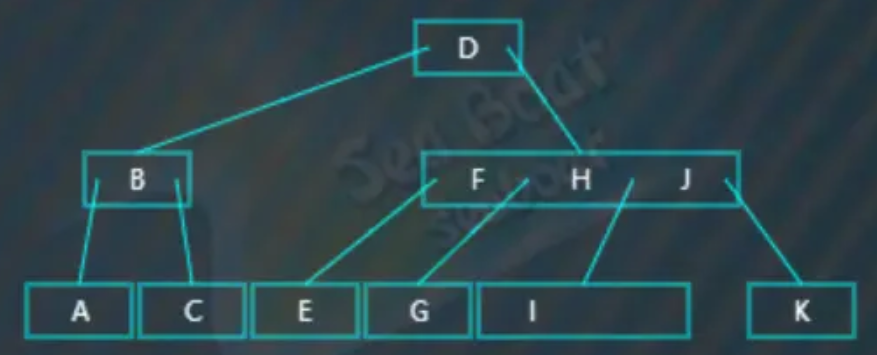
完成删除操作:
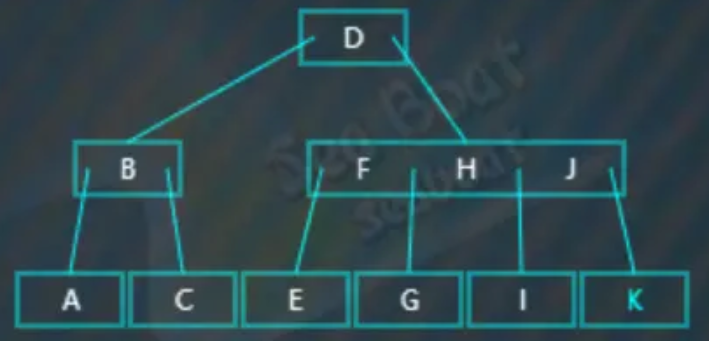
情况四 - 删除叶子节点,影响平衡
要删除的值在叶子节点上,删除后打破平衡,而且左右兄弟节点都没有值可以借给它(或者说,左右兄弟节点中分别只包含一个值)。比如删除“G”,从根节点开始查找,“G”大于“D”,往右子树:
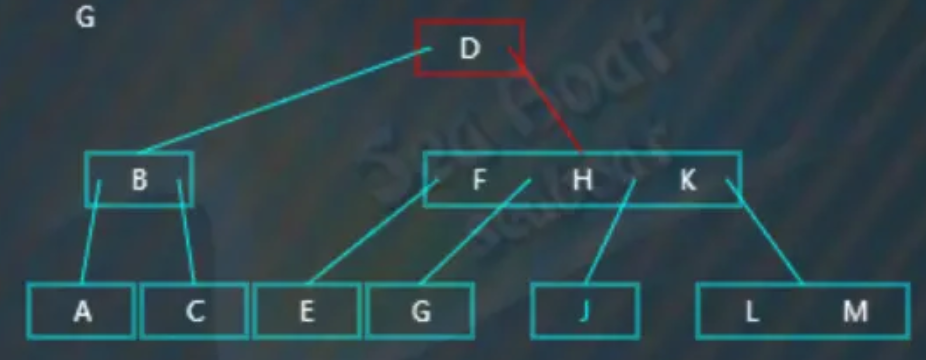
逐一比较节点内的值,发现应该往第二个分支:

找到“G”:
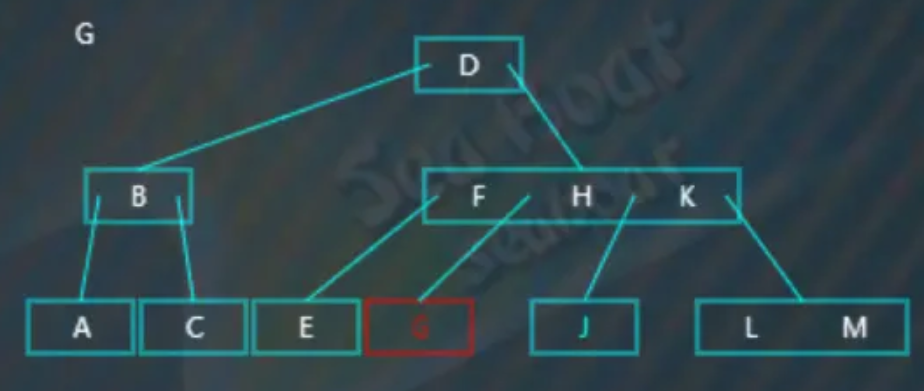
此时发现,“G”节点中的“G”值删除掉后,左右兄弟节点都无法借值给它,因此执行合并操作:
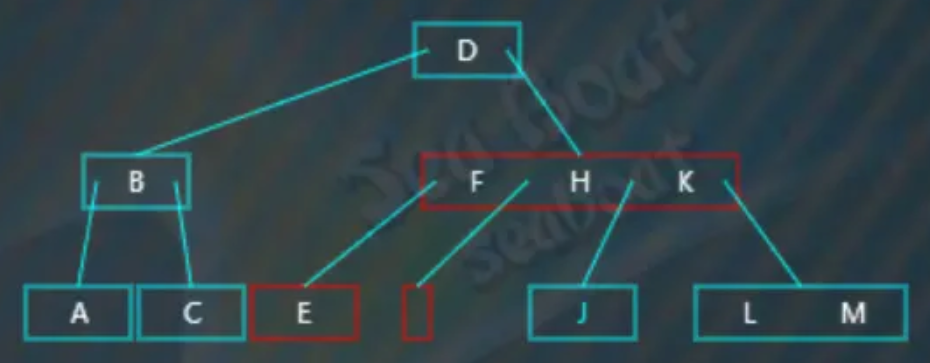
合并操作,是将父节点对应的“F”值下移到左子节点中,最终结果如下,完成删除操作:
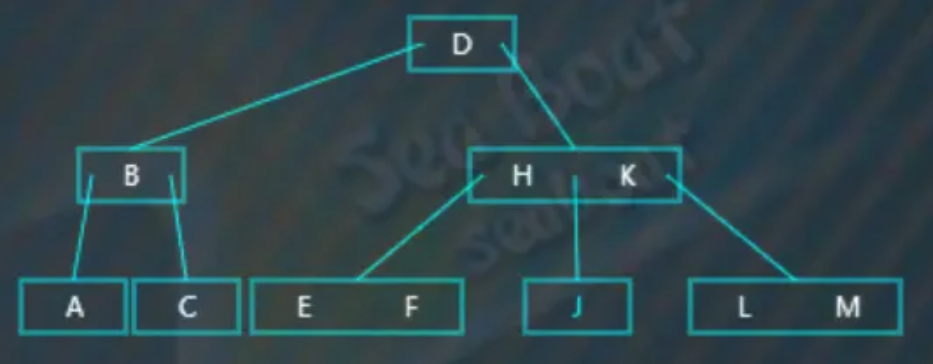
需要注意的是如果执行合并操作后使父节点不平衡,则需要继续对父节点继续进行平衡处理。比如下面的例子,需要删除“C”值,从根节点开始于“D”比较,小于“D”则往往第一个分支:
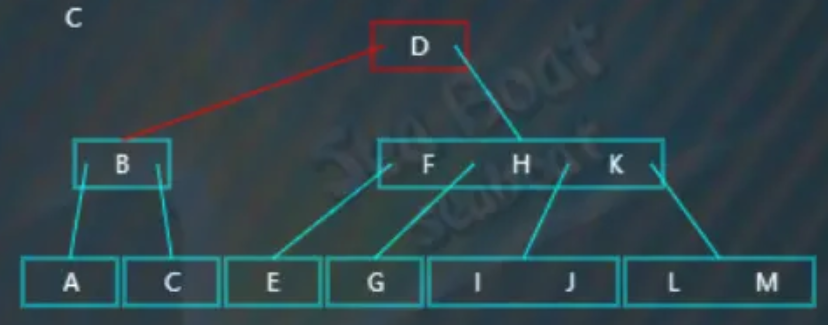
逐一与子节点内的值比较,“C”大于“B”则往第二个分支:
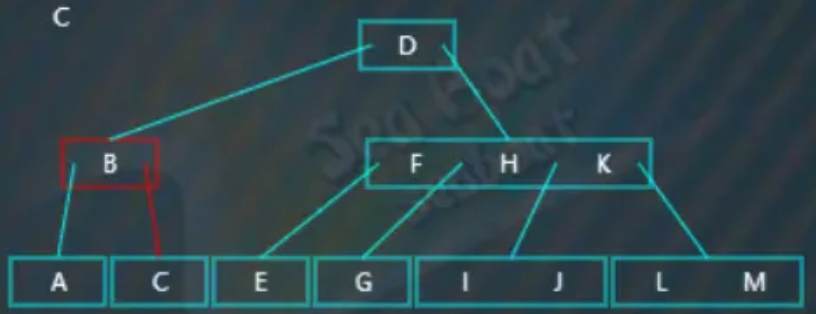
找到“C”:
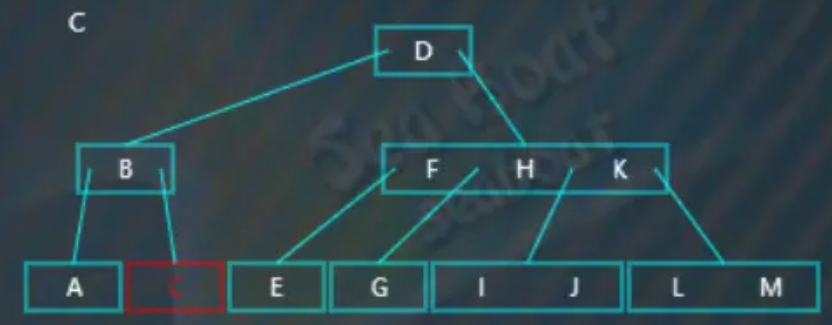
此时发现删除“C”值对应的节点后,左右兄弟节点都无法借值给它(因为左右兄弟节点都分别只包含一个值):
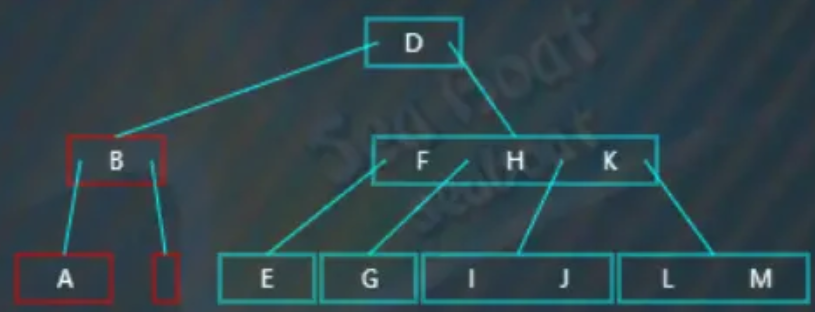
执行合并操作,将父节点中的值“B”下移到左子节点中,合并后结果如下,父节点已经变成空了,树不平衡:
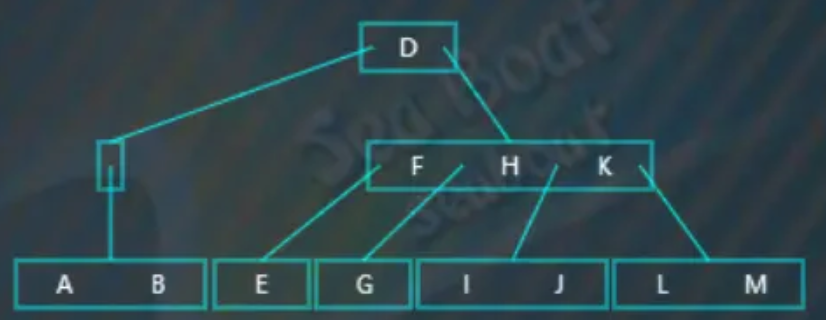
此时,父节点的右兄弟节点可以借值给它,即执行左旋操作,父节点的父节点的“D”值下移到父节点中,父节点的兄弟节点的最左边值“F”上移到父节点的父节点中:
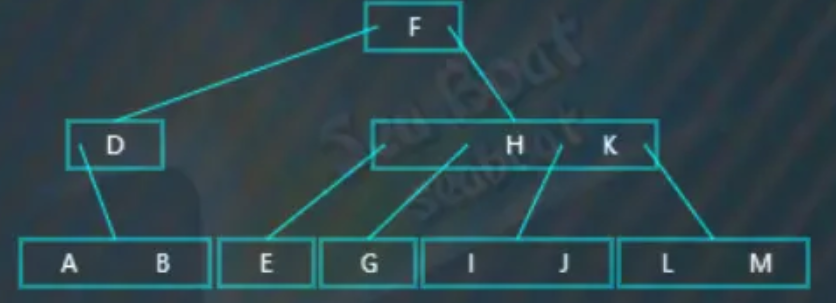
另外,左旋操作还包括要将移动值“F”对应节点的第一个分支(即“E”)移到父节点“D”的最右分支,最终结果如下:
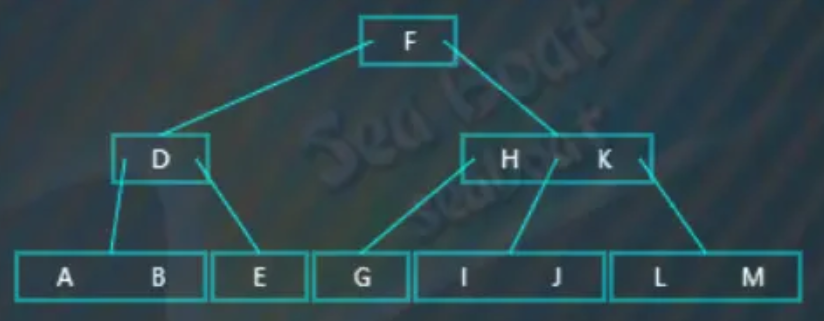
情况五 - 删除非叶子节点
要删除在非叶子节点上的值。比如删除“M”,从根节点开始查找,“M”大于“H”,往第二个分支:
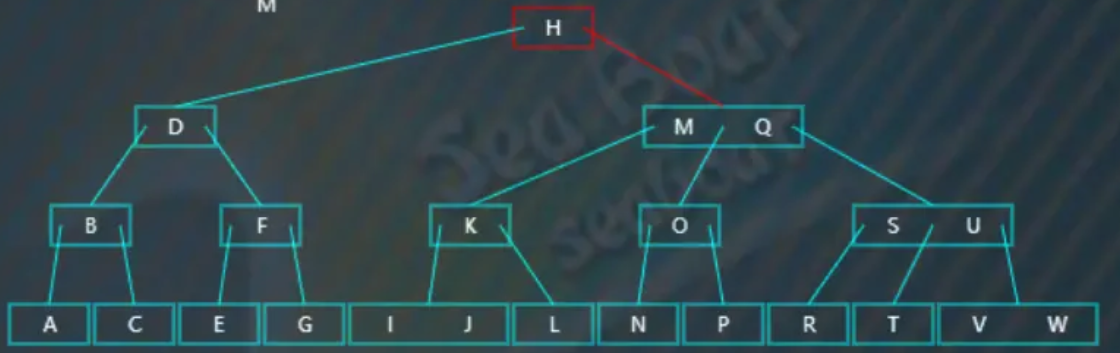
逐一比较子节点内的值,找到“M”,
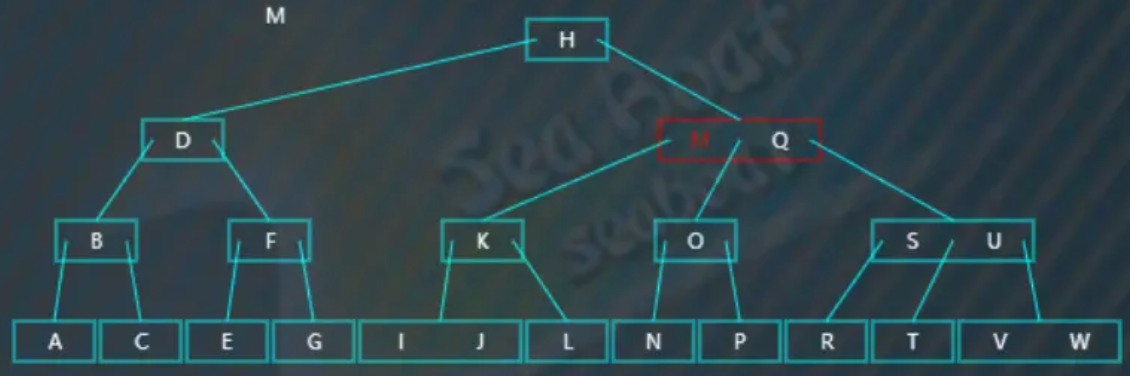
删除非叶子节点中值的第一步,就是要先找到对应的中序前驱,即第一个分支子节点中最大的值:
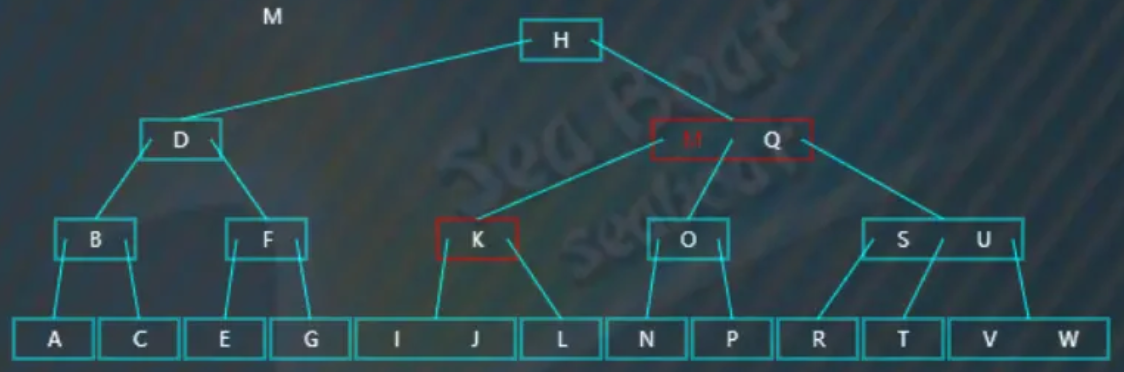
然后一直往最后一个分支找,最终找到“L”值为待删除值的中序前驱,将其提升到待删除值“M”的位置。提升后,导致了树不平衡,但它发现兄弟节点可以借值给它,
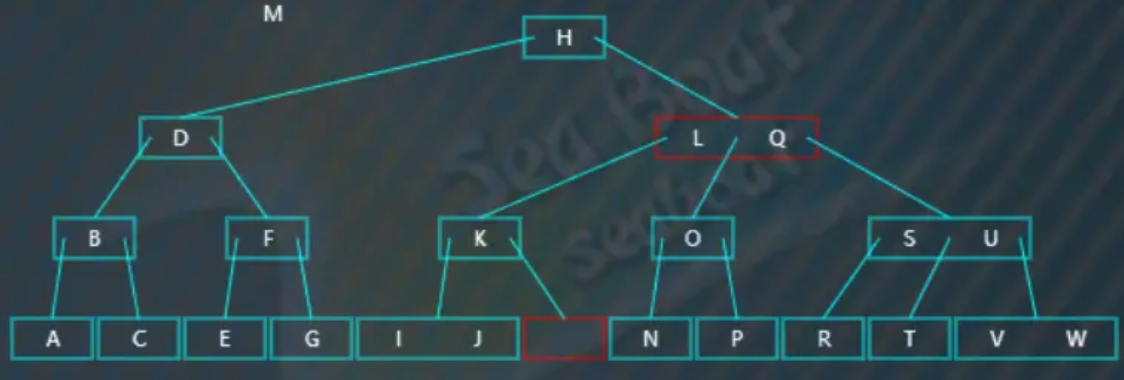
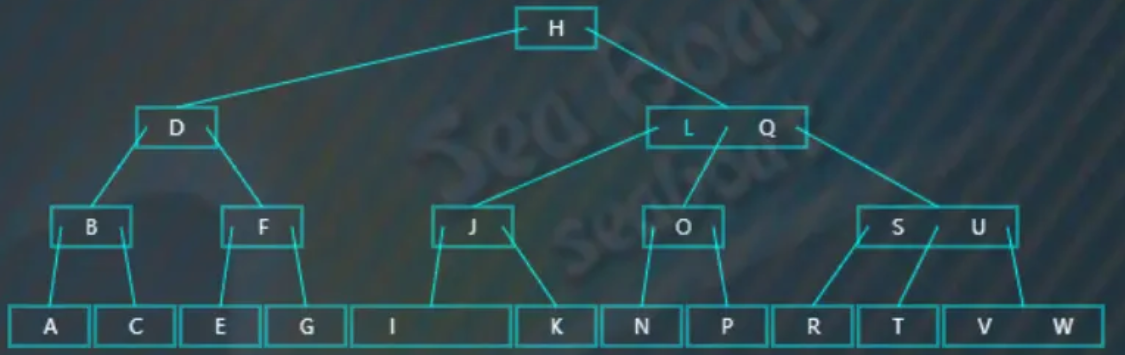
于是进行右旋操作,父节点中的“K”值下移到原来前驱节点的位置,左兄弟节点中最右边的值“J”提升到父节点中,另外如果左兄弟节点“J”值有右子节点的话,也需要挂到“K”节点的左边。最终完成删除操作。
除此之外,再看看删除根节点的情况,删除只有一个值的根节点,比如删除“D”,
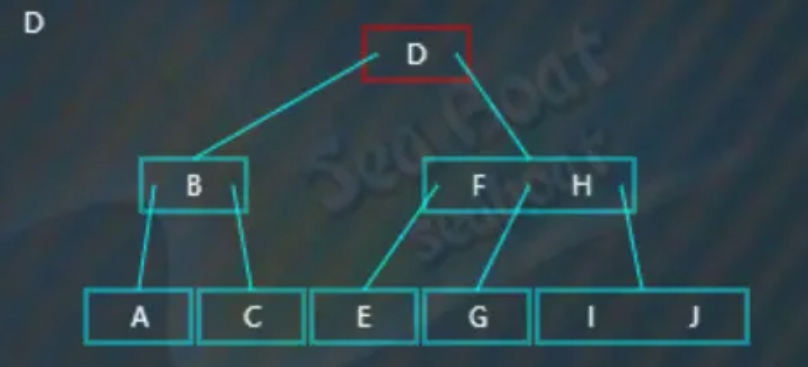
先找中序前驱,即第一个分支子节点中最大的值,
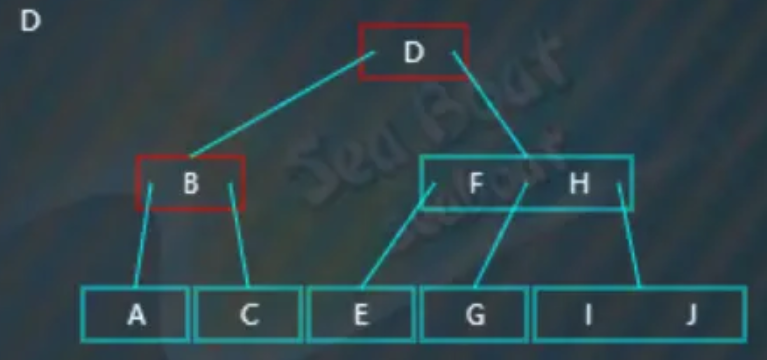
一直往最后一个分支找,最终找到“C”值为待删除值对应节点的前驱节点,将其提升到根节点中,
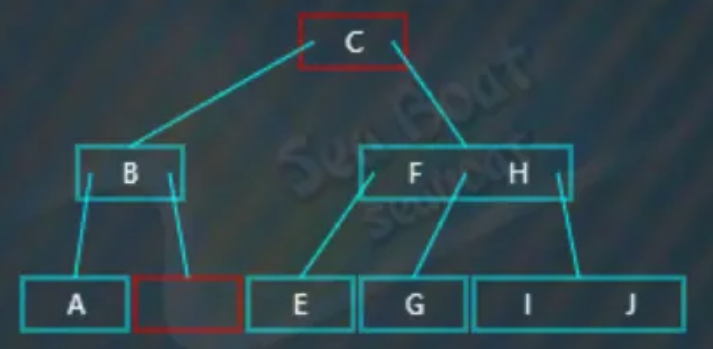
此时引起不平衡,而且原来“C”节点的左右兄弟节点都无法借值给它,
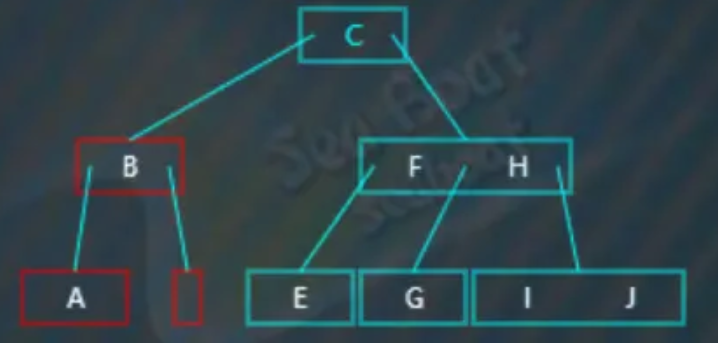
此时只能做合并处理,将父节点中的值“B”下移到左子节点,合并后原来的父节点变为空,产生了不平衡,此时它的兄弟节点可以借值给它,所以需要执行左旋操作:
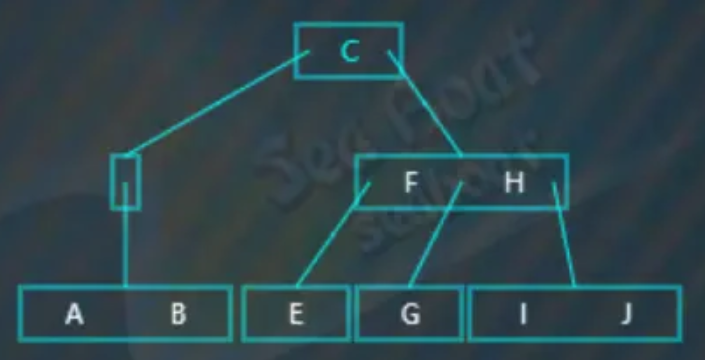
左旋即将“C”下移,“F”提升,
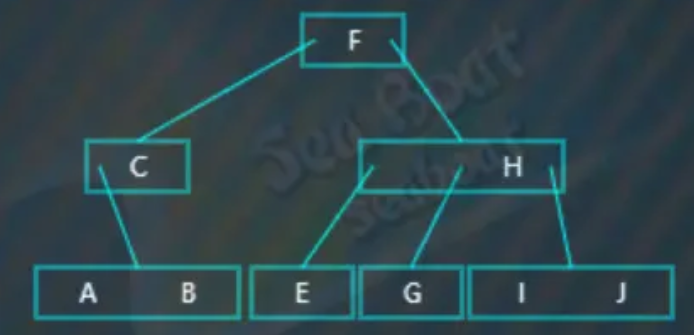
而且还要将“E”值挂到“C”节点上,最终如下。
Reference
- https://en.wikipedia.org/wiki/B-tree
- 看图轻松理解数据结构与算法系列(B树) - https://juejin.im/post/5b873a1af265da43741e2328
- 看图轻松理解数据结构与算法系列(B树的删除) - https://juejin.im/post/5b95ba52f265da0af87952a9
- MySQL索引背后的数据结构及算法原理 - http://blog.codinglabs.org/articles/theory-of-mysql-index.html