二叉树节点类
树节点
class TreeNode {
int val;
//左子树
TreeNode left;
//右子树
TreeNode right;
//构造方法
TreeNode(int x) {
val = x;
}
}
二叉树遍历(Traversal)
树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问,即依次对树中每个结点访问一次且仅访问一次,我们把这种对所有节点的访问称为遍历(traversal)。
那么树的两种重要的遍历模式是深度优先遍历(Depth-first Search,DFS)和广度优先遍历(Breadth-first Search,BFS) ,深度优先一般用递归,广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。
深度优先遍历(Depth-first Search,DFS)
对于一颗二叉树,** 深度优先搜索(Depth-first Search,DFS)** 是沿着树的深度遍历树的节点,尽可能深的查找树的分支。
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点,它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历(Pre-order Traversal),中序遍历(In-order Traversal)和后序遍历(Post-order Traversal)。
二叉树先序遍历(Pre-order Traversal)
二叉树先序遍历的实现思想是:
- 访问根节点;
- 访问当前节点的左子树;
- 若当前节点无左子树,则访问当前节点的右子树;
例子
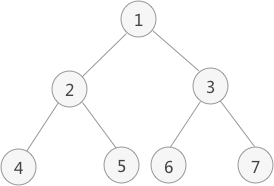
以上图为例,采用先序遍历的思想遍历该二叉树的过程为:
- 访问该二叉树的根节点,找到 1;
- 访问节点 1 的左子树,找到节点 2;
- 访问节点 2 的左子树,找到节点 4;
- 由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树,因此现在开始遍历,即访问节点 5;
- 由于节点 5 无左右子树,因此节点 5 遍历完成,并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ,并开始遍历该节点的右子树,即访问节点 3;
- 访问节点 3 左子树,找到节点 6;
- 由于节点 6 无左右子树,因此节点 6 遍历完成,回到节点 3 并遍历其右子树,找到节点 7;
- 节点 7 无左右子树,因此以节点 3 为根节点的子树遍历完成,同时回归节点 1。由于节点 1 的左右子树全部遍历完成,因此整个二叉树遍历完成;
因此,上图中二叉树采用先序遍历得到的序列为:
1 2 4 5 3 6 7
实现
递归(Recursive)实现
def preorder(root):
if not root:
return
print(root.val)
preorder(root.left)
preorder(root.right)
非递归(Iterative)实现
根据前序遍历的顺序,优先访问根结点,然后再访问左子树和右子树。
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
cur = root
while cur or stack:
if cur:
res.append(cur.val)
stack.append(cur.right)
cur = cur.left
else:
cur = stack.pop()
return res
二叉树中序遍历(In-order Traversal)
二叉树中序遍历的实现思想是:
- 访问当前节点的左子树;
- 访问根节点;
- 访问当前节点的右子树;
例子

以上图为例,采用中序遍历的思想遍历该二叉树的过程为:
- 访问该二叉树的根节点,找到 1;
- 遍历节点 1 的左子树,找到节点 2;
- 遍历节点 2 的左子树,找到节点 4;
- 由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树;
- 由于节点 4 无右子树,因此节点 2 的左子树遍历完成,访问节点 2;
- 遍历节点 2 的右子树,找到节点 5;
- 由于节点 5 无左子树,因此访问节点 5 ,又因为节点 5 没有右子树,因此节点 1 的左子树遍历完成,访问节点 1 ,并遍历节点 1 的右子树,找到节点 3;
- 遍历节点 3 的左子树,找到节点 6;
- 由于节点 6 无左子树,因此访问节点 6,又因为该节点无右子树,因此节点 3 的左子树遍历完成,开始访问节点 3 ,并遍历节点 3 的右子树,找到节点 7;
- 由于节点 7 无左子树,因此访问节点 7,又因为该节点无右子树,因此节点 1 的右子树遍历完成,即整棵树遍历完成;
因此,图 1 中二叉树采用中序遍历得到的序列为:
4 2 5 1 6 3 7
实现
递归(Recursive)实现
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def inorder(root):
if not root:
return
inorder(root.left)
res.append(root.val)
inorder(root.right)
return
inorder(root)
return res
非递归(Iterative)实现
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
cur = root
while stack or cur:
while cur:
stack.append(cur)
cur = cur.left
cur = stack.pop()
res.append(cur.val)
cur = cur.right
return res
二叉树后序遍历(Post-order Traversal)
二叉树后序遍历的实现思想是:从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素。
例子
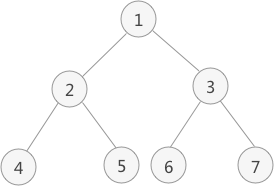
如上图中,对此二叉树进行后序遍历的操作过程为:
- 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点);
- 遍历节点 2 的左子树(以节点 4 为根节点);
- 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍历节点 2 的右子树(以 5 为根节点);
- 由于节点 5 无左右子树,因此可以访问节点 5 ,并且此时节点 2 的左右子树也遍历完成,因此也可以访问节点 2;
- 此时回退到节点 1 ,开始遍历节点 1 的右子树(以节点 3 为根节点);
- 遍历节点 3 的左子树(以节点 6 为根节点);
- 由于节点 6 无左右子树,因此访问节点 6,并回退到节点 3,开始遍历节点 3 的右子树(以节点 7 为根节点);
- 由于节点 7 无左右子树,因此访问节点 7,并且节点 3 的左右子树也遍历完成,可以访问节点 3;节点 1 的左右子树也遍历完成,可以访问节点 1;
- 到此,整棵树的遍历结束。
由此,对图 1 中二叉树进行后序遍历的结果为:
4 5 2 6 7 3 1
实现
递归(Recursive)实现
public void postOrderTraverse1(TreeNode root) {
if (root != null) {
postOrderTraverse1(root.left);
postOrderTraverse1(root.right);
System.out.print(root.val+" ");
}
}
非递归(Iterative)实现
public void postOrderTraverse2(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode pNode = root;
while (true){
while(pNode != null){
stack.push(pNode);
if(pNode.right != null)
stack.push(pNode.right);
pNode = pNode.left;
}
if(stack.isEmpty())
return;
pNode = stack.pop();
if( pNode.right != null && ! stack.isEmpty() && current.right == stack.peek() ) {
stack.pop();
stack.push(pNode);
pNode = pNode.right;
} else {
System.out.print( pNode.data + " " );
pNode = null;
}
}
}
广度优先遍历(Breadth-first Search,BFS)
二叉树层次遍历(Level-order Traversal)
前边介绍了二叉树的先序、中序和后序的遍历算法,运用了栈的数据结构,主要思想就是按照先左子树后右子树的顺序依次遍历树中各个结点。
本节介绍另外一种遍历方式:按照二叉树中的层次从左到右依次遍历每层中的结点。
具体的实现思路是:通过使用队列的数据结构,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。
例子
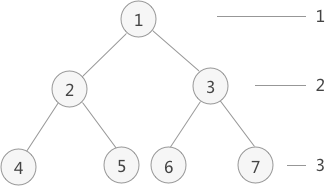
层次遍历上图中的二叉树:
- 首先,根结点 1 入队;
- 根结点 1 出队,出队的同时,将左孩子 2 和右孩子 3 分别入队;
- 队头结点 2 出队,出队的同时,将结点 2 的左孩子 4 和右孩子 5 依次入队;
- 队头结点 3 出队,出队的同时,将结点 3 的左孩子 6 和右孩子 7 依次入队;
- 不断地循环,直至队列内为空。
实现
非递归(Iterative)实现
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root:
return 0
level = 0
q = deque([root])
while q:
for i in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
level += 1
return level
Reference
- 二叉树的深度优先和广度优先遍历 - https://www.jianshu.com/p/473090b9490d