LFU(Least Frequently Used)
LFU (Least Frequently Used) 最近最不常用算法,它是根据频率维度来选择将要淘汰的元素,即删除访问频率最低的元素。如果两个元素的访问频率相同,则淘汰最久没被访问的元素。
也就是说LFU淘汰的时候会选择两个维度,先比较频率,选择访问频率最小的元素;如果频率相同,则按时间维度淘汰掉最久远的那个元素。
实现
LRU的实现是一个哈希表加上一个双链表,而LFU则要复杂多了,需要用两个哈希表再加上N个双链表才能实现,我们先看看LFU的两个哈希表里面都存了什么。
第一个哈希表是key-value的哈希表(以下简称kv哈希表)
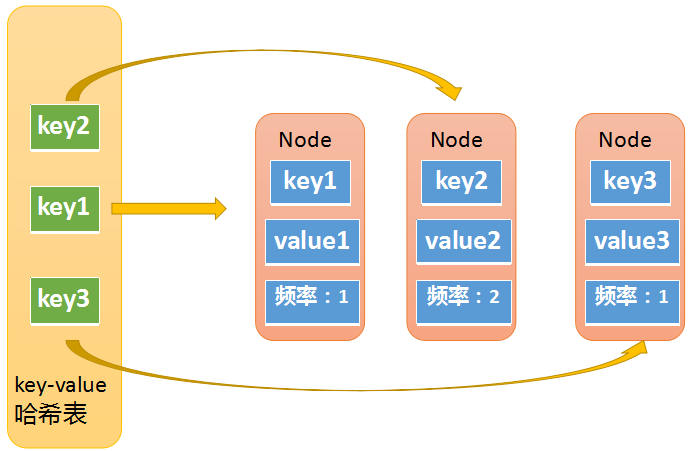
这里的key就是输入的key,没什么特别的。关键是value,它的value不是一个简单的value,而是一个节点对象。
节点对象Node包含了key,value,以及频率,这个Node又会出现在第二个哈希表的value中。
至于为什么Node中又重复包含了key,因为某些情况下我们不是通过k-v哈希表拿到Node的,而是通过其他方式获得了Node,之后需要用Node中的key去k-v哈希表中做一些操作,所以Node中包含了一些冗余信息。
第二张哈希表,频率哈希表,这个就要复杂多了
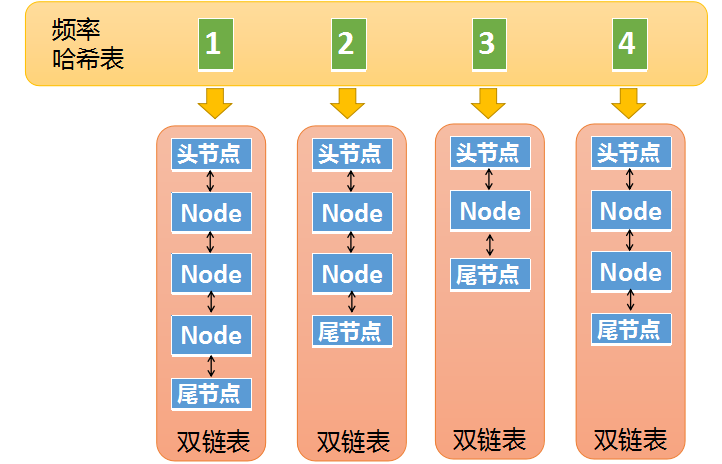
这张哈希表中的key是频率,也就是元素被访问的频率(被访问了1次,被访问了两次等等),它的value是一个双向链表。
刚才说的Node对象,现在又出现了,这里的Node其实是双向链表中的一个节点。
第一张图中我们介绍了Node中包含了一个冗余的key,其实它还包含了一个冗余的频率值,因为某些情况下,我们需要通过Node中的频率值,去频率哈希表中做查找,所以也需要一个冗余的频率值。
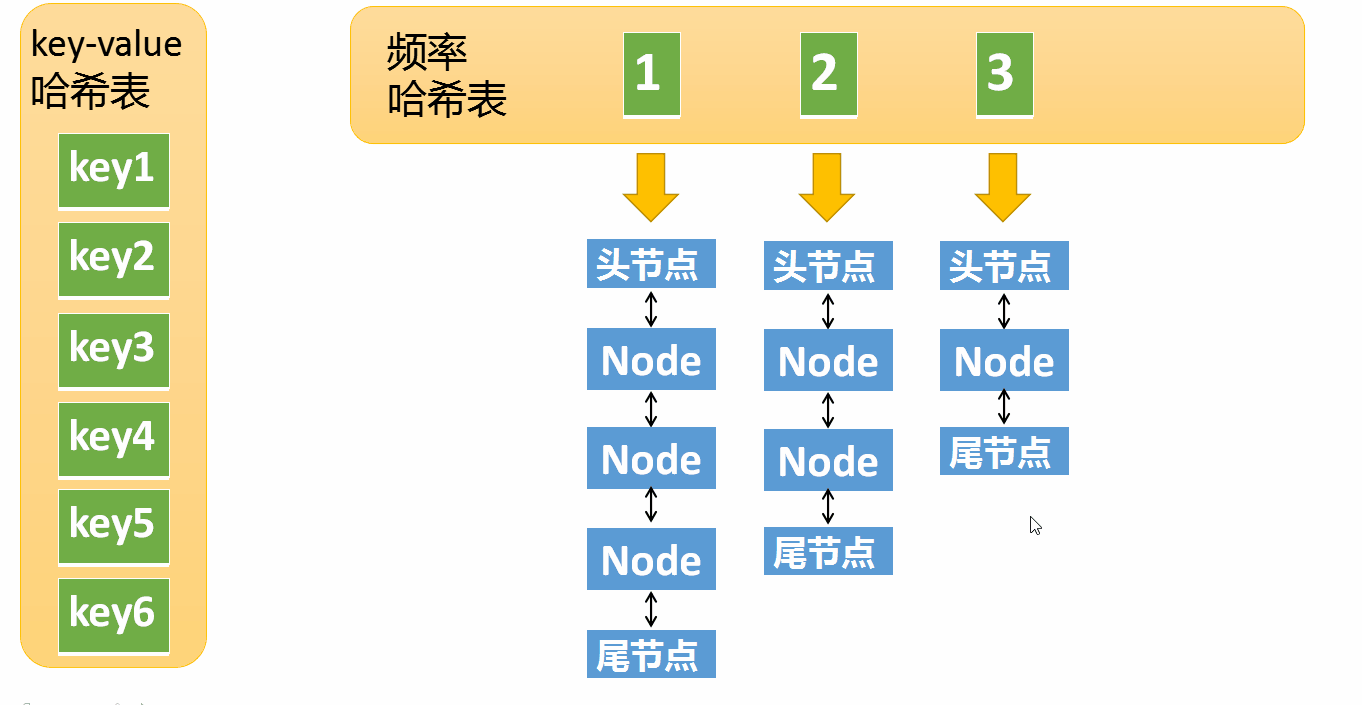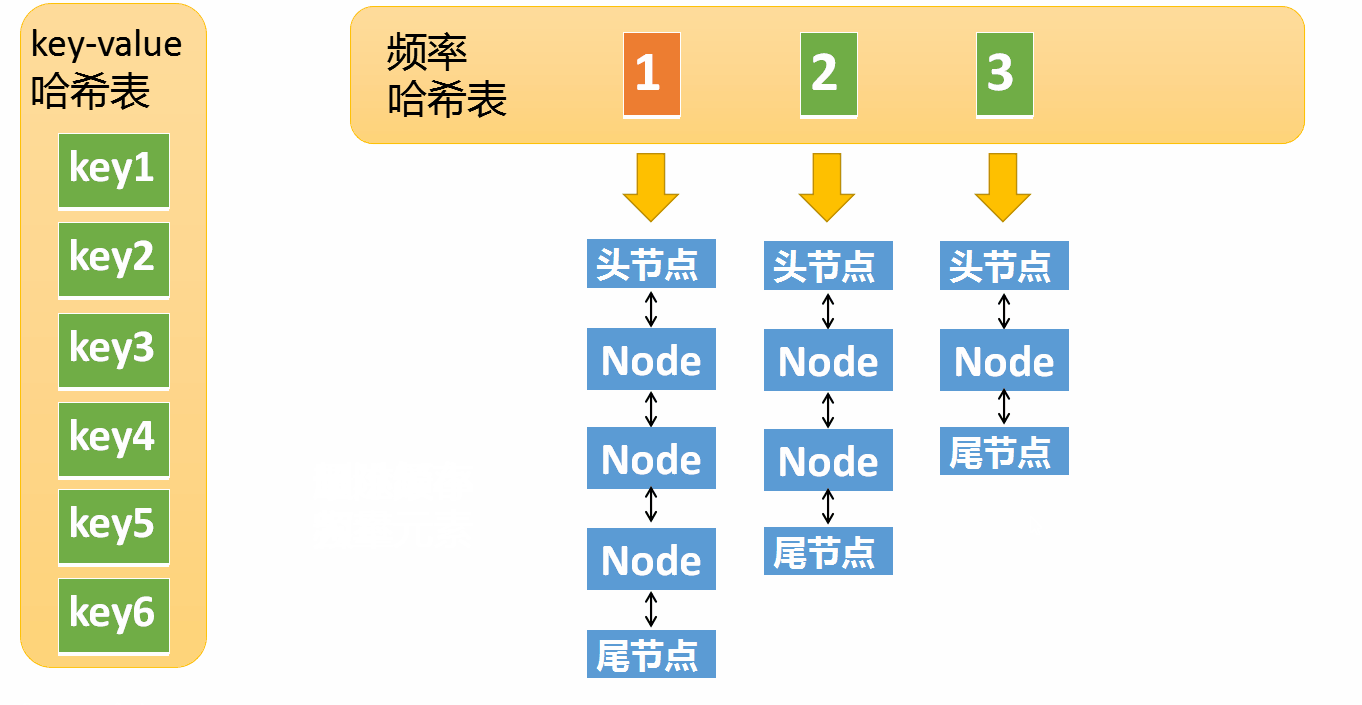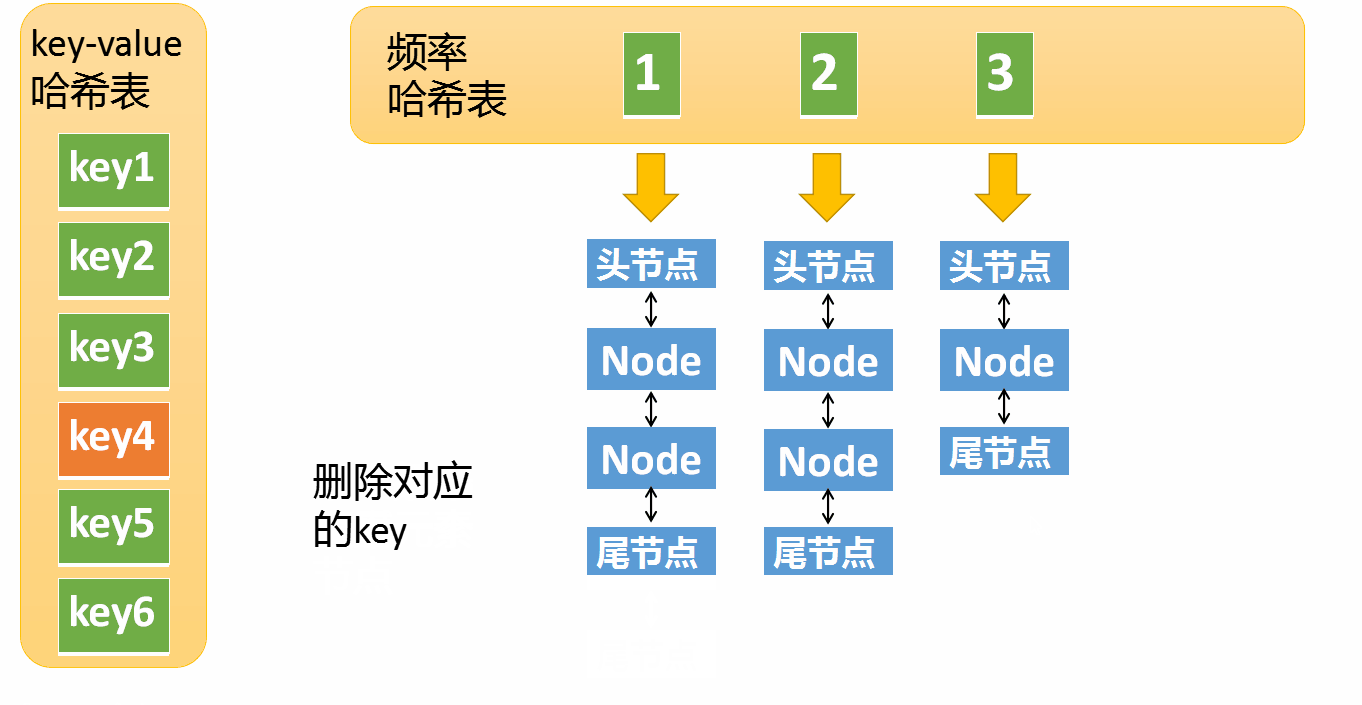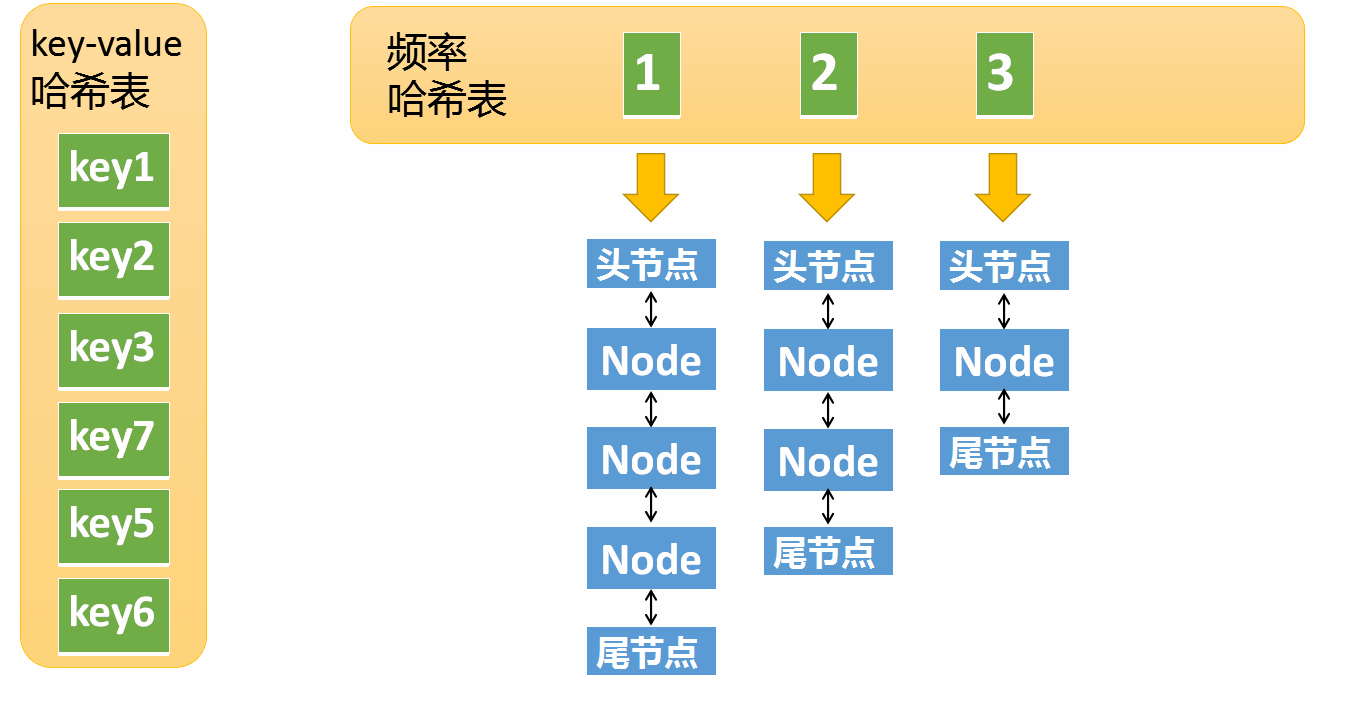
下面我们将两个哈希表整合起来看看完整的结构:
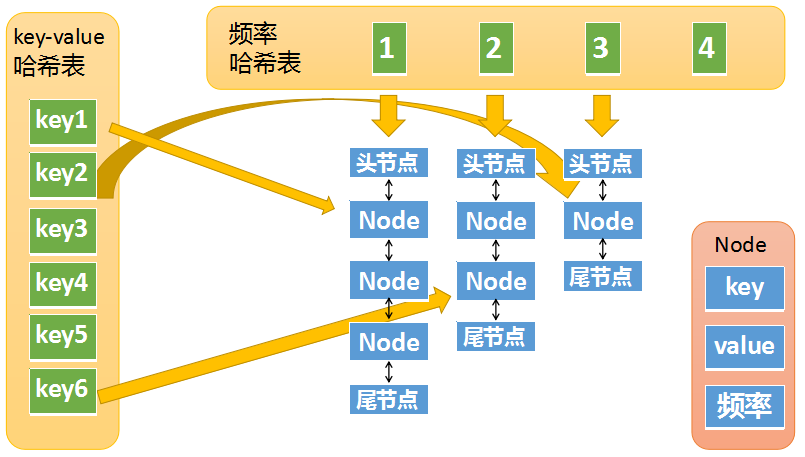
k-v哈希表中 key1 指向一个Node,这个Node的频率为1,位于频率哈希表中 key=1 下面的双链表中(处于第一个节点)。
具体操作
下面我们来看看具体操作,get操作相对简单一些,我们就先说get操作吧。
Get
get操作的具体逻辑大致是这样:
- 如果key不存在则返回-1
- 如果key存在,则返回对应的value,同时:
- 将元素的访问频率+1
- 将元素从访问频率i的链表中移除,放到频率+1的链表中
- 如果频率i的链表为空,则从频率哈希表中移除这个链表
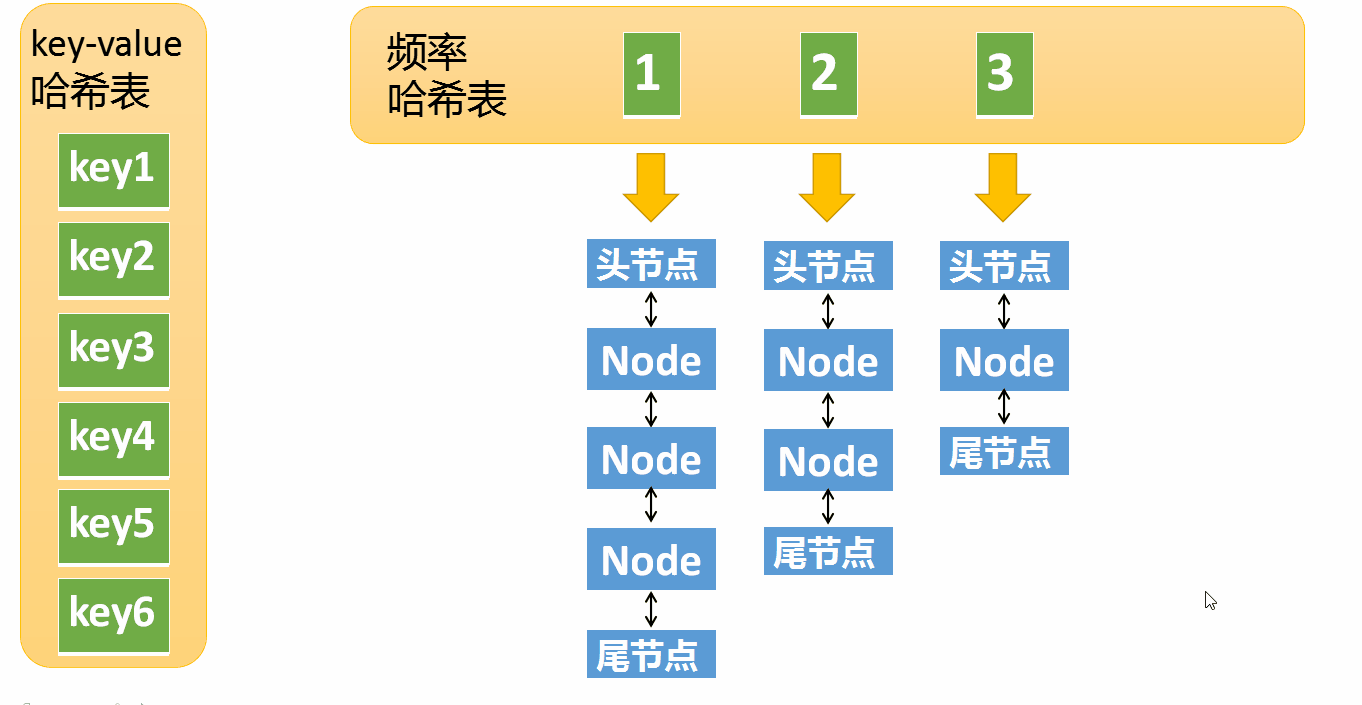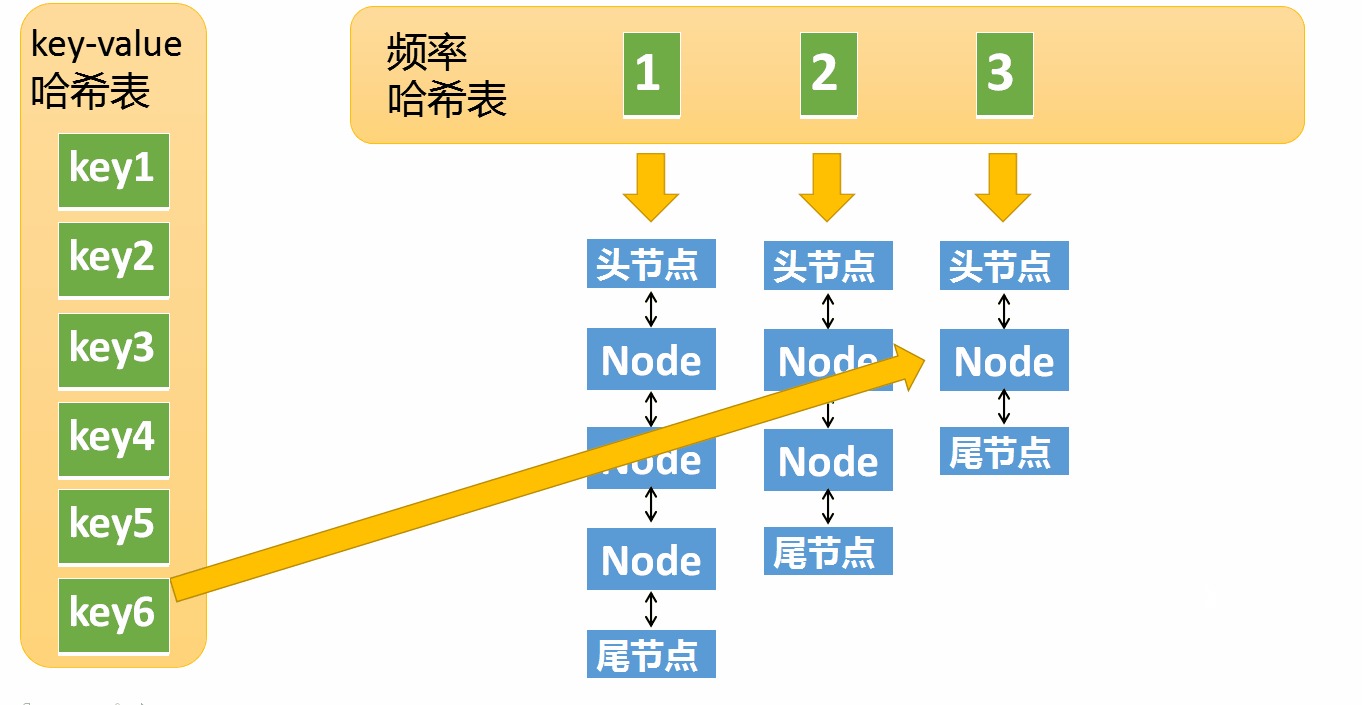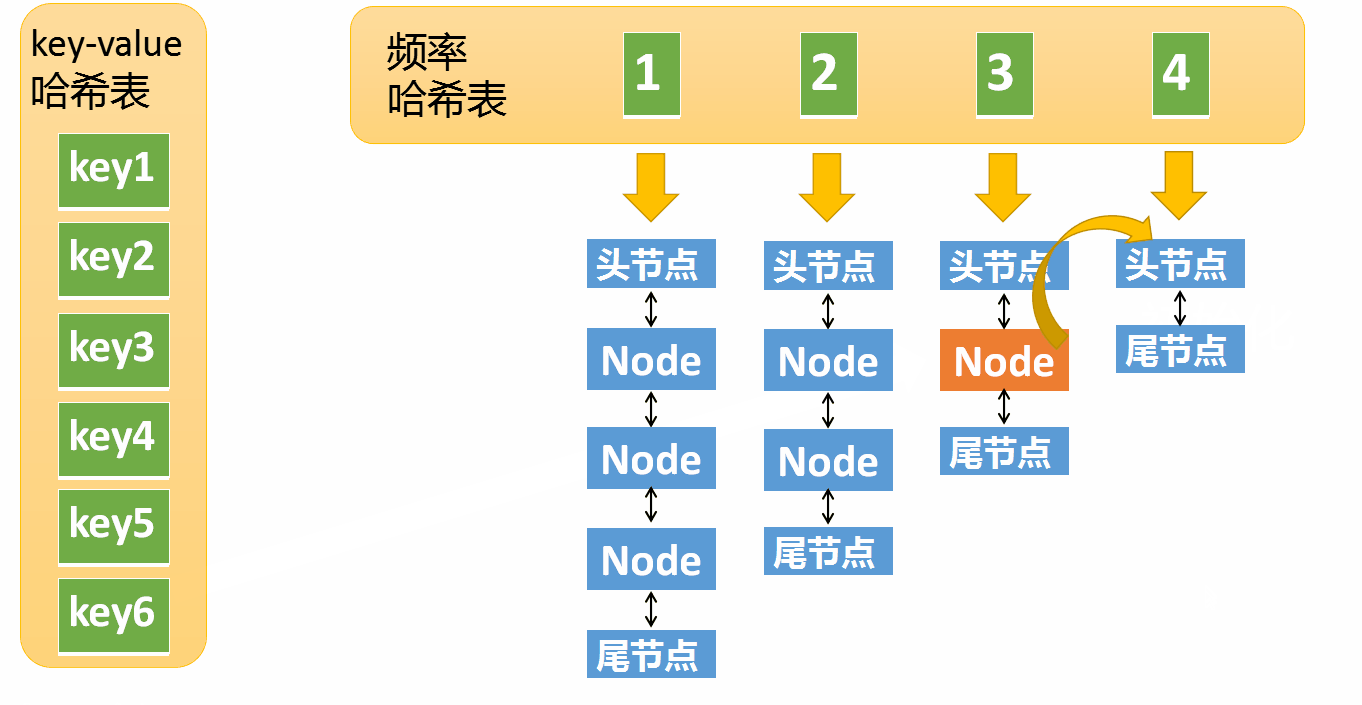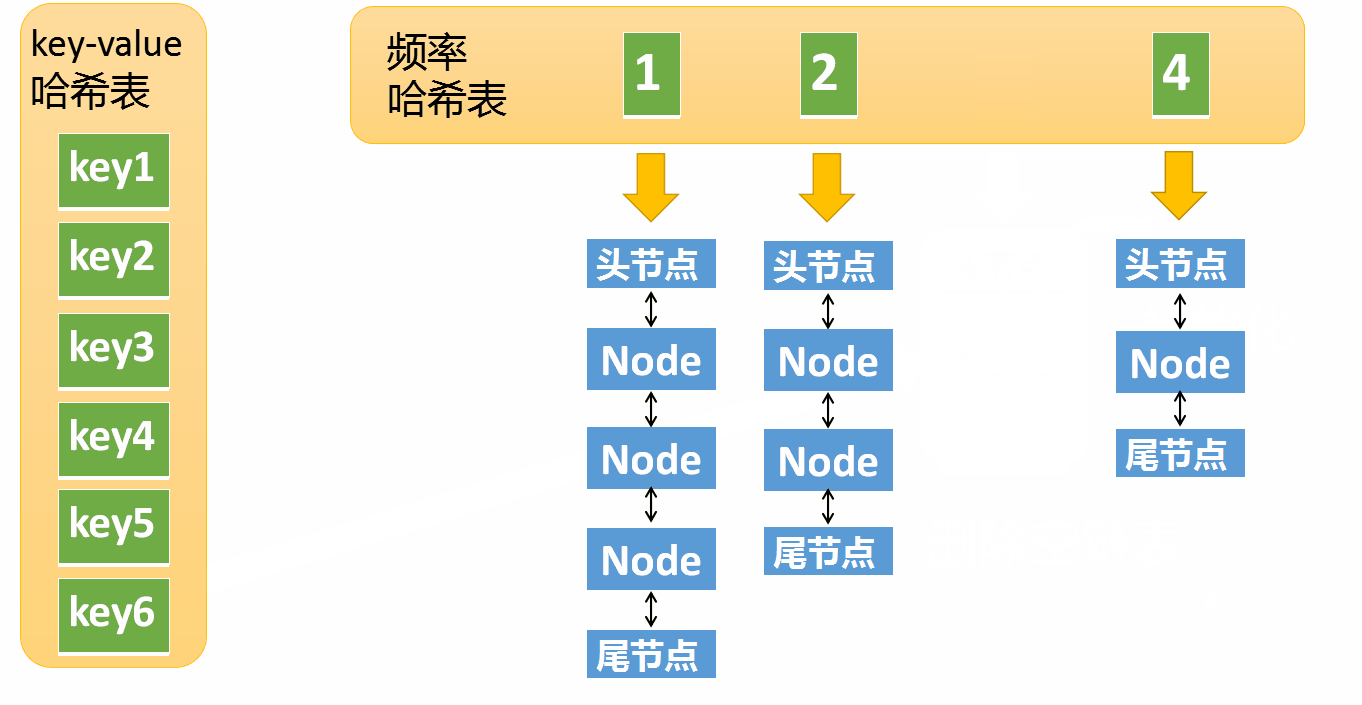
第一个很简单就不用说了,我们看下第二点的执行过程
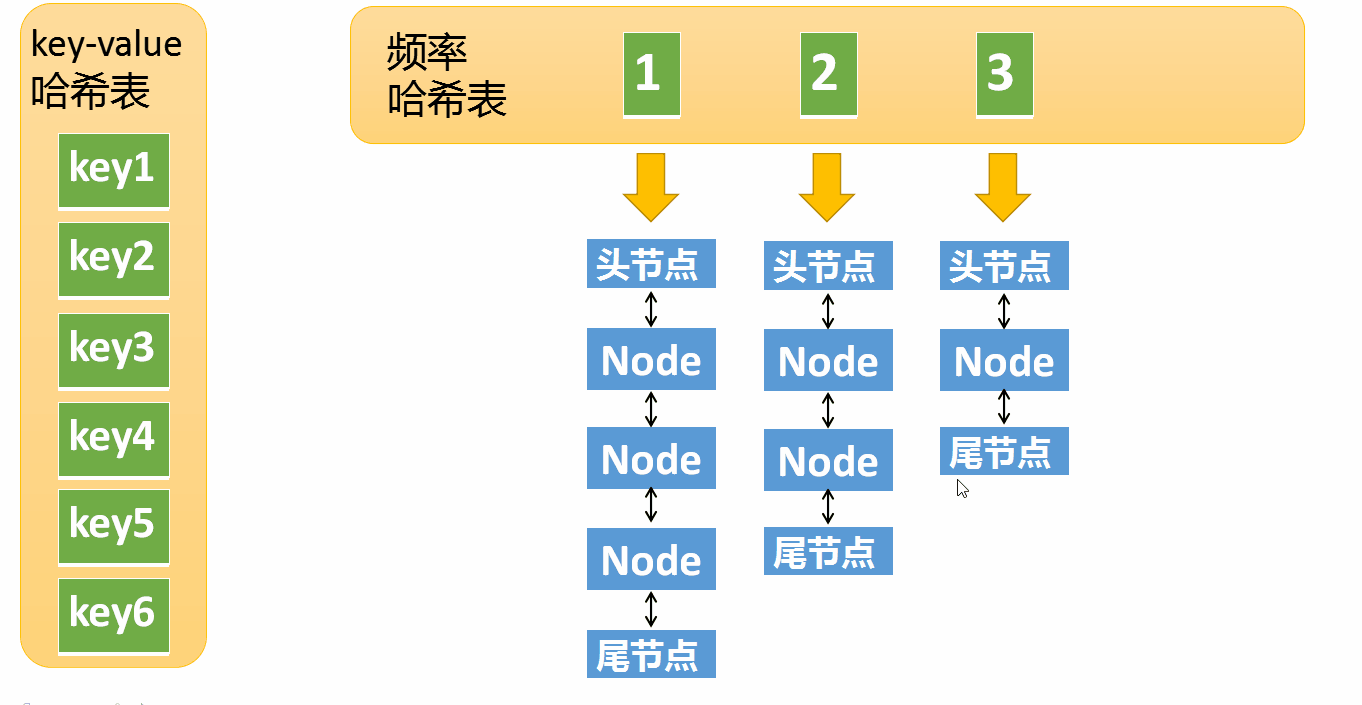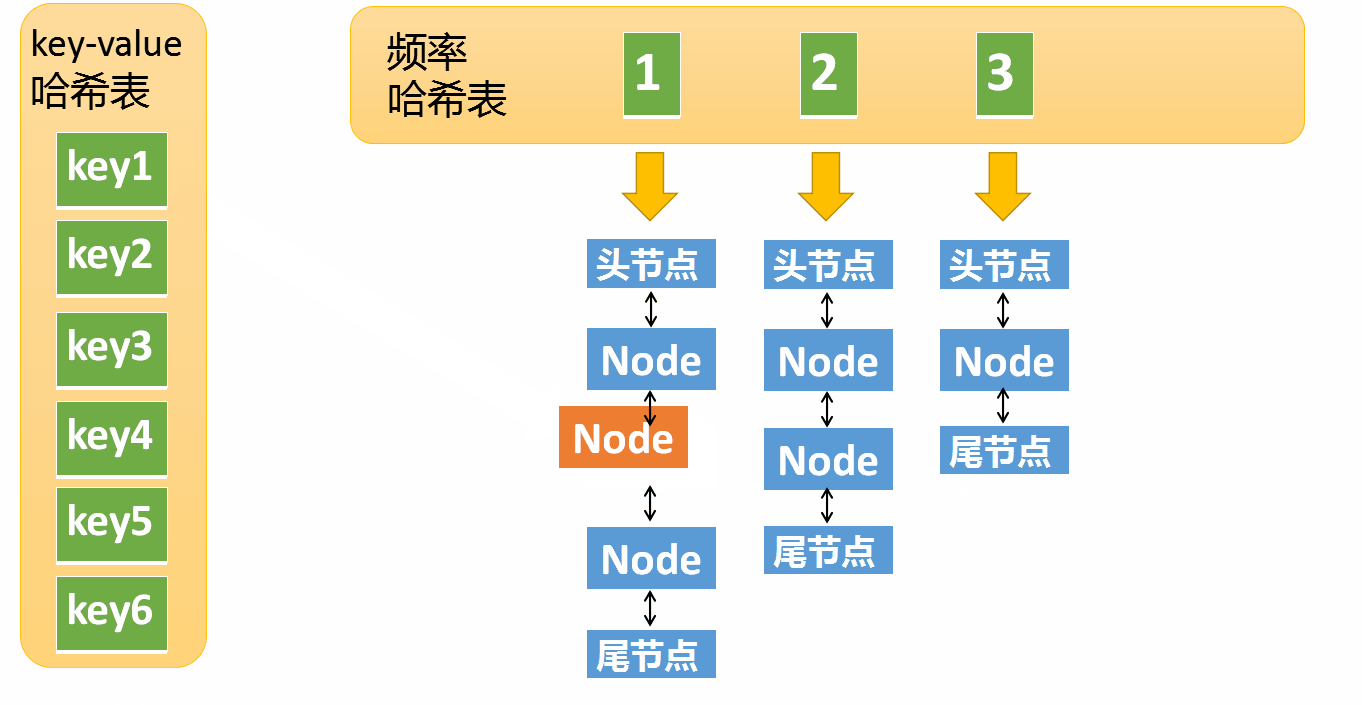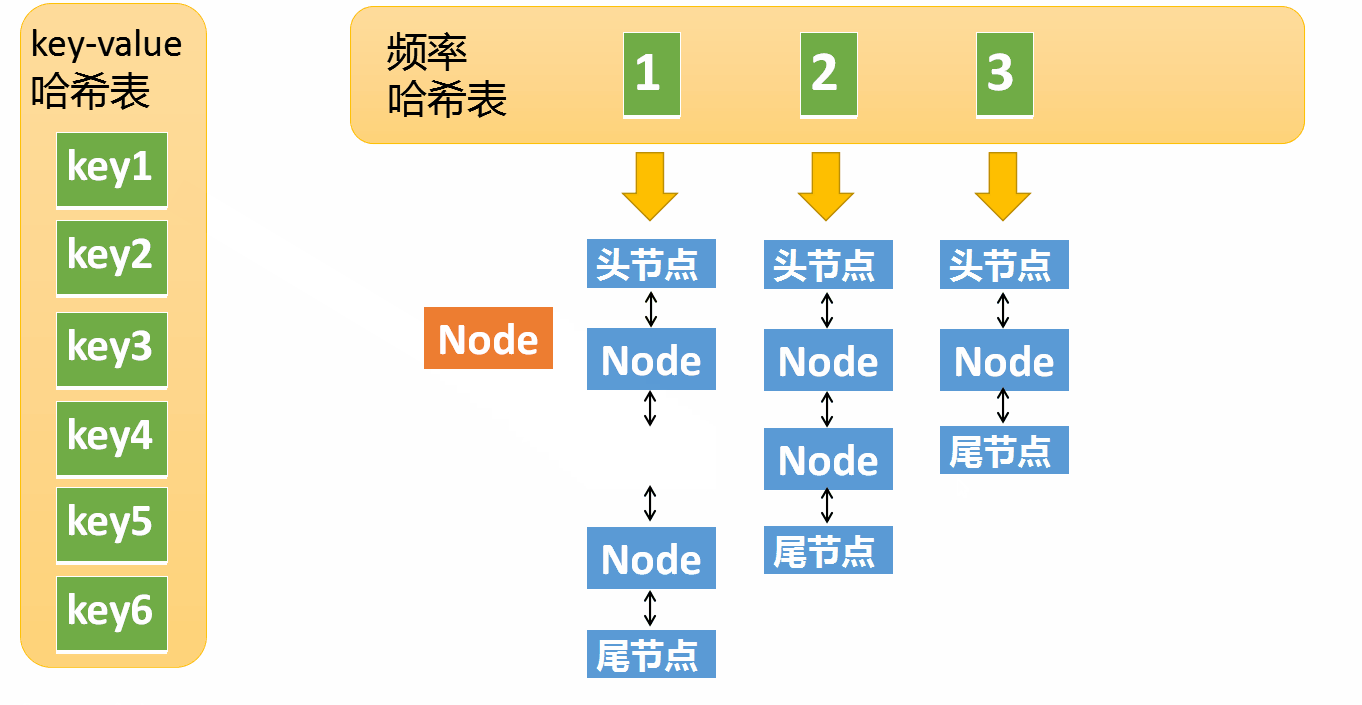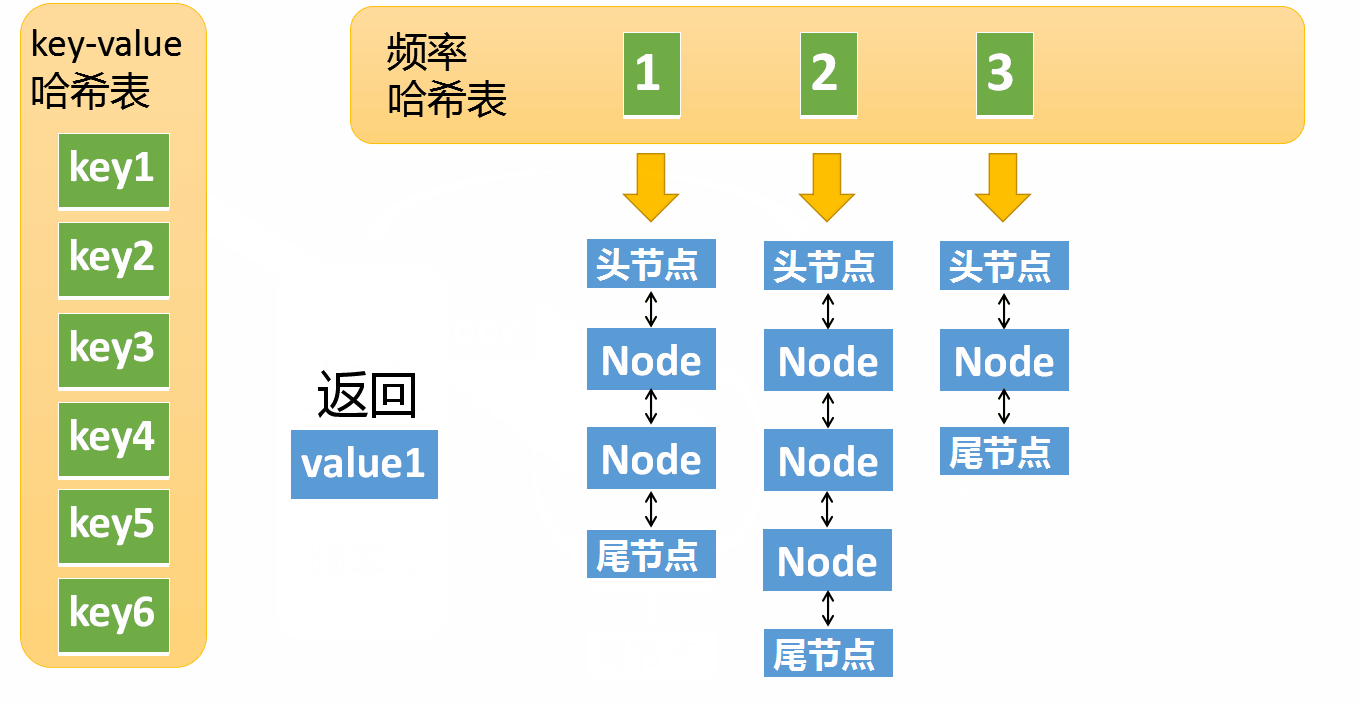
假设某个元素的访问频率是3,现在又被访问了一次,那么就需要将这个元素移动到频率4的链表中。如果这个元素被移除后,频率3的那个链表变成空了(即只剩下头结点和尾节点),就需要删除这个链表,同时删除对应的频率(也就是删除key=3)。
Put
put操作就要复杂多了,大致包括下面几种情况
- 如果key已经存在,修改对应的value,并将访问频率+1
- 将元素从访问频率i的链表中移除,放到频率+1的链表中
- 如果频率i的链表为空,则从频率哈希表中移除这个链表
- 如果key不存在
- 缓存超过最大容量,则先删除访问频率最低的元素,再插入新元素
- 新元素的访问频率为1,如果频率哈希表中不存在对应的链表,则需要创建
- 缓存没有超过最大容量,则插入新元素
- 新元素的访问频率为1,如果频率哈希表中不存在对应的链表,则需要创建
- 缓存超过最大容量,则先删除访问频率最低的元素,再插入新元素
我们在代码实现中还需要维护一个minFreq的变量,用来记录LFU缓存中频率最小的元素,在缓存满的时候,可以快速定位到最小频繁的链表,以达到 O(1) 时间复杂度删除一个元素。
具体做法是:
- 更新/查找的时候,将元素频率+1,之后如果minFreq不在频率哈希表中了,说明频率哈希表中已经没有元素了,那么minFreq需要+1,否则minFreq不变。
- 插入的时候,这个简单,因为新元素的频率都是1,所以只需要将minFreq改为1即可。
我们重点看下缓存超过最大容量时是怎么处理的