题目
10亿int整型数,以及一台可用内存为1GB的机器,时间复杂度要求O(n),统计只出现一次的数?
分析
首先分析多大的内存能够表示10亿的数呢?一个int型占4字节,10亿就是40亿字节(4 * 1000,000,000 Byte = 4GB),也就是如果完全读入内存需要占用4GB,而题目只给1GB内存,显然不可能将所有数据读入内存。
我们先不考虑时间复杂度,仅考虑解决问题。那么接下来的思路一般有两种。
- 位图法:用一个bit位来标识一个int整数。
- 分治法:分批处理这10亿的数。
一种是位图法,如果各位老司机有经验的话很快会想到int整型数是4字节(Byte),也就是32位(bit),如果能用一个bit位来标识一个int整数那么存储空间将大大减少。另一种是分治法,因为内存有限,因此我分批读取处理。下面大致分析一下两种思路。
位图法(Bitmap)
位图法是基于int型数的表示范围这个概念的,用两个bit位来标识一个int整数,若该位为01,则说明该数出现过一次;若为00,则说明该数没有出现,若为 11,则说明该数出现超过一次。一个int整型数占4字节(Byte),也就是32位(bit)。那么把所有int整型数字表示出来需要 $2 * 2^{32}$ bit的空间,换算成字节为单位也就是$2^{33}/8$ = $2^{30}$ Byte,大约等于1GB。
// 插播一个常识
2^10 Byte = 1024 Byte = 1KB
2^30 Byte = (2^10)^3 Byte = 1024 * 1024 * 1024 Byte = 1GB
这下就好办了,只需要用1GB的内存就能存储所有的int的范围数。
具体方案
那么接下来我们只需要申请一个int数组长度为 int tmp[N/32+1]即可存储完这些数据,其中N代表要进行查找的总数(这里也就是$2^{32}$),tmp中的每个元素在内存在占32位,所以可得到BitMap表:
- tmp[0]:可表示0~15
- tmp[1]:可表示16~31
- tmp[2]可表示32~47
- ~~
假设这10亿int数据为:6,3,8,16,18,……,那么具体的BitMap表示为:
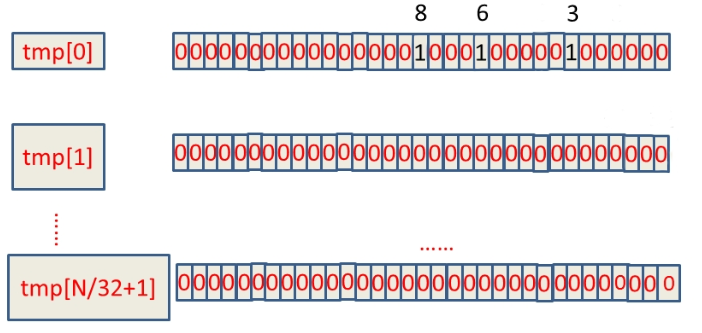
- 如何判断int数字放在哪一个tmp数组中:将数字直接除以16取整数部分(x/16),例如:整数15除以16取整等于0,那么15就在tmp[0]上;而整数 16 除以16取整等于1,那么 16 就在 tmp[1]上。
- 如何确定数字放在32个位中的哪个位(索引从 0 开始):将数字mod16取模再乘以 2(x % 16 * 2)。比如,我们知道了整数 0 在tmp[0]后,如果确定其在哪一位呢?计算0 % 16 * 2 = 0,因此在tmp[0]的第 0 位。又如整数8,8 % 16 * 2 = 16,因此在tmp[0]的第 16 位(从右边数起)。
- 然后,我们怎么统计只出现一次的数呢?每一个数出现的情况我们可以分为三种:0次、1次、大于1次。也就是说我们需要用2个bit位才能表示每个数的出现情况。此时则三种情况分别对应的bit位表示是:00、01、11。
我们顺序扫描这10亿的数,在对应的双bit位上标记该数出现的次数。最后取出所有双bit位为01的int型数就可以了。
Bitmap拓展
位图(Bitmap)算法思想比较简单,但关键是如何确定十进制的数映射到二进制bit位的map图。
优点:
- 运算效率高,不许进行比较和移位;
- 占用内存少,比如N=10000000;只需占用内存为N/8=1250000Byte=1.25M
**缺点:**所有的数据不能重复。即不可对重复的数据进行排序和查找。
适用场景
建立了Bit-Map之后,就可以方便的使用了。一般来说Bit-Map可作为数据的查找、去重、排序等操作。比如以下几个例子:
1 在3亿个整数中找出重复的整数个数,限制内存不足以容纳3亿个整数
对于这种场景可以采用2-BitMap来解决,即为每个整数分配2bit,用不同的0、1组合来标识特殊意思,如00表示此整数没有出现过,01表示出现一次,11表示出现过多次,就可以找出重复的整数了,其需要的内存空间是正常BitMap的2倍,为:3亿*2/8/1024/1024=71.5MB。
**具体的过程如下:**扫描着3亿个整数,组BitMap,先查看BitMap中的对应位置,如果00则变成01,是01则变成11,是11则保持不变,当将3亿个整数扫描完之后也就是说整个BitMap已经组装完毕。最后查看BitMap将对应位为11的整数输出即可。
2 对没有重复元素的整数进行排序
对于非重复的整数排序BitMap有着天然的优势,它只需要将给出的无重复整数扫描完毕,组装成为BitMap之后,那么直接遍历一遍Bit区域就可以达到排序效果了。
举个例子:对整数4、3、1、7、6进行排序:

直接按Bit位输出就可以得到排序结果了。
3 已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数
8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit==1.2MBytes,这样,就用了小小的1.2M左右的内存表示了所有的8位数的电话。
4 2.5亿个整数中找出不重复的整数的个数,内存空间不足以容纳这2.5亿个整数
将bit-map扩展一下,用2bit表示一个数即可:0表示未出现;1表示出现一次;2表示出现2次及以上,即重复,在遍历这些数的时候,如果对应位置的值是0,则将其置为1;如果是1,将其置为2;如果是2,则保持不变。或者我们不用2bit来进行表示,我们用两个bit-map即可模拟实现这个2bit-map,都是一样的道理。
最后放一个使用Byte[]数组存储、读取bit位的示例代码:
class BitmapTest {
private static final int CAPACITY = 1000000000;//数据容量
// 定义一个byte数组缓存所有的数据
private byte[] dataBytes = new byte[1 << 29];
public static void main(String[] args) {
BitmapTest ms = new BitmapTest();
byte[] bytes = null;
Random random = new Random();
for (int i = 0; i < CAPACITY; i++) {
int num = random.nextInt();
System.out.println("读取了第 " + (i + 1) + "\t个数: " + num);
bytes = ms.splitBigData(num);
}
System.out.println("");
ms.output(bytes);
}
/**
* 读取数据,并将对应数数据的 到对应的bit中,并返回byte数组
* @param num 读取的数据
* @return byte数组 dataBytes
*/
private byte[] splitBigData(int num) {
long bitIndex = num + (1l << 31); //获取num数据对应bit数组(虚拟)的索引
int index = (int) (bitIndex / 8); //bit数组(虚拟)在byte数组中的索引
int innerIndex = (int) (bitIndex % 8); //bitIndex 在byte[]数组索引index 中的具体位置
System.out.println("byte[" + index + "] 中的索引:" + innerIndex);
dataBytes[index] = (byte) (dataBytes[index] | (1 << innerIndex));
return dataBytes;
}
/**
* 输出数组中的数据
* @param bytes byte数组
*/
private void output(byte[] bytes) {
int count = 0;
for (int i = 0; i < bytes.length; i++) {
for (int j = 0; j < 8; j++) {
if (!(((bytes[i]) & (1 << j)) == 0)) {
count++;
int number = (int) ((((long) i * 8 + j) - (1l << 31)));
System.out.println("取出的第 " + count + "\t个数: " + number);
}
}
}
}
}
分治法
分治法目前看到的解决方案有哈希分桶(Hash Buckets)和归并排序两种方案。
哈希分桶的思想是先遍历一遍,按照hash分N桶(比如1000桶),映射到不同的文件中。这样平均每个文件就10MB,然后分别处理这1000个文件,找出没有重复的即可。一个相同的数字,绝对不会夸文件,有hash做保证。
Reference
- 【算法】10亿int型数,统计只出现一次的数 - https://itimetraveler.github.io/2017/07/13/%E3%80%90%E7%AE%97%E6%B3%95%E3%80%9110%E4%BA%BFint%E5%9E%8B%E6%95%B0%EF%BC%8C%E7%BB%9F%E8%AE%A1%E5%8F%AA%E5%87%BA%E7%8E%B0%E4%B8%80%E6%AC%A1%E7%9A%84%E6%95%B0/