AVL 树
在 1962 年,俄罗斯数学家 G. M. Andel’son-Vel-skii 和 E. M. Landis 发明了第一种自平衡二叉查找树,叫做 AVL 树。AVL 树必须维持如下平衡条件,对每个节点 n:节点 n 的左子树的高度与右子树的高度的差至多是 1。
节点的左子树或者右子树的高度可以通过上面描述的步骤来计算。如果节点仅有一个子节点,则无子节点侧的高度为 -1。
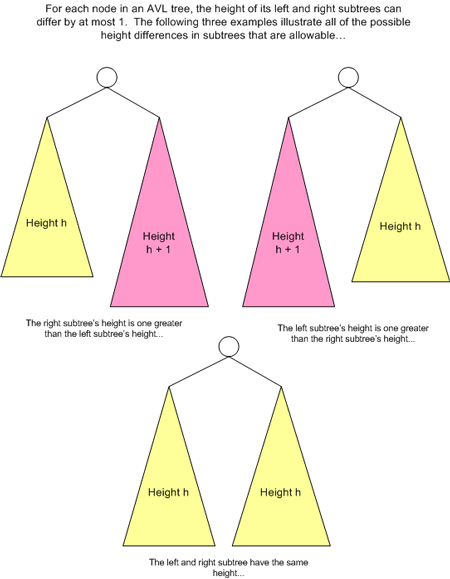
下图展示了概念上 AVL 树节点的两侧子树高度需要保持的关系。
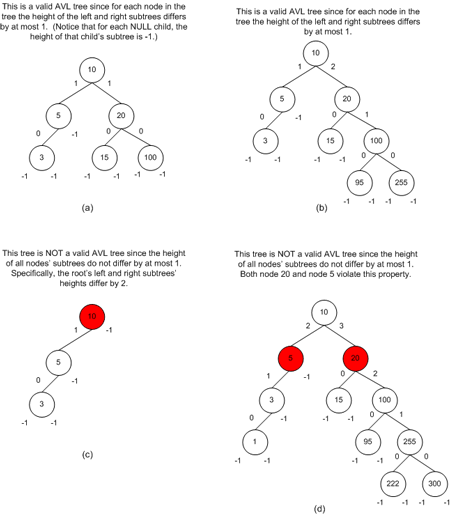
下面是一些二叉查找树。节点中的数字代表着节点的值,左右两侧的数字代表着左右子树的高度。其中树(a)和树(b)是合法的 AVL 树,而树(c)和树(d)则不合法,因为树中不是所有的节点都满足 AVL 的平衡性质要求。
AVL 树的平衡
当创建一棵 AVL 树时,难点在于如何保证 AVL 的平衡性质要求,而不用关注对树的具体操作。
也就是说,无论是向树添加节点还是删除节点,最重要的事情就是保持树的平衡。AVL 树通过 “旋转操作(rotations)” 来保持树的平衡。旋转操作可以重塑树的拓扑结构来恢复树的平衡,更重要的是,重塑后的树依然符合二叉查找树的性质要求。
当向一棵 AVL 树中插入一个新的节点时,需要经过两阶段的过程。首先,插入新节点的操作将使用与向 BST 树中插入新节点时使用的相同的查找算法。新的节点将做为一个叶子节点被添加到树中合适的位置,以满足 BST 的性质要求。在添加完节点后,将导致树的结构可能已经违背 AVL 树的性质要求。所以在第二个阶段中,将遍历访问路径,来检查每个节点左右子树高度。如果存在某节点的左右子树的高度差大于 1 时,则需要使用旋转操作来处理。
平衡二叉树的修正机制
当我们计算出某个结点的平衡因子的绝对值超过1时, 我们就要对其进行修正, 即通过平衡化的处理,使得不平衡的二叉树重新变得平衡。
平衡化操作的四种情况
AVL在构造的时候失衡以及平衡处理的方式包括以下四种:
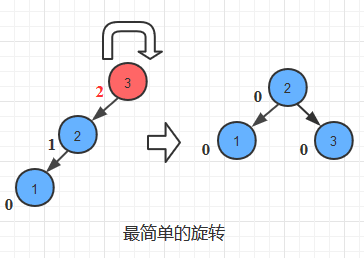
LL失衡 - 右旋(Zig)
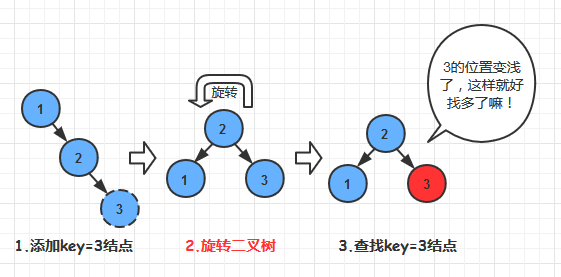
RR失衡 - 左旋(Zag)
LR失衡 - 先左旋后右旋(Zig-zag)
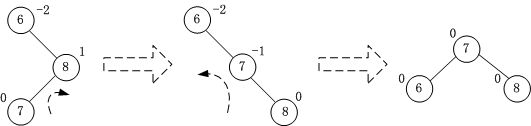
RL失衡 - 先右旋后左旋(Zag-zig)
第四种情况与第三种情况类似,为RL失衡,处理方式是先右旋后左旋(Zag-zig)。
平衡动图

这里我们可以很明显地看到平衡二叉树的优势所在: 使得查找的平均深度降低, 优化各个API的性能开销。
平衡二叉树和普通二叉查找树区别主要在于动态方法(put,delete) ,而它们的静态方法(get,min,max,floor,ceiling, rank,select)基本是相同的。
Reference
- 自平衡二叉查找树 - https://www.cnblogs.com/gaochundong/p/self_balancing_binary_search_tree.html
- 一篇搞懂AVL平衡二叉树 - https://zhuanlan.zhihu.com/p/34840762、
- 【算法】论平衡二叉树(AVL)的正确种植方法 - https://www.cnblogs.com/penghuwan/p/8166133.html