背景
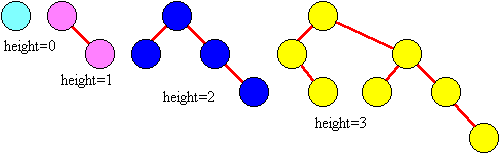
实际上,二叉查找树操作的运行时间与树的高度(Height)是有关系的。一个树的高度指的是从树的根开始所能到达的最长的路径长度。树的高度可被递归性地定义为:
- 如果节点没有子节点,则高度为 0;
- 如果节点只有一个子节点,则高度为该子节点的高度加 1;
- 如果节点有两个子节点,则高度为两个子节点中高度较高的加 1;
计算树的高度要从叶子节点开始,首先将叶子节点的高度置为 0,然后根据上面的规则向上计算父节点的高度。以此类推直到树中所有的节点高度都被标注后,则根节点的高度就是树的高度。
举例
下图显示了几棵不同的二叉查找树:
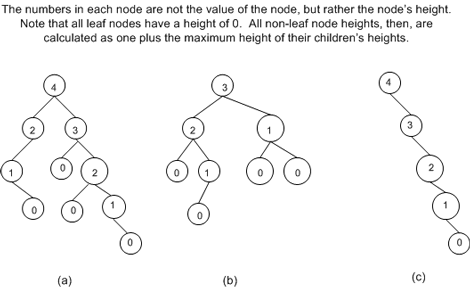
理想情况下,如果树中节点的数量为 n,则一棵满足平均时间复杂度为 $O(log_2n)$ 的二叉查找树的高度,应接近于比 $log_2n$ 小的最大整数。
树 (b)
上图中的三棵二叉查找树中,树 (b) 拥有最好的高度与节点数量的比例。树 (b) 的高度为 3 ,节点数量为 8,所以 $log_28$ = 3,结果正好与树的高度相等。
树 (a)
树 (a) 的节点数量为 10,而高度为 4,$log_210$ = 3.3219,比 3.3219 小的最大整数是 3,所以树 (a) 最理想的高度应该为 3。我们可以通过移动距离最远的节点到中间的某个非叶子节点,以减少数的高度,以使该树的高度与节点数量的比例达到最优。
树 (c)
树 (c) 的情况是最差的,它的节点数量是 5,所以$log_25$ = 2.3219,则理想高度为 2,但实际上是 4。
分析
实际上,我们真正面对的问题,是如何保证二叉查找树的拓扑结构始终保持树高度与节点数量的最佳比例。
插入的顺序影响二叉查找树的构造
因为二叉查找树的拓扑结构与节点的插入顺序息息相关。同样的数据集合, 插入二叉搜素树中的顺序的不同,树的形状和结构也是不同的。
以put方法为例,我们重复调用它, 用key为1, 2, 3, 4的结点构造一颗二叉查找树。那么这颗二叉查找树的形状取决于不同的key的插入顺序。
**如果按照完全正序或者逆序输入, 二叉查找树的形状就会走向一个不好的极端:**如果按照 1 -> 2 -> 3 -> 4 的顺序插入, 那么这颗二叉树在形状上会变得像一颗单链表!
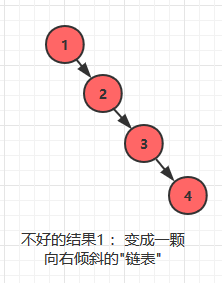
同样,如果按照4 -> 3 -> 2 ->1 的顺序插入, 它在形状上会变成一颗向左倾斜的链表
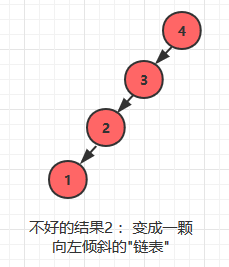
为什么二叉查找树会变得低效?
二叉查找树查找的原理和二分查找类似,就是借助于它本身的结构,在遍历查找的过程中跳过一些不必要的结点的比较,从而实现高效的查找。 BST的其他API也是借助了这一优势实现性能的飞跃。但是,在这种情况下, 查找一个结点将要像链表一样遍历它经过的所有结点, 二叉查找树的高效之源已经丧失了。 这就是最坏的情况。
插入和删除操作都可能降低未来操作的性能
上面只描述了插入操作对二叉树形状和操作性能的影响。而事实上,删除操作的效果也有类似之处: 可能使得原来分布得比较均匀的结点, 在删除部分结点之后,整体的分布变得不均匀了,并影响到未来操作的性能。
总结
综上所述,我们希望在进行动态操作(插入和删除)之后,能够通过一些指标,对二叉树的形状变化进行监督, 当发现树的形状开始变得不平衡的时候, 立即修正二叉树的形状。
通过这种方式, 不断地使得二叉树的形状和构造一直维持着一个**“平衡(balanced)”的状态,这种能够始终维持树平衡状态的二叉查找树称为自平衡二叉查找树(self-balancing binary search tree)**。
自平衡二叉查找树(Self-balancing Binary Search Tree)
自平衡二叉查找树(Self-balancing Binary Search Tree),也称为**(自)平衡二叉搜索树**、或者(自)平衡二叉树。
一棵平衡树指的是树能够保持其高度与广度能够保持预先定义的比例。不同的数据结构可以定义不同的比例以保持平衡,但所有的比例都趋向于$log_2n$。那么,一颗自平衡的二叉查找树也同样呈现出 $O(log_2n)$ 的平均时间复杂度。
Reference
- 自平衡二叉查找树 - https://www.cnblogs.com/gaochundong/p/self_balancing_binary_search_tree.html
- 一篇搞懂AVL平衡二叉树 - https://zhuanlan.zhihu.com/p/34840762、
- 【算法】论平衡二叉树(AVL)的正确种植方法 - https://www.cnblogs.com/penghuwan/p/8166133.html