二叉查找树（Binary Search Tree，BST）

二叉查找树（Binary Search Tree），也称为二叉搜索树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者一颗二叉树的任何节点均满足：

若节点的左子树不空，则左子树上所有节点的值均小于这个节点的值；
若节点的右子树不空，则右子树上所有节点的值均大于这个节点的值；
节点的左、右子树也分别为二叉查找树；
没有值相等的节点

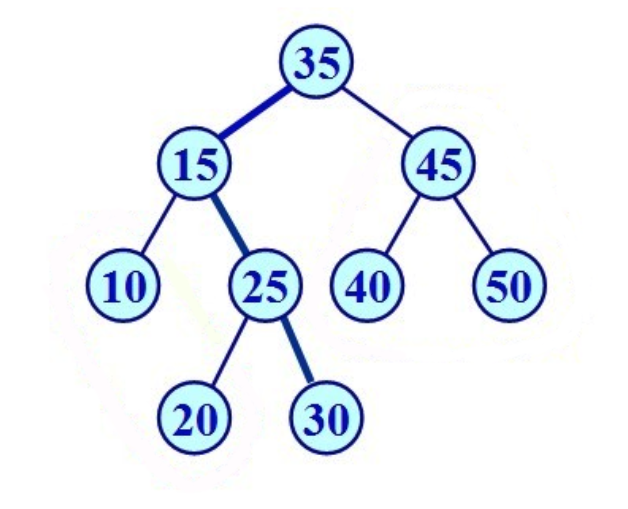
如果对一棵二叉查找树进行中序遍历，会得到一个已经将各结点的值按从小到大的顺序排列好的序列，所以也称二叉查找树为二叉排序树。

比如，对上面的二叉查找树进行中序遍历，结果为：10 15 20 25 30 35 40 45 50。

二叉查找树的意义

二分查找很好的解决了查找问题，将时间复杂度从 $O (n)$ 降到了 $O (l o g_{2} n)$ 。但是二分查找的前提条件是数据必须是有序的，并且具有线性的下标。对于线性表，可以很好的应用二分查找，但是在插入和删除操作时则可能会造成整个线性表的动荡，时间复杂度达到了 $O (n)$ 。

链表更是没法应用二分查找。

于是我们引入二叉查找树，在理想情况下，其在查找、插入、删除都能够达到 $O (l o g_{2} n)$ 的时间复杂度。

性能分析

在二叉查找树中查找节点，理想情况下，每次检查后，待检查的节点数都会减半。

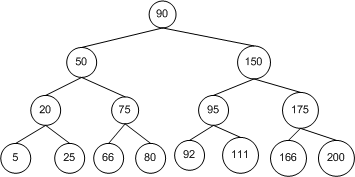
如下图中的二叉查找树，包含了 15 个节点。从根节点开始执行查找算法，第一次比较决定我们是移向左子树还是右子树。对于任意一种情况，一旦执行这一步，我们需要访问的节点数就减少了一半，从 15 降到了 7。同样，下一步访问的节点也减少了一半，从 7 降到了 3，以此类推。

根据这一特点，查找算法的时间复杂度应该是 $O (l o g _{2} n)$ ，简写为 $O (l g n)$ 。 $l o g _{2} n = y$ ，相当于 2y = n。即，如果节点数量增加 n，查找时间只缓慢地增加到 $l o g _{2} n$ 。

下图中显示了 $O (l o g_{} 2 n)$ 和线性增长 $O (n)$ 的增长率之间的区别。时间复杂度为 $O (l o g _{2} n)$ 的算法运行时间为下面那条线。

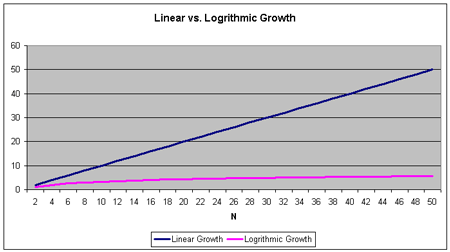
从上图可以看出， $O (l o g _{2} n)$ 曲线几乎是水平的，随着 n 值的增加，曲线增长十分缓慢。举例来说，查找一个具有 1000 个元素的数组，需要查询 1000 个元素，而查找一个具有 1000 个元素的二叉查找树，仅需查询不到10 个节点（ $l o g_{2} 1024$ = 10）。

而实际上，对于二叉查找树查找算法来说，其十分依赖于树中节点的拓扑结构，也就是节点间的布局关系。下图描绘了一个节点插入顺序为 20, 50, 90, 150, 175, 200 的二叉查找树。这些节点是按照递升顺序被插入的，结果就是这棵树没有广度（Breadth）可言。也就是说，它的拓扑结构其实就是将节点排布在一条线上，而不是以扇形结构散开，所以查找时间也为 O(n)。

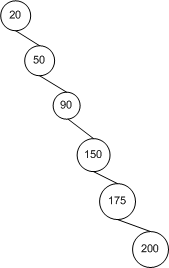
当二叉查找树中的节点以扇形结构散开时，对它的插入、删除和查找操作最优的情况下可以达到亚线性的运行时间 $O (l o g_{2} n)$ 。因为当在 BST 中查找一个节点时，每一步比较操作后都会将节点的数量减少一半。尽管如此，如果拓扑结构像上图中的样子时，运行时间就会退减到线性时间 O(n)。因为每一步比较操作后还是需要逐个比较其余的节点。也就是说，在这种情况下，在二叉查找树中查找节点与在数组（Array）中查找就基本类似了。

因此，二叉查找树查找时间依赖于树的拓扑结构。最佳情况是 $O (l o g _{2} n)$ ，而最坏情况是 O(n)。

总结

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低，在理想情况下，均为 $O (l o g_{2} n)$ 。

查找：理想情况/平均情况 $O (l o g_{2} (n))$ ，最坏情况 $O (n)$ 。
插入：理想情况/平均情况 $O (l o g_{2} (n))$ ，最坏情况 $O (n)$ 。
删除：理想情况/平均情况 $O (l o g_{2} (n))$ ，最坏情况 $O (n)$ 。

二叉查找树的常用操作

查找节点

查找指定值的元素

在二叉查找树bb中查找xx的过程为：

若b是空树，则搜索失败，否则：
若x等于b的根节点的数据域之值，则查找成功；否则：
若x小于b的根节点的数据域之值，则递归搜索左子树；否则:
递归查找右子树

使用python实现如下：

def search(root, val):
    if root == None:
        return False, None
    elif val > root.val:
        return search(root.right, val)
    elif val < root.val:
        return search(root.left, val)
    else:
        return True, root

查找最小值

# recursion
def smallest(self, root: Optional[TreeNode]) -> int:
    if not root:
      return -1
		def dfs(root):
			if not root.left:
				return root.val
			return dfs(root.left)

		return dfs(root)
  
# iterative
def minValue(root):
  if not root:
      return -1
  curr = root
  while curr and curr.left:
    curr = curr.left
  return curr

查找最大值

	def biggest(self, root: Optional[TreeNode]) -> int:
    if not root:
      return -1
		def dfs(root):
			if not root.right:
				return root.val
			return dfs(root.right)

		return dfs(root)

插入节点

向一个二叉查找树b中插入一个节点s，过程为：

若b是空树，则将s所指结点作为根节点插入，否则：
若s.val等于b的根节点的数据域之值，则返回，否则：
若s.val小于b的根节点的数据域之值，则把s所指节点插入到左子树中，否则：
把s所指节点插入到右子树中（新插入节点总是叶子节点）

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def insertIntoBST(root, val):
    """
    :param root: TreeNode | None  (BST 的根节点)
    :param val:  int             (要插入的值)
    :return: TreeNode           (插入新值后，BST 的根节点)
    """
    # 如果根节点为空，新建节点作为根返回
    if root is None:
        return TreeNode(val)

    # 比较插入值和当前节点值
    if val < root.val:
        # 往左子树插入
        root.left = insertIntoBST(root.left, val)
    else:
        # val >= root.val 的情况，这里选择插入到右子树
        root.right = insertIntoBST(root.right, val)

    return root

删除节点

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def minValueNode(root):
    curr = root
    while curr and curr.left:
        curr = curr.left
    return curr

# time: O(logn) 
def remove(root, val):
    if not root:
        return None

    if val > root.val:
        root.right = remove(root.right, val)
    elif val < root.val:
        root.left = remove(root.left, val)
    else:
        # 找到要删除的节点
        if not root.left:
            # 左子树为空，用右子树替代
            return root.right
        elif not root.right:
            # 右子树为空，用左子树替代
            return root.left
        else:
            # 左右子树均不为空时，找到右子树中的最小值节点
            minNode = minValueNode(root.right)
            # 将该最小值替换到当前节点上
            root.val = minNode.val
            # 然后在右子树中递归删除这个最小值节点
            root.right = remove(root.right, minNode.val)

    return root

二叉查找树的节点删除操作分以下三种情况。

Case 1 - 为叶子结点

如果待删除的节点是一个叶子节点，那么可以立即删除这个节点

例：删除值为16的节点，因为该节点是叶子节点，因此可以直接删除。

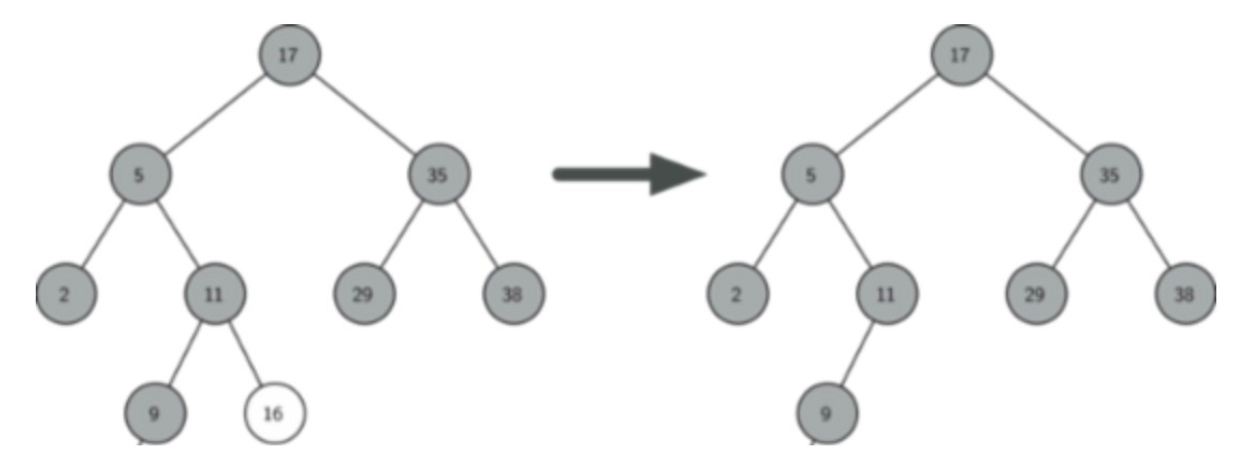
Case 2 - 有一个子节点

如果待删除节点有一个子节点，则要先将当前子节点对应的树上移到待删除节点的父节点下，再删除待删除节点

例：删除值为25的节点，而它下面有且只有一个子节点（这个子节点的值为35）。则在删除前，需要先将该子节点上移到待删除节点的父节点下（该父节点的值为17）。

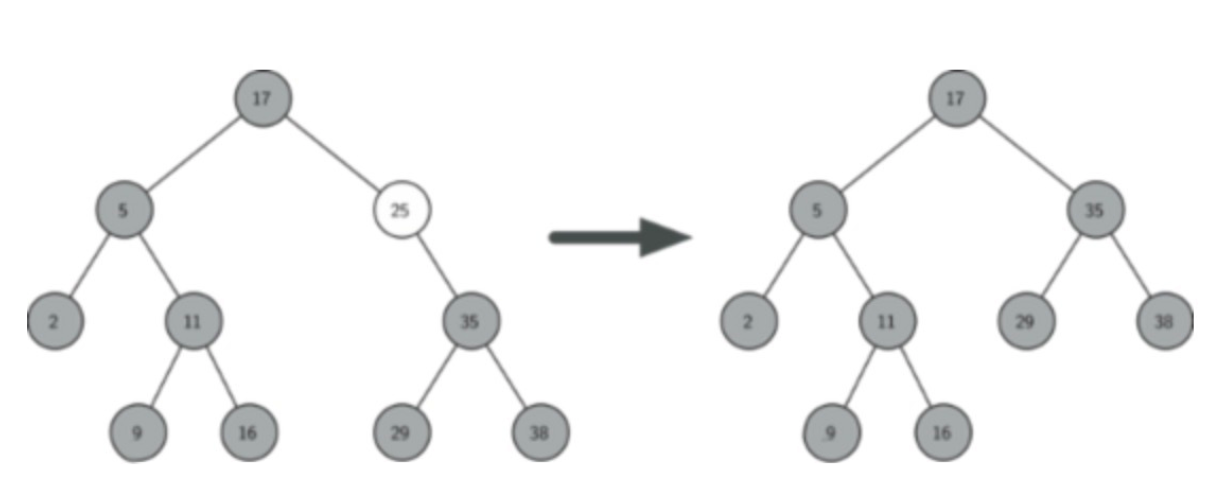
Case 3 - 有两个子节点

如果待删除节点有两个子节点，则将其右子树的最小值代替此节点的数据，并将其右子树的具有最小值的节点删除

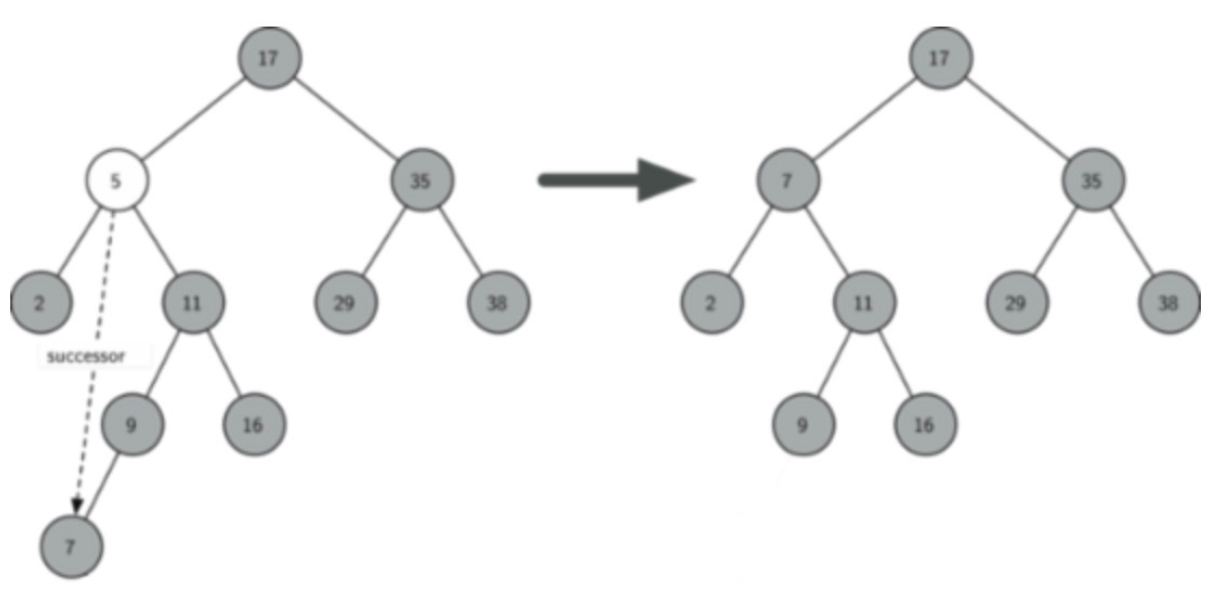
例：删除值为5的节点，要先找到待删除节点的右子树中的最小节点（在这个过程中，用一个临时变量successor，以存储在值为5的节点的右子树中搜索到的最小节点），我们发现，待删除节点的右子树中的最小节点为7，因此用最小节点7替换被删除节点，再删除之前的最小节点7，以维持二叉树结构。

Reference

https://en.wikipedia.org/wiki/Binary_search_tree

【Data Structure】二叉查找树（Binary Search Tree）