二叉树(Binary Tree)
简单地理解,满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
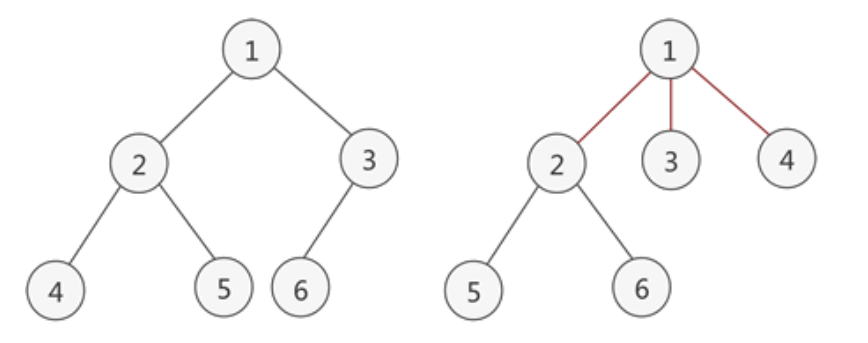
-
节点
- 节点(Node):树中存储数据和结构信息的基本单元。
- 叶节点(Leaf):没有任何子节点(Child)的节点,也称“外部节点”。
- 根节点(Root):树的最顶层节点,没有父节点(Parent)。
- 子节点(Child):某个节点所直接指向的下层节点。二叉树中特别区分为 左子节点(Left Child) 和 右子节点(Right Child)。
- 父节点(Parent):某个节点的上层节点;若A是B的子节点,则B是A的父节点。
- 兄弟节点(Sibling):同一个父节点下的多个子节点互为兄弟关系。二叉树里往往指“左子节点”和“右子节点”之间的关系。
-
子树(Subtree):以某个节点作为根节点的所有后代节点构成的一棵新树。例如,某个节点的左子树、右子树分别是该节点的左孩子(及其所有后代)和右孩子(及其所有后代)。
-
Depth / Height / Level(深度、高度、层级)
- 深度(Depth)
- 某个节点相对于 根节点 的距离(边的条数)或层数。
- 根节点的深度一般定义为 0;若 A 是 B 的子节点,则 depth(A) = depth(B) + 1。
- 高度(Height)
- 某个节点的高度:从该节点到其 最远叶节点 的边数。若为叶节点,其高度为 0。
- 整棵树(根节点)的高度:从根节点到最远叶节点的边数。部分教材中也会将“高度”称作“深度”,需注意差异。
- 层级(Level)
- 有时用于表示与根节点的距离,或作为深度的同义词。通常根节点所在的层记为第 1 层(或第 0 层),依次向下递增。
- 深度(Depth)
-
路径(Path):在树中,一系列相连节点组成的序列,比如从一个节点沿着边逐级到达另一个节点的过程。
-
Degree(度):一个节点拥有的子节点个数。二叉树中每个节点的度不超过 2。
-
Ancestors / Descendants(祖先 / 后代):若节点 A 在从根到节点 B 的路径上出现,则 A 是 B 的祖先;B 是 A 的后代。
-
LCA(Lowest Common Ancestor,最近公共祖先):对两个节点来说,与它们都有关联的祖先节点中,层级(深度)最大的那一个。
二叉树的性质
经过前人的总结,二叉树具有以下几个性质:
- 性质1:二叉树中,第 i 层最多有$2^{i-1}$ 个结点。
- 性质2:如果二叉树的深度为 K,那么此二叉树最多有 $2^K-1$ 个结点(k>=1)。
- 性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
- 性质4:在任意一棵二叉树中,若叶子结点的个数为$n_0$,度为2的结点数为$n_2$,则$n_0=n_2+1$。
二叉树还可以继续分类,衍生出满二叉树和完全二叉树。
性质1:二叉树第i层上的结点数目最多为 $2^{i-1}$ (i≥1)
证明:下面用"数学归纳法"进行证明。
(01) 当i=1时,第i层的节点数目为 $2^{i-1}=2^{0}=1$。因为第1层上只有一个根结点,所以命题成立。
(02) 假设当i>1,第i层的节点数目为 $2^{i-1}$。这个是根据(01)推断出来的!
下面根据这个假设,推断出"第(i+1)层的节点数目为 $2^{i}$ “即可。
由于二叉树的每个结点至多有两个孩子,故"第(i+1)层上的结点数目” 最多是 “第i层的结点数目的2倍”。即,第(i+1)层上的结点数目最大值 $=2×2^{i-1}=2^{i}$。
故假设成立,原命题得证!
性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)
证明:在具有相同深度的二叉树中,当每一层都含有最大结点个数时,其二叉树中结点数最多。利用"性质1"可知,深度为k的二叉树的结点数至多为:
$2^0+2^1+…+2^{k-1}=2^{k}-1$
故原命题得证!
性质3:包含n个结点的二叉树的高度至少为 $log_2 (n+1)$
证明:根据"性质2"可知,高度为h的二叉树最多有 $2^{h}–1$ 个结点。反之,对于包含n个节点的二叉树的高度至少为 $log_2(n+1)$。
性质4:在任意一棵二叉树中,若叶子结点的个数为 $n_0$,度为2的结点数为 $n_2$,则$n_0=n_2+1$
证明:因为二叉树中所有结点的度数均不大于2,所以结点总数(记为n)=“0度结点数(n0)” + “1度结点数(n1)” + “2度结点数(n2)"。由此,得到等式一。
(等式一) $n=n_0+n_1+n_2$
另一方面,0度结点没有孩子,1度结点有一个孩子,2度结点有两个孩子,故二叉树中孩子结点总数是:$n_1+2n_2$。此外,只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
(等式二) $n=n_1+2n_2+1$
由(等式一)和(等式二)计算得到:$n_0=n_2+1$。原命题得证!
满二叉树(Full Binary Tree)
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
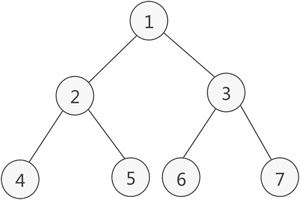
如上图所示就是一棵满二叉树。
又称“严格二叉树(Strict Binary Tree)”,每个节点要么没有子节点、要么恰好有两个子节点(不存在只有一个子节点的情况)。
完全二叉树(Complete Binary Tree)
除最后一层外,每一层上的节点都达到最大个数,而且最后一层的节点在左侧尽量紧密排列。
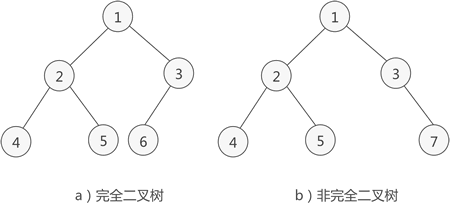
如上图所示是一棵完全二叉树,图 b) 由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树。
完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 ⌊$log_2n$⌋+1。
⌊$log_2n$⌋ 表示取小于 $log_2n$ 的最大整数。例如,⌊$log_24$⌋ = 2,而 ⌊$log_25$⌋ 结果也是 2。
对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号(如上图),对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
- 当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
- 如果 2*i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2*i 。
- 如果 $2i+1>n$ ,则结点 i 肯定没有右孩子;否则右孩子是结点 $2i+1$ 。
完全二叉树的编号问题
以上是将根结点编号为0的规律,比较符合数组下标以0开始的访问方式。有另外的一些以1开始的规律,虽然不是错的,但是不太适合写代码:
若结点的高度为h,则该结点的左儿子是2*h,右儿子是左儿子加1,即2*h+1。反过来,如果儿子的编号为y,则父结点的编号是(int)x/2。高度h的规律,其实是上面的树的编号从1开始,而不是从0开始。
所以问题也来了,树的编号从0开始,从1开始,从n开始呢,表达式是怎样呢。直观上可以知道,结点和儿子的关系是不变的,变的只是编号,所以应该可以利用其中一个规律推导出编号改变后的表达式。
首先,把完全二叉树用数组的形式表示: 0 开始:0 1 2 3 4 5 6 7… 1 开始:1 2 3 4 5 6 7… 2 开始:2 3 4 5 6 7…
可以看出,总体编号是往左移的。以编号0开始为例,左儿子为x,右儿子为y,当前结点为k,那么规律是x = 2*k + 1和y = 2*k + 2,其中x、y、k都是数组里面的元素。
当以编号1开始时,总体编号相当于往左移动了1位。其中,相当于x往左移动了1位,相当于y向左移动了1位,k也往左移动了1位,因为它们都是数组里面的元素。
设新的关系,左儿子为x1,右儿子为y1,当前结点为k1,那么得到关系x1 - 1 = x、y1 - 1 = y和k1 - 1 = k,代入编号为0的表达式:
x = 2*k + 1 => x1 - 1 = 2*(k1 - 1) + 1 推导出 x1 = 2*k1
y = 2*k + 2 => y1 - 1 = 2*(k1 - 1) + 2 推导出 y1 = 2*k1 + 1。也可以直接使用右儿子 = 左儿子 + 1直接得出。
所以,也即是说,当编号从1开始,结点与儿子结点的关系是x = 2k和y = 2k+1,这和高度h那里得到的表达式一致。
当编号从n开始,就相当于数组往左移动了n位,思路参考上面,和高中数学里移动x、y坐标轴一样(没想到是高中数学)。
二叉树的存储结构
二叉树的存储结构有两种,分别为顺序存储和链式存储。
二叉树的顺序存储结构
二叉树的顺序存储,指的是使用**顺序表(数组)**存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
有读者会说,满二叉树也可以使用顺序存储。要知道,满二叉树也是完全二叉树,因为它满足完全二叉树的所有特征。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如下图所示:
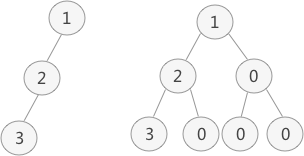
上图中,左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。
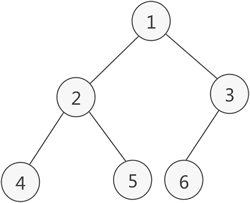
例如,存储上图所示的完全二叉树,其存储状态如下图所示:


同样,存储由普通二叉树转化来的完全二叉树也是如此。例如,上图中普通二叉树的数组存储状态如下图所示:

由此,我们就实现了完全二叉树的顺序存储。
不仅如此,从顺序表中还原完全二叉树也很简单。我们知道,完全二叉树具有这样的性质,将树中节点按照层次并从左到右依次标号(1,2,3,…),若节点 i 有左右孩子,则其左孩子节点为 2*i,右孩子节点为 2*i+1。此性质可用于还原数组中存储的完全二叉树。
二叉树的链式存储结构
其实二叉树并不适合用数组存储,因为并不是每个二叉树都是完全二叉树,普通二叉树使用顺序表存储或多或多会存在空间浪费的现象。
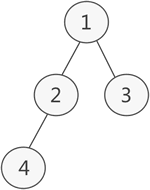
如上图所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。因此,上图对应的链式存储结构如下图所示:
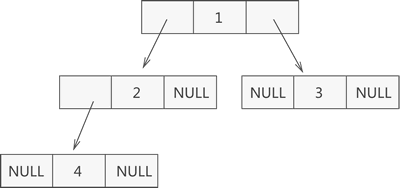
由上图可知,采用链式存储二叉树时,其节点结构由 3 部分构成(如下图所示):
- 指向左孩子节点的指针(Lchild);
- 节点存储的数据(data);
- 指向右孩子节点的指针(Rchild);

三叉链表
其实,二叉树的链式存储结构远不止上图所示的这一种。例如,在某些实际场景中,可能会做 “查找某节点的父节点” 的操作,这时可以在节点结构中再添加一个指针域,用于各个节点指向其父亲节点,如下图所示:
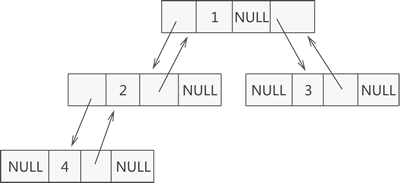
这样的链表结构,通常称为三叉链表。
Reference
- 数据结构概述 - http://data.biancheng.net/intro/