图(Graph)
我们知道,数据之间的关系有 3 种,分别是 “一对一”、“一对多” 和 “多对多”,前两种关系的数据可分别用线性表和树结构存储,本节学习存储具有"多对多"逻辑关系数据的结构——图存储结构。
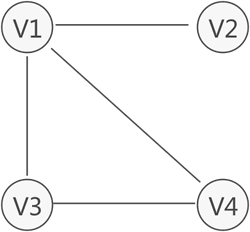
上图所示为存储 V1、V2、V3、V4 的图结构,从图中可以清楚的看出数据之间具有的"多对多"关系。例如,V1 与 V4 和 V2 建立着联系,V4 与 V1 和 V3 建立着联系,以此类推。
与链表不同,图中存储的各个数据元素被称为顶点(而不是节点)。拿图 1 来说,该图中含有 4 个顶点,分别为顶点 V1、V2、V3 和 V4。
图存储结构中,习惯上用 Vi 表示图中的顶点,且所有顶点构成的集合通常用 V 表示,如图 1 中顶点的集合为 V={V1,V2,V3,V4}。
注意,上面所展示的图仅是图存储结构的其中一种,数据之间 “多对多” 的关系还可能用如下图所示的图结构表示:
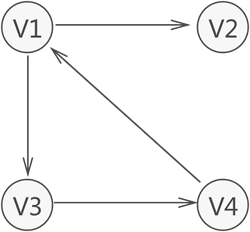
可以看到,各个顶点之间的关系并不是"双向"的。比如,V4 只与 V1 存在联系(从 V4 可直接找到 V1),而与 V3 没有直接联系;同样,V3 只与 V4 存在联系(从 V3 可直接找到 V4),而与 V1 没有直接联系,以此类推。
因此,图存储结构可细分两种表现类型,分别为无向图(Undirected Graph)和有向图(Directed Graph)。
无向图(Undirected Graph)
边(edge)仅仅是两个顶点(vertex)之间的连接。为了和其他图模型相区别,我们将它称为无向图。这是一种最简单的图模型,我们先来看一下它的定义。
图是由一组顶点和一组能够将两个顶点相连的边组成的。
就定义而言,顶点叫什么名字并不重要,但我们需要一个方法来指代这些顶点。一般使用0至V-1 来表示一张含有 V 个顶点的图中的各个顶点。这样约定是为了方便使用数组的索引来编写能够高效 访问各个顶点中信息的代码。用一张符号表来为顶点的名字和 0 到 V-1 的整数值建立一一对应的关系并不困难,因此直接使用数组索引作为结点 的名称更方便且不失一般性(也不会损失什么效率)。我们用 v-w w-v 的记法来表示连接 v 和 w 的边, 是这条边的另一种表示方法。
在绘制一幅图时,用圆圈表示顶点,用连接两个顶点的线段表示边,这样就能直观地看出图的结构。但这种直觉有时也可能会误导我们,因为图的定义和绘出的图像是无关的。例如,下图中的两组图表示的是同一幅图,因为图的构成只有(无序的)顶点和边(顶点对)。
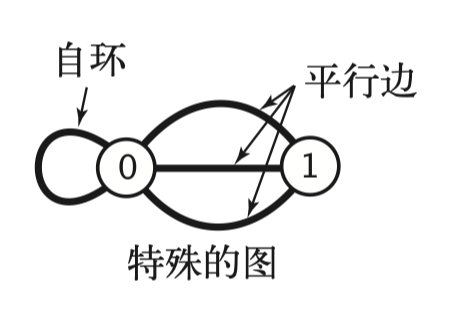
特殊的图。我们的定义允许出现两种简单而特殊的情况, 参见下图:
- 自环,即一条连接一个顶点和其自身的边;
- 平行边:连接同一对顶点的两条边。
无环图(Acyclic Graph)
无环图是一种不包含环的图。我们将要学习的几个算法就是要找出一幅图中满足一定条件的无环子图。
有向图(Directed Graph)
有向图的一个突出特点,边是单向的,即每条边所连接的两个顶点都是一个有序对。
图的基本常识
弧头和弧尾
有向图中,无箭头一端的顶点通常被称为"初始点"或"弧尾",箭头直线的顶点被称为"终端点"或"弧头"。
入度(InDegree)和出度(OutDegree)
对于有向图中的一个顶点 V 来说,箭头指向 V 的弧的数量为 V 的入度(InDegree,记为 ID(V));箭头远离 V 的弧的数量为 V 的出度(OutDegree,记为OD(V))。
拿下图中的顶点 V1来说,该顶点的入度为 1,出度为 2(该顶点的度为 3)。

(V1,V2) 和 <V1,V2> 的区别
无向图中描述两顶点(V1 和 V2)之间的关系可以用 (V1,V2) 来表示,而有向图中描述从 V1 到 V2 的"单向"关系用 <V1,V2> 来表示。
由于图存储结构中顶点之间的关系是用线来表示的,因此 (V1,V2) 还可以用来表示无向图中连接 V1 和 V2 的线,又称为边;同样,<V1,V2> 也可用来表示有向图中从 V1 到 V2 带方向的线,又称为弧。
集合 VR 的含义
并且,图中习惯用 VR 表示图中所有顶点之间关系的集合。例如,上面的无向图的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)},上面的有向图的集合 VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。
路径和回路
无论是无向图还是有向图,从一个顶点到另一顶点途径的所有顶点组成的序列(包含这两个顶点),称为一条路径。如果路径中第一个顶点和最后一个顶点相同,则此路径称为**“回路”(或"环")**。
并且,若路径中各顶点都不重复,此路径又被称为**“简单路径”;同样,若回路中的顶点互不重复,此回路被称为“简单回路”(或简单环)**。

拿上图来说,从 V1 存在一条路径还可以回到 V1,此路径为 {V1,V3,V4,V1},这是一个回路(环),而且还是一个简单回路(简单环)。
在有向图中,每条路径或回路都是有方向的。
权和网
在某些实际场景中,图中的每条边(或弧)会赋予一个实数来表示一定的含义,这种与边(或弧)相匹配的实数被称为**“权”,而带权的图通常称为网**,或者成为加权图(Weighted Graph)。如下图所示,就是一个网结构:
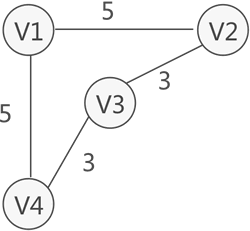
而带有权的有向图,就称为加权有向图(Weighted Directed Graph)。
子图:指的是由图中一部分顶点和边构成的图,称为原图的子图。
图存储结构的分类
根据不同的特征,图又可分为完全图,连通图、稀疏图和稠密图。
完全图
完全图:若图中各个顶点都与除自身外的其他顶点有关系,这样的无向图称为完全图(如下图)。同时,满足此条件的有向图则称为有向完全图(下图)。
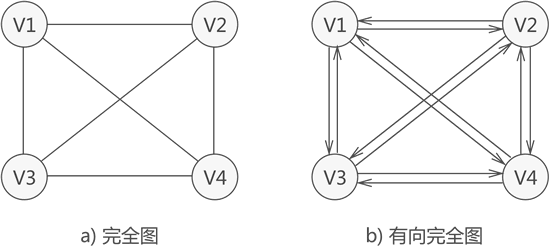
具有 n 个顶点的完全图,图中边的数量为 n(n-1)/2;而对于具有 n 个顶点的有向完全图,图中弧的数量为 n(n-1)。
稀疏图和稠密图
稀疏图和稠密图:这两种图是相对存在的,即如果图中具有很少的边(或弧),此图就称为**“稀疏图”;反之,则称此图为“稠密图”**。 稀疏和稠密的判断条件是:e<nlogn,其中 e 表示图中边(或弧)的数量,n 表示图中顶点的数量。如果式子成立,则为稀疏图;反之为稠密图。
连通图
图中从一个顶点到达另一顶点,若存在至少一条路径,则称这两个顶点是连通着的。例如下图中,虽然 V1 和 V3 没有直接关联,但从 V1 到 V3 存在两条路径,分别是 V1-V2-V3和 V1-V4-V3,因此称 V1 和 V3 之间是连通的。
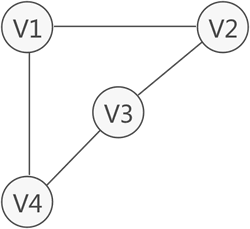
无向图中,如果任意两个顶点之间都能够连通,则称此无向图为连通图。例如,下图中的无向图就是一个连通图,因为此图中任意两顶点之间都是连通的。
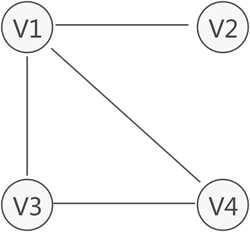
若无向图不是连通图,但图中存储某个子图符合连通图的性质,则称该子图为连通分量。
前面讲过,由图中部分顶点和边构成的图为该图的一个子图,但这里的子图指的是图中"最大"的连通子图(也称"极大连通子图")。
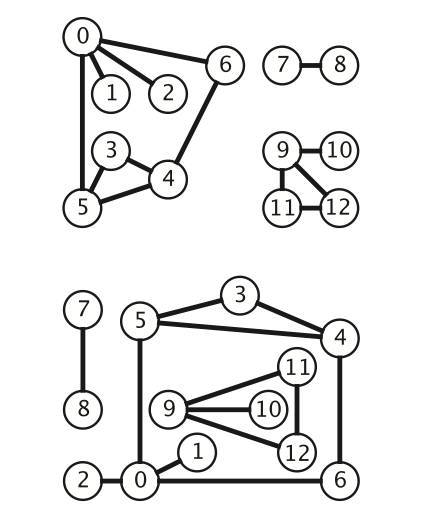
如下图所示,虽然下图 a) 中的无向图不是连通图,但可以将其分解为 3 个"最大子图"(图 b)),它们都满足连通图的性质,因此都是连通分量。
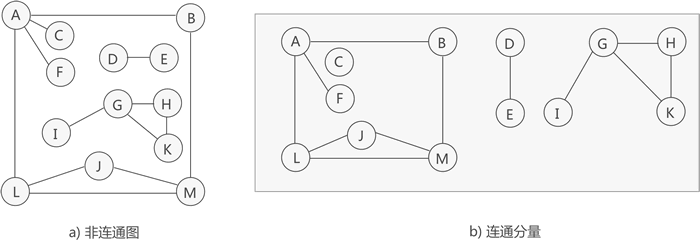
提示,图 a) 中的无向图只能分解为 3 部分各自连通的"最大子图"。
需要注意的是,连通分量的提出是以"整个无向图不是连通图"为前提的,因为如果无向图是连通图,则其无法分解出多个最大连通子图,因为图中所有的顶点之间都是连通的。
强连通图
有向图中,若任意两个顶点 Vi 和 Vj,满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通,也就是都含有至少一条通路,则称此有向图为强连通图。如下图所示就是一个强连通图。
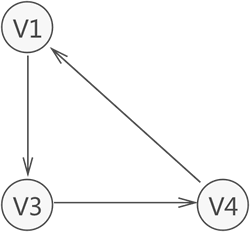
与此同时,若有向图本身不是强连通图,但其包含的最大连通子图具有强连通图的性质,则称该子图为强连通分量。
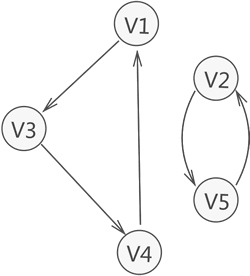
如图 5 所示,整个有向图虽不是强连通图,但其含有两个强连通分量。
总结
可以这样说,连通图是在无向图的基础上对图中顶点之间的连通做了更高的要求,而强连通图是在有向图的基础上对图中顶点的连通做了更高的要求。
无向图(Undirected Graph,简单连接)、有向图(Directed Graph,连接有方向性)、加权图(Weighted Graph,连接带有权值)和加权有向图(Weighted Directed Graph,连接既有方向性又带有权值)。
生成树和生成森林
生成树
对连通图进行遍历,过程中所经过的边和顶点的组合可看做是一棵普通树,通常称为生成树。
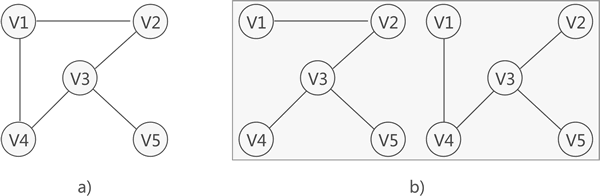
如上图所示,图 a) 是一张连通图,图 b) 是其对应的 2 种生成树。
注意,连通图中,由于任意两顶点之间可能含有多条通路,遍历连通图的方式有多种,往往一张连通图可能有多种不同的生成树与之对应。
连通图中的生成树必须满足以下 2 个条件:
- 包含连通图中所有的顶点;
- 任意两顶点之间有且仅有一条通路;
因此,连通图的生成树具有这样的特征,即生成树中边的数量 = 顶点数 - 1。
生成森林
生成树是对应连通图来说,而生成森林是对应非连通图来说的。
我们知道,非连通图可分解为多个连通分量,而每个连通分量又各自对应多个生成树(至少是 1 棵),因此与整个非连通图相对应的,是由多棵生成树组成的生成森林。
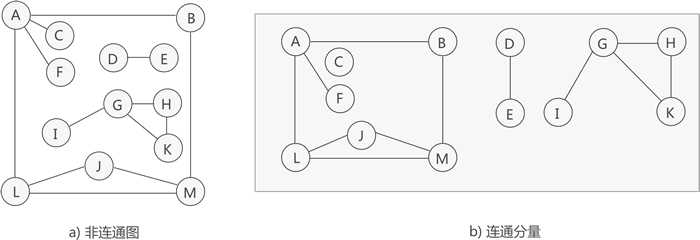
如上图所示,这是一张非连通图,可分解为 3 个连通分量,其中各个连通分量对应的生成树如下图所示:
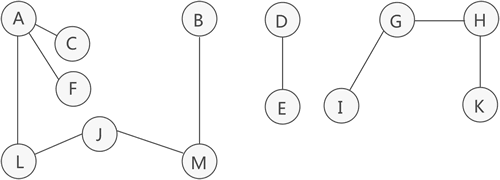
注意,上图中列出的仅是各个连通分量的其中一种生成树。
因此,多个连通分量对应的多棵生成树就构成了整个非连通图的生成森林。
Reference
- 《Algorithm》
- 数据结构概述 - http://data.biancheng.net/intro/