图的顺序存储方法 - 邻接矩阵(Adjacency Matrix)
使用数组存储图时,需要使用两个数组,一个数组存放图中顶点本身的数据(一维数组),另外一个数组用于存储各顶点之间的关系(二维数组)。
- 如果只是存储图中包含的顶点,使用一维数组就足够了;
- 然而,我们还需要存储顶点之间的关系,因此要记录每个顶点和其它所有顶点之间的关系,所以需要使用二维数组。
这个二维数组称为邻接矩阵(Adjacency Matrix)。
不同类型的图,存储的方式略有不同,根据图有无权,可以将图划分为两大类:图和网 。
图,包括无向图和有向图;网,是指带权的图,包括无向网和有向网。
存储方式的不同,指的是:在使用二维数组存储图中顶点之间的关系时,如果顶点之间存在边或弧,在相应位置用 1 表示,反之用 0 表示;如果使用二维数组存储网中顶点之间的关系,顶点之间如果有边或者弧的存在,在数组的相应位置存储其权值;反之用 0 表示。
无向图
我们来看一个无向图的实例,下图的左图就是一个无向图:
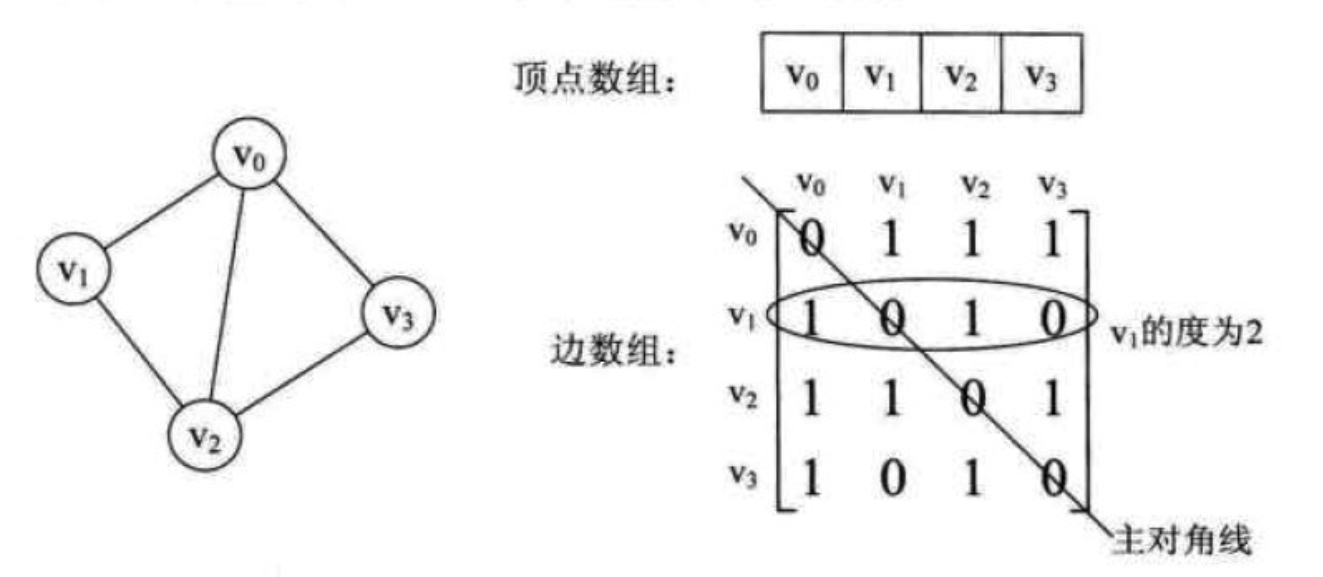
对于无向图来说,二维数组构成的邻接矩阵,实际上是对称矩阵。因此,在存储时就可以采用压缩存储的方式存储下三角或者上三角。
通过二阶矩阵,可以直观地计算出各个顶点的度,为该行(或该列)非 0 值的和。例如,第一行有两个 1,说明 V1 有两个边,所以度为 2。
有向图
我们再来看一个有向图的样例,如下图所示的左图:
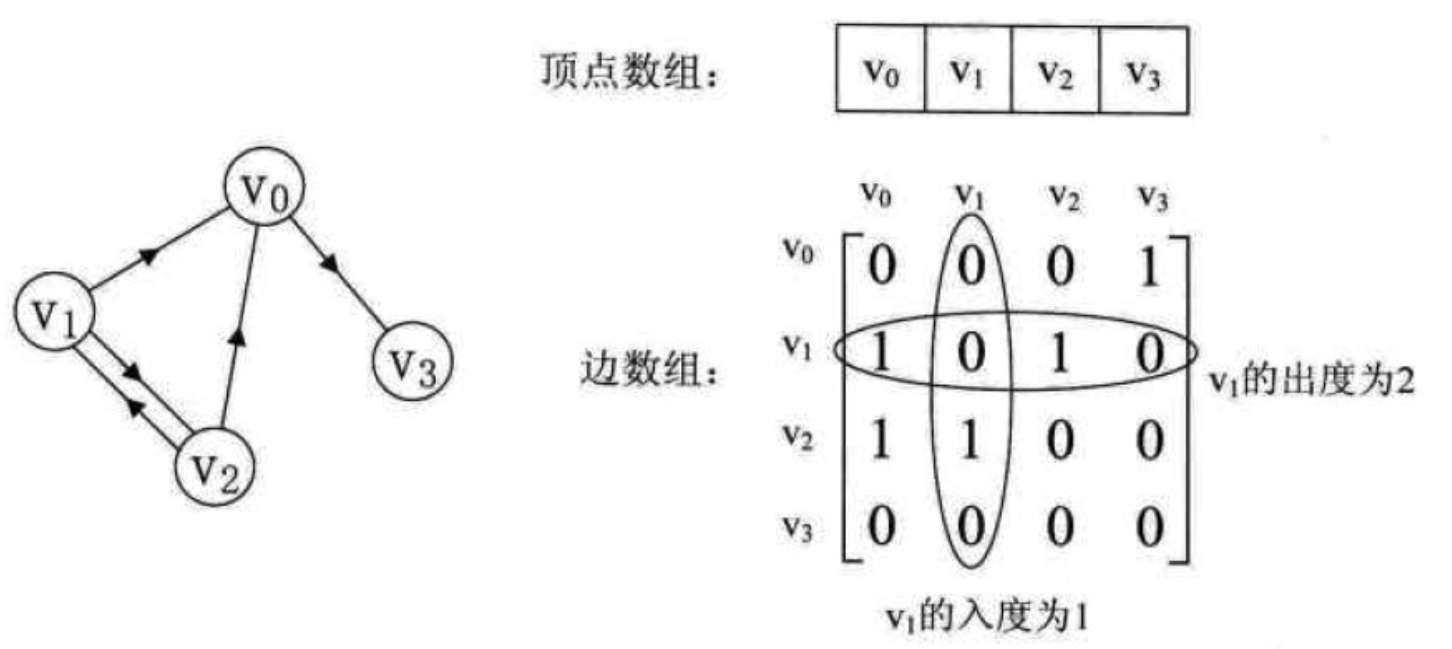
例如,arcs[0][1] = 1 ,证明从 V1 到 V2 有弧存在。且通过邻接矩阵,可以很轻松得知各顶点的出度和入度,出度为该行非 0 值的和,入度为该列非 0 值的和。例如,V1 的出度为 2 (因为第二行中有两个 1 ),为 2 ; V1 的入度为 1 (第二列中只有一个 1 )。
通常,图更多的是采用链表存储,具体的存储方法有 3 种,分别是:
- 邻接表
- 十字链表
- 邻接多重表
图的链式存储方法 - 邻接表(Adjacency List)
我们发现,当图中的边数相对于顶点较少时,使用邻接矩阵会对存储空间的极大浪费。我们可以考虑对边或弧使用链式存储的方式来解决空间浪费的问题。回忆树结构的孩子表示法,将结点存入数组,并对结点的孩子进行链式存储,不管有多少孩子,也不会存在空间浪费问题。
应用这种思路,我们把这种数组与链表相结合的存储方法称为邻接表(Adjacency List)。
邻接表既适用于存储无向图,也适用于存储有向图。
一些概念
邻接点
在具体讲解邻接表存储图的实现方法之前,先普及一个"邻接点“的概念。在图中,如果两个点相互连通,即通过其中一个顶点,可直接找到另一个顶点,则称它们互为邻接点。
邻接指的是图中顶点之间有边或者弧的存在。
邻接表
邻接表存储图的实现方式是,给图中的各个顶点独自建立一个链表,用节点存储该顶点,用链表中其他节点存储各自的邻接点。
与此同时,为了便于管理这些链表,通常会将所有链表的头节点存储到数组中(也可以用链表存储)。也正因为各个链表的头节点存储的是各个顶点,因此各链表在存储临界点数据时,仅需存储该邻接顶点位于数组中的位置下标即可。
例如,下图中的有向图,其对应的邻接表如下所示:
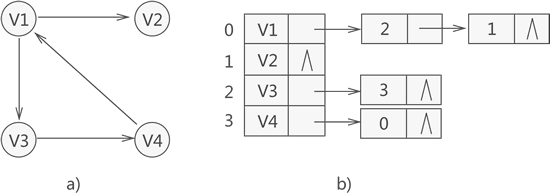
拿顶点 V1 来说,与其相关的邻接点分别为 V2 和 V3,因此存储 V1 的链表中存储的是 V2 和 V3 在数组中的位置下标 1 和 2。
从上图中可以看出,存储各顶点的节点结构分为两部分,数据域和指针域。数据域用于存储顶点数据信息,指针域用于链接下一个节点,如下图所示:

在实际应用中,除了上图这种节点结构外,对于用链接表存储网(边或弧存在权)结构,还需要节点存储权的值,因此需使用下图中的节点结构:

邻接表计算顶点的出度和入度
使用邻接表计算无向图中顶点的入度和出度会非常简单,只需从数组中找到该顶点然后统计此链表中节点的数量即可。
而使用邻接表存储有向图时,通常各个顶点的链表中存储的都是以该顶点为弧尾的邻接点,因此通过统计各顶点链表中的节点数量,只能计算出该顶点的出度,而无法计算该顶点的入度。
对于利用邻接表求某顶点的入度,有两种方式:
- 遍历整个邻接表中的节点,统计数据域与该顶点所在数组位置下标相同的节点数量,即为该顶点的入度;
- 建立一个逆邻接表,该表中的各顶点链表专门用于存储以此顶点为弧头的所有顶点在数组中的位置下标。比如说,建立一张上图a) 对应的逆邻接表,如下图所示:
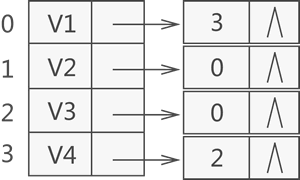
对于具有 n 个顶点和 e 条边的无向图,邻接表中需要存储 n 个头结点和 2e 个表结点。在图中边或者弧稀疏的时候,使用邻接表要比前一节介绍的邻接矩阵更加节省空间。
图的链式存储方法 - 十字链表
与邻接表不同,十字链表法仅适用于存储有向图和有向网。不仅如此,十字链表法还改善了邻接表计算图中顶点入度较为麻烦的问题。
十字链表存储有向图(网)的方式与邻接表有一些相同,都以图(网)中各顶点为首元节点建立多条链表,同时为了便于管理,还将所有链表的首元节点存储到同一数组(或链表)中。
其中,建立一个链表,用于存储顶点的首元节点的结构如下图所示:

从上图可以看出,首元节点中有一个数据域和两个指针域(分别用 firstin 和 firstout 表示):
- firstin 指针用于连接以当前顶点为弧头的其他顶点构成的链表;
- firstout 指针用于连接以当前顶点为弧尾的其他顶点构成的链表;
- data 用于存储该顶点中的数据;
由此可以看出,十字链表实质上就是为每个顶点建立两个链表,分别存储以该顶点为弧头的所有顶点和以该顶点为弧尾的所有顶点。
注意,存储图的十字链表中,各链表中首元节点与其他节点的结构并不相同,图 1 所示仅是十字链表中首元节点的结构,链表中其他普通节点的结构如图 2 所示:
十字链表中普通节点的结构示意图 图 2 十字链表中普通节点的结构示意图
从图 2 中可以看出,十字链表中普通节点的存储分为 5 部分内容,它们各自的作用是:
- tailvex 用于存储以首元节点为弧尾的顶点位于数组中的位置下标;
- headvex 用于存储以首元节点为弧头的顶点位于数组中的位置下标;
- hlink 指针:用于链接下一个存储以首元节点为弧头的顶点的节点;
- tlink 指针:用于链接下一个存储以首元节点为弧尾的顶点的节点;
- (info 指针:用于存储与该顶点相关的信息,例如量顶点之间的权值;)
比如说,用十字链表存储图 3a) 中的有向图,存储状态如图 3b) 所示:
十字链表存储有向图示意图 图 3 十字链表存储有向图示意图
拿图 3 中的顶点 V1 来说,通过构建好的十字链表得知,以该顶点为弧头的顶点只有存储在数组中第 3 位置的 V4(因此该顶点的入度为 1),而以该顶点为弧尾的顶点有两个,分别为存储数组第 1 位置的 V2 和第 2 位置的 V3(因此该顶点的出度为 2)。
对于图 3 各个链表中节点来说,由于表示的都是该顶点的出度或者入度,因此没有先后次序之分。
图的链式存储方法 - 邻接多重表
Reference
- 数据结构概述 - http://data.biancheng.net/intro/
- 《Algorithm》
- 《大话数据结构》