哈希表（Hash table）
哈希表（Hash table，也叫散列表），是根据键（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数（Hash function），存放元素的数组称做散列表（Hash table）。
一个通俗的例子是，为了查找电话簿中某人的号码，可以创建一个按照人名首字母顺序排列的表（即建立人名 x 到首字母 F(x) 的一个函数关系），在首字母为W的表中查找“王”姓的电话号码，显然比查找包含所有人电话的电话簿就要快得多。这里使用人名作为关键字（或者说键，Key），“取首字母”是这个例子中散列函数的函数法则 F()，存放首字母的表对应散列表（Hash table）。关键字和函数法则理论上可以任意确定。
哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制，那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1)；如果没有时间限制，那么我们可以使用无序数组并进行顺序查找，这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。
In many situations, hash tables turn out to be on average more efficient than search trees or any other table lookup structure. For this reason, they are widely used in many kinds of computer software, particularly for associative arrays, database indexing, caches, and sets.
散列函数/哈希函数（Hash Function）
上面已经提到了，将一个元素的键（Key，或者说元素的特征）转换为存放元素的数组（即散列表）中对应下标的函数就是散列函数（Hash Function）。
散列函数能使对一个数据序列的访问过程更加迅速有效，通过散列函数，数据元素将被更快定位。
而在实际中，元素的键并不一定都是数字，有可能是字符串，还有可能是几个值的组合等，所以我们需要实现自己的散列函数。
整数
直接定址法
取关键字或关键字的某个线性函数值为散列地址。即 hash(k)=k或 hash(k)=ak+b，其中 a，b为常数（这种散列函数叫做自身函数）。
平方取中法
取元素的键平方后的中间几位为哈希地址。
假如有以下关键字序列{421，423，436}，平方之后的结果为{177241，178929，190096}，那么可以取中间的两位数{72，89，00}作为Hash地址。
通常在选定哈希函数时不一定能知道关键字的全部情况，取其中的哪几位也不一定合适，而一个数平方后的中间几位数和数的每一位都相关，由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
折叠法
将元素的键拆分成几部分，然后将这几部分组合在一起，以特定的方式进行转化形成Hash地址。
假如知道图书的ISBN号为8903-241-23，可以将address(key)=89+03+24+12+3作为Hash地址。
除留取余法
如果知道Hash表的最大长度为m，可以取不大于m的最大质数p，然后对关键字进行取余运算，address(key)=key%p。
在这里p的选取非常关键，p选择的好的话，能够最大程度地减少冲突，p一般取不大于m的最大质数。
字符串
将字符串作为键的时候，我们也可以将他作为一个大的整数，采用保留除余法。我们可以将组成字符串的每一个字符取值然后进行哈希，比如
public int GetHashCode(string str)
{
char[] s = str.ToCharArray();
int hash = 0;
for (int i = 0; i < s.Length; i++)
{
hash = s[i] + (31 * hash);
}
return hash;
}
上面的哈希值是Horner计算字符串哈希值的方法，公式为:
举个例子，比如要获取”call”的哈希值，字符串c对应的unicode为99，a对应的unicode为97，L对应的unicode为108，所以字符串”call”的哈希值为
如果对每个字符去哈希值可能会比较耗时，所以可以通过间隔取N个字符来获取哈西值来节省时间，比如，可以 获取每8-9个字符来获取哈希值：
public int GetHashCode(string str)
{
char[] s = str.ToCharArray();
int hash = 0;
int skip = Math.Max(1, s.Length / 8);
for (int i = 0; i < s.Length; i+=skip)
{
hash = s[i] + (31 * hash);
}
return hash;
}
但是，对于某些情况，不同的字符串会产生相同的哈希值，这就是所谓的哈希冲突（Hash Collisions），比如下面的四个字符串：
如果我们按照每8个字符取哈希的话，就会得到一样的哈希值。
哈希冲突（Hash Collisions）
哈希冲突（Hash Collisions），也叫做哈希碰撞，意思是两个或者多个 key 映射到了哈希表的同一个位置。
处理哈希冲突的方式有两种：避免和解决，即冲突避免机制（Collision Avoidance）和冲突解决机制（Collision Resolution）。
避免哈希冲突的一个方法就是选择合适的哈希函数。哈希函数中的冲突发生的几率与数据的分布有关。
例如，如果社保号的后 4 位是随即分布的，则使用后 4 位数字比较合适。但如果后 4 位是以员工的出生年份来分配的，则显然出生年份不是均匀分布的，则选择后 4 位会造成大量的冲突。
我们将这种选择合适的哈希函数的方法称为冲突避免机制（Collision Avoidance）。
要知道，无论我们如何选择哈希函数，哈希冲突也不可能完全被避免（只是尽量减少其发生的频率）。因此，在冲突发生后，有很多策略可以实施，这些策略称为冲突解决机制（Collision Resolution）。
Hash表大小的确定
同时，Hash表大小的确定也非常关键，如果Hash表的空间远远大于最后实际存储的记录个数，则造成了很大的空间浪费，如果选取小了的话，则容易造成哈希冲突。
在实际情况中，一般需要根据最终记录存储个数和关键字的分布特点来确定Hash表的大小。还有一种情况时可能事先不知道最终需要存储的记录个数，则需要动态维护Hash表的容量，此时可能需要重新计算Hash地址。
哈希冲突解决机制（Hash Collision Resolution）
为了知道冲突产生的相同散列函数地址所对应的关键字，必须选用另外的散列函数，或者对冲突结果进行处理。而不发生冲突的可能性是非常之小的，所以通常对冲突进行处理。
常用的解决哈希冲突（Hash Collisions）的方法有以下几种：
开放定址法（open addressing）
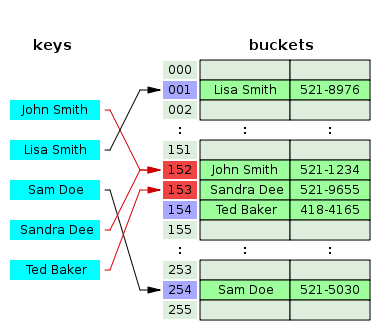
线性探查（Linear Probing）
在开放寻址法中，最简单的一种实现就是线性探查（Linear Probing），步骤如下：
- 当插入新的元素时，使用哈希函数在哈希表中定位元素位置；
- 检查哈希表中该位置是否已经存在元素。如果该位置内容为空，则插入并返回，否则转向步骤 3。
- 如果该位置为 i，则检查 i+1 是否为空，如果已被占用，则检查 i+2，依此类推（沿着地址往下探测），直到找到一个内容为空的位置。
线性探查（Linear Probing）方式虽然简单，但并不是解决冲突的最好的策略，因为它会导致同类哈希的聚集（Primary Clustering）。这导致搜索哈希表时，冲突依然存在。
二次探查（Quadratic Probing）
一种改进的方式为二次探查（Quadratic Probing），即每次检查位置空间的步长为平方倍数。也就是说，如果位置 s 被占用，则首先检查
二度哈希（Rehashing）
另一种改进的开放寻址法称为二度哈希（Rehashing），或称为双重哈希（Double Hashing）。
二度哈希的工作原理如下：
有一个包含一组哈希函数 H1…Hn 的集合。当需要从哈希表中添加或获取元素时，首先使用哈希函数 H1。如果导致冲突，则尝试使用 H2，以此类推，直到 Hn。所有的哈希函数都与 H1 十分相似，不同的是它们选用的乘法因子（multiplicative factor）。
单独链表法（Separate Chaining）
**链接技术（chaining）**将采用额外的数据结构来处理冲突，其将哈希表中每个位置（slot）都映射到了一个链表。当冲突发生时，冲突的元素将被添加到桶（bucket）列表中，而每个桶都包含了一个链表以存储相同哈希的元素。
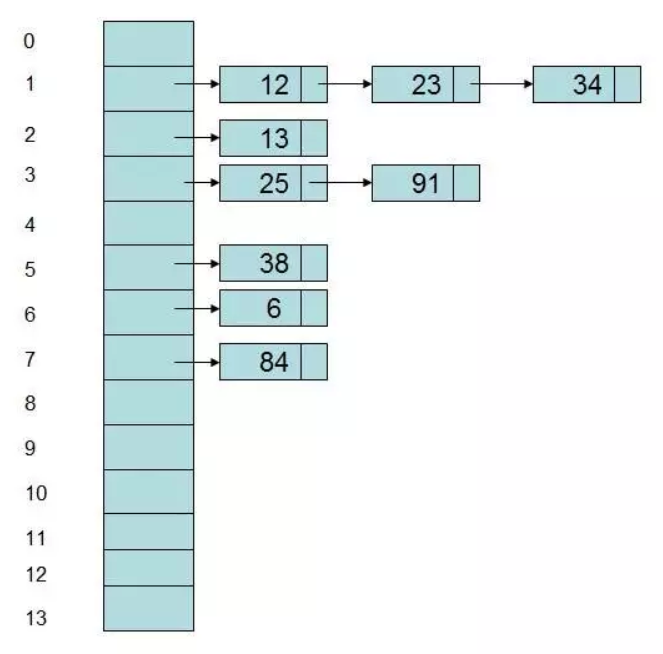
上图中的哈希表包含了 14 个桶（bucket）。如果一个新的元素要被添加至哈希表中，将会被添加至其 Key 的哈希所对应的桶中。如果在相同位置已经有一个元素存在了，则将会将新元素添加到列表的前面。
使用链接技术添加元素的操作涉及到哈希计算和链表操作，但其仍为常量，渐进时间为 O(1)。而进行查询和删除操作时，其平均时间取决于元素的数量和桶（bucket）的数量。具体的说就是运行时间为 O(n/m)，这里 n 为元素的总数量，m 是桶的数量。但通常对哈希表的实现几乎总是使 n = O(m)，也就是说，元素的总数绝不会超过桶的总数，所以 O(n/m) 也变成了常量 O(1)。
Rehash (Dynamic resizing)
很多语言或者工具包哈希表的内部实现都使用了两个数组，其中一个作为备用。如果当前哈希表的负载因子（元素个数/哈希表容量大小）过大或者过小时，就需要将数据切换到备用数组里面，这个过程就是 rehash。
新的哈希表的大小可以有很多种方案，比如 redis 里面的哈希表（字典的底层实现）扩展时，新的哈希表的大小为大于当前哈希表里面存放元素的 2 倍的最小的 2 的 n 次幂。
Rehash 过程也很有讲究，这个过程不应该影响当前系统的运行，所以比较推崇的一种方法是渐进式 rehash。渐进式 rehash 的主要思想是在 rehash 阶段对于新的写请求，并不会写入老的哈希表里面，而是直接写入到新的哈希表里；对于读请求，优先读取新的哈希表，如果不存在，则去读老的的哈希表同时将这条数据迁移到新的哈希表里面来。
Resizing by moving all entries
Generally, a new hash table with a size double that of the original hash table gets allocated privately and every item in the original hash table gets moved to the newly allocated one by computing the hash values of the items followed by the insertion operation. Rehashing is simple, but computationally expensive.
Alternatives to all-at-once rehashing
Some hash table implementations, notably in real-time systems, cannot pay the price of enlarging the hash table all at once, because it may interrupt time-critical operations. If one cannot avoid dynamic resizing, a solution is to perform the resizing gradually to avoid storage blip—typically at 50% of new table’s size—during rehashing and to avoid memory fragmentation that triggers heap compaction due to deallocation of large memory blocks caused by the old hash table. In such case, the rehashing operation is done incrementally through extending prior memory block allocated for the old hash table such that the buckets of the hash table remain unaltered.
Rehash 有一个问题需要讨论一下：如何鉴定 rehash 阶段的开始与结束？开始很简单，每次写操作或者定期检测一下负载因子，当满足条件则开始 rehash。那么如何鉴定结束呢？一种比较常规的方法是定期检测，但是这涉及到很多问题，比如如何界定检测的时间粒度。另一种是记录下迁移过程。还是以 Redis 为例来说明，Redis 使用的是哈希表元素作为链表头不存储元素的方式，这样数据迁移的时候只需要从原链表将节点删除，然后插入到新的哈希表对应的位置就好了。同时哈希表结构有一个字段记录了老的哈希表残留的数据，这样我们只需要检测这个变量（代价很小）就知道 rehash 有没有完成了。
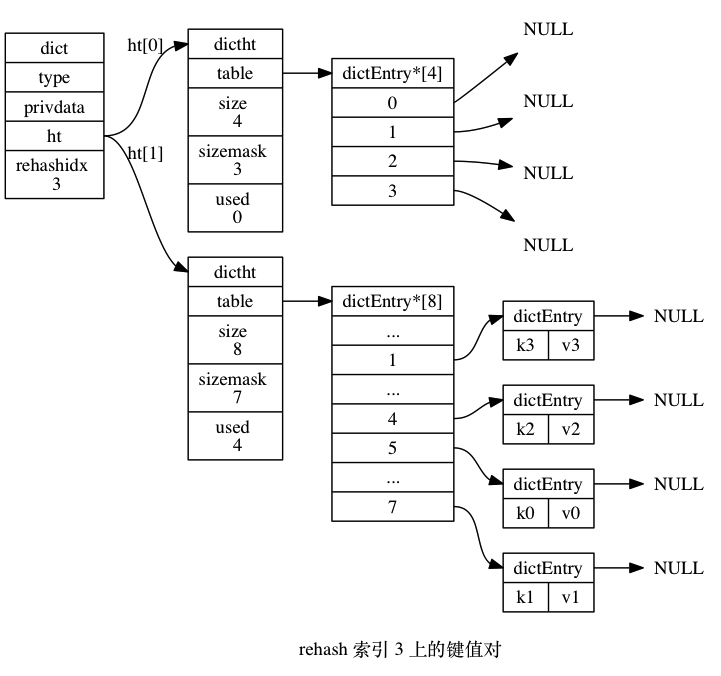
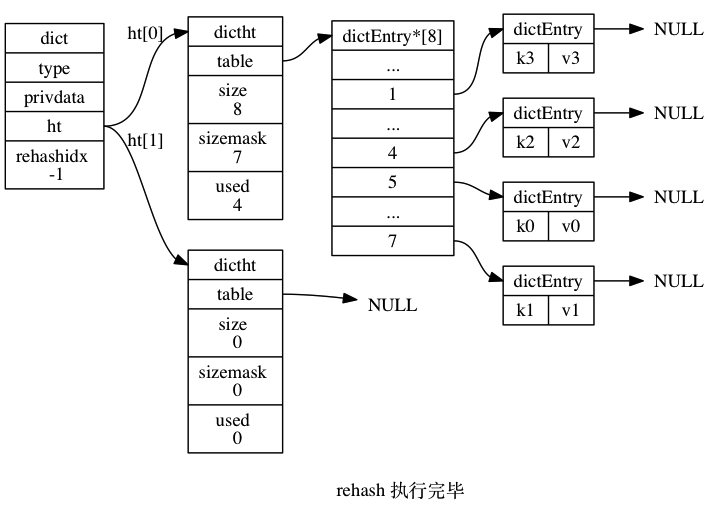
rehash 过程如下图所示（来自 《Redis 设计与实现》）：
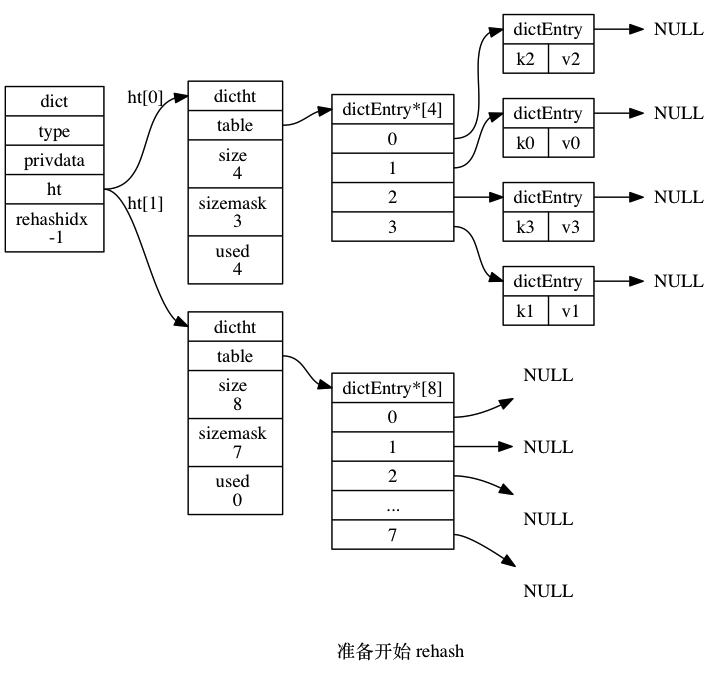
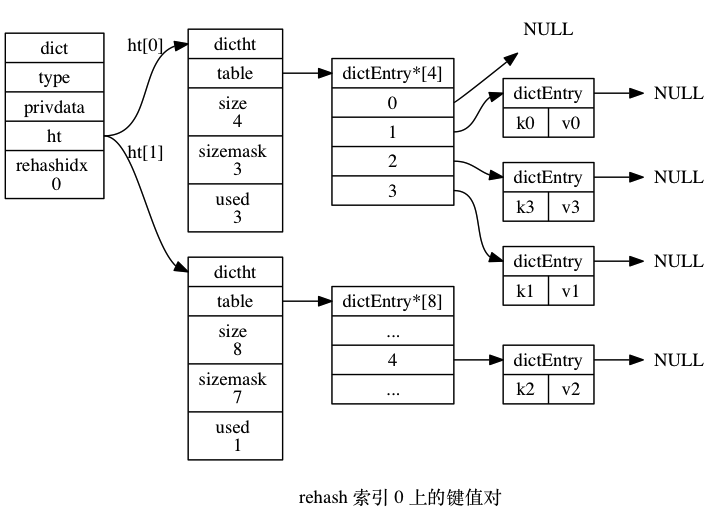
迁移索引 1 和 2 上的过程图略去。
