线性表（Linear List）
基本概念
线性表（List）：由零个或多个数据元素组成的有限序列。
- 线性表是一个序列。
- 0个元素构成的线性表是空表。
- 线性表中的第一个元素无前驱，最后一个元素无后继，其他元素有且只有一个前驱和后继。
- 线性表是有长度的，其长度就是元素个数，且线性表的元素个数是有限的，也就是说，线性表的长度是有限的。
如果用数学语言来进行定义，可如下：
若将线性表记为（a1,…,ai-1,ai,ai+1,…an）,则表中ai-1领先于ai,ai领先于ai+1,称ai-1是ai的直接前驱元素,ai+1是ai的直接后继元素。
数组，链表、队列、栈等都是线性表结构。
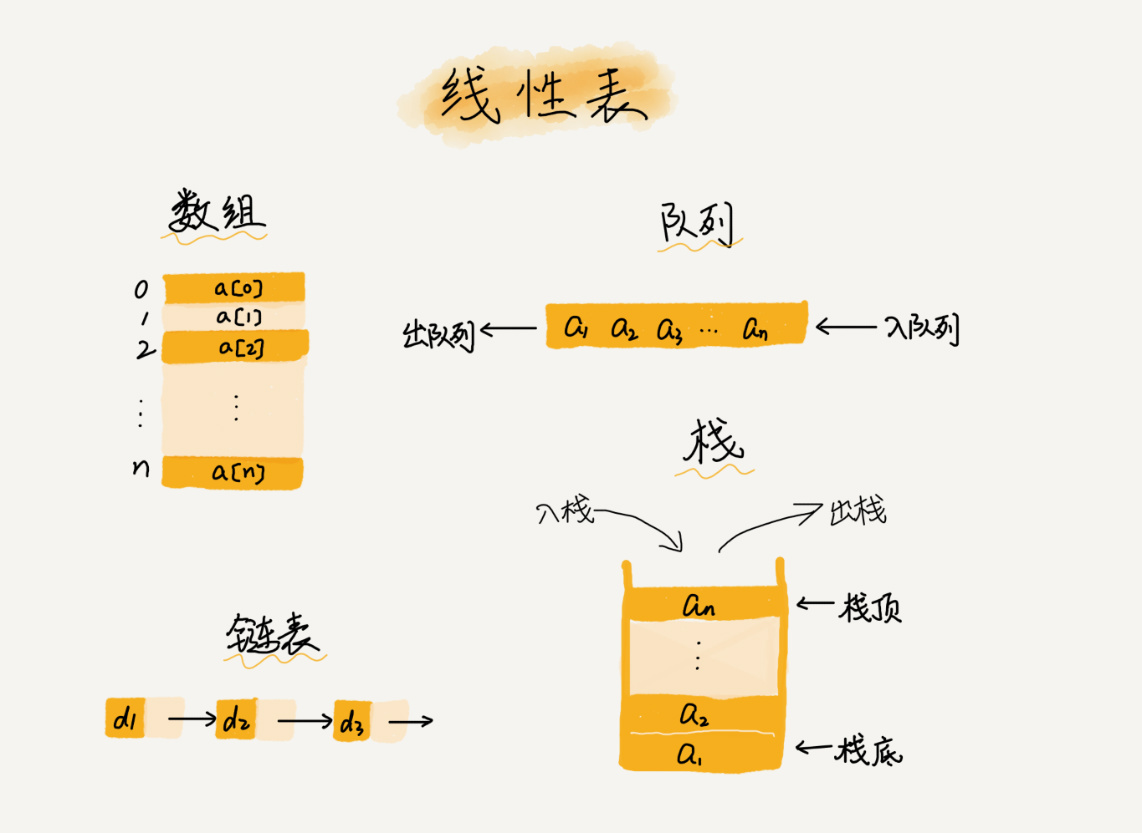
而与它相对立的概念是非线性表，比如二叉树、堆、图等。之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系。
特殊的线性表 - 栈（Stack）和队列（Queue）
栈和队列是两种比较特殊的线性表。
栈（Stack）
栈是一种操作受限制的线性表。其限制是仅允许在线性表的尾部进行添加和删除操作，这一端被称为栈顶，另一端称为栈底。向一个栈添加新元素叫压栈（push），删除元素又称为出栈（pop）。
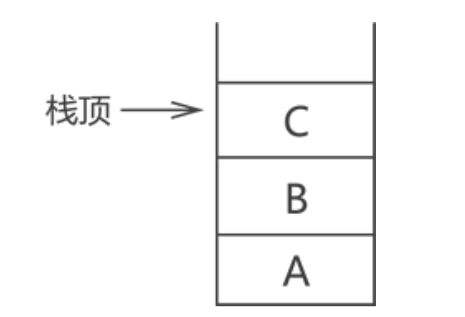
栈结构如上图所示，像一个木桶，栈中含有 3 个元素，分别是 A、B 和 C，从在栈中的状态可以看出 A 最先进的栈，然后 B 进栈，最后 C 进栈。根据“先进后出”的原则，3 个元素出栈的顺序应该是：C 最先出栈，然后 B 出栈，最后才是 A 出栈。
队列（Queue）
队列也是一种操作受限制的线性表。
队列中的元素只能从线性表的一端进，从另一端出，且要遵循“先入先出”的特点，即先进队列的元素也要先出队列。
队列结构如上图所示，队列中有 3 个元素，分别是 A、B 和 C，从在队列中的状态可以看出是 A 先进队列，然后 B 进，最后 C 进。根据“先进先出”的原则，3 个元素出队列的顺序应该是 A 最先出队列，然后 B 出，最后 C 出。
线性表（Linear List）的物理结构
逻辑结构（logical structure）和物理结构（physical structure）
我们知道，数据结构分为逻辑结构（logical structure）和物理结构（physical structure），
- **逻辑结构（logical structure）**分为集合结构、线性结构、树形结构和图形结构四大类。
- **物理结构（physical structure）**分为顺序存储结构（sequence storage structure）和链式存储结构（linked storage structure）。
线性表（Linear List）的物理结构
线性表（Linear List）是线性结构的一种，那么线性表当然也有物理结构。
从下图中，我们可以看出，线性表存储数据的方式（线性表（Linear List）的物理结构）可分为以下 2 种：
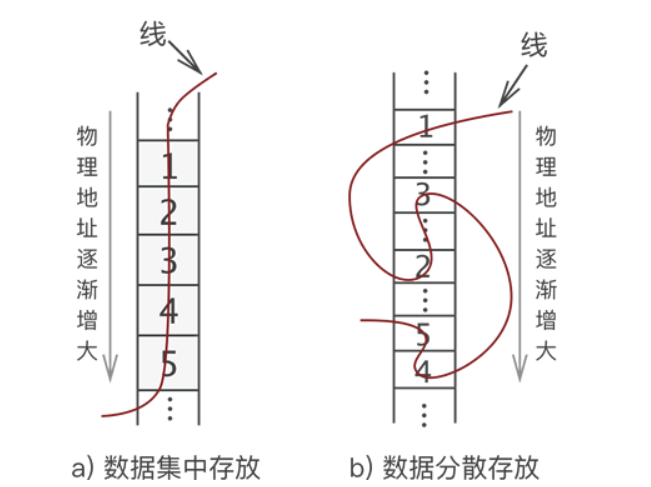
- 如图中 a) 所示，将数据依次存储在连续的整块物理空间中，这种存储结构称为顺序存储结构（简称顺序表，linear list）；
- 如图中 b) 所示，数据分散的存储在物理空间中，通过一根线保存着它们之间的逻辑关系，这种存储结构称为链式存储结构（简称链表，linked list）；
前驱和后继
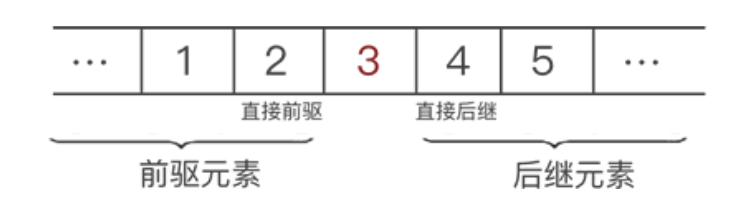
数据结构中，一组数据中的每个个体被称为“数据元素”（简称“元素”）。例如，下图显示的这组数据，其中 1、2、3、4 和 5 都是这组数据组的一个元素。
另外，对于具有“一对一”逻辑关系的数据，我们一直在用“某一元素的左侧（前边）或右侧（后边）”这样不专业的词，其实线性表中有更准确的术语：
- 某一元素的左侧相邻元素称为“直接前驱”，位于此元素左侧的所有元素都统称为“前驱元素”；
- 某一元素的右侧相邻元素称为“直接后继”，位于此元素右侧的所有元素都统称为“后继元素”；
以下图数据中的元素 3 来说，它的直接前驱是 2 ，此元素的前驱元素有 2 个，分别是 1 和 2；同理，此元素的直接后继是 4 ，后继元素也有 2 个，分别是 4 和 5。
顺序表（Sequence List）- 顺序存储结构的线性表
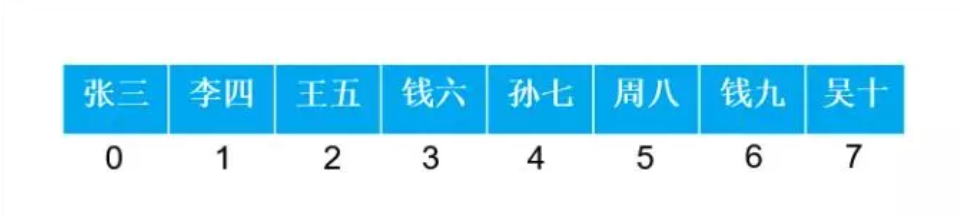
顺序表（Sequence List）是指顺序存储结构的线性表，指的是用一段地址连续的存储单元依次存储线性表的数据元素。
顺序表表现在物理内存中，也就是物理上的存储方式，事实上就是在内存中找个初始地址，然后通过占位的形式，把一定的内存空间给占了，然后把相同数据类型的数据元素依次放在这块空地中。注意，这块物理内存的地址空间是连续的。
顺序表（Sequence List）的存储结构如下图：
顺序表优缺点
线性表的顺序存储结构，在存、读取数据时，不管是在哪个位置，时间复杂度都是O(1)。而在插入或者删除时，时间复杂度都是O(n)。 这也就是线性表的顺序存储结构比较适合存取数据，不适合经常插入和删除数据的应用。
优点
- 无需为了表示表中元素之间的逻辑关系而增加额外的存储空间（相对于链式存储而言）。
- 可以快速的存取表中任意位置的元素。
缺点
- 插入和删除操作需要移动大量的元素。
- 当线性表长度变化较大时，难以确定存储空间的容量。
- 容易造成存储空间的“碎片”(因为线性表的顺序存储结构申请的内存空间都以连续的，如果因为某些操作（比如删除操作）导致某个部分出现了一小块的不连续内存空间，因为这一小块内存空间太小不能够再次被利用/分配，那么就造成了内存浪费，也就是“碎片”)
链表（Linked List）- 链式存储结构的线性表
背景
前面我们讲的线性表的顺序存储结构，它最大的缺点就是插入和删除时需要移动大量元素，这显然就需要耗费时间。
那我们能不能针对这个缺陷或者说遗憾提出解决的方法呢？要解决这个问题，我们就得考虑一下导致这个问题的原因！为什么当插入和删除时，就要移动大量的元素？
原因就在于相邻两元素的存储位置也具有邻居关系，它们在内存中的位置是紧挨着的，中间没有间隙，当然就无法快速插入和删除。
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以存在内存中未被占用的任意位置。
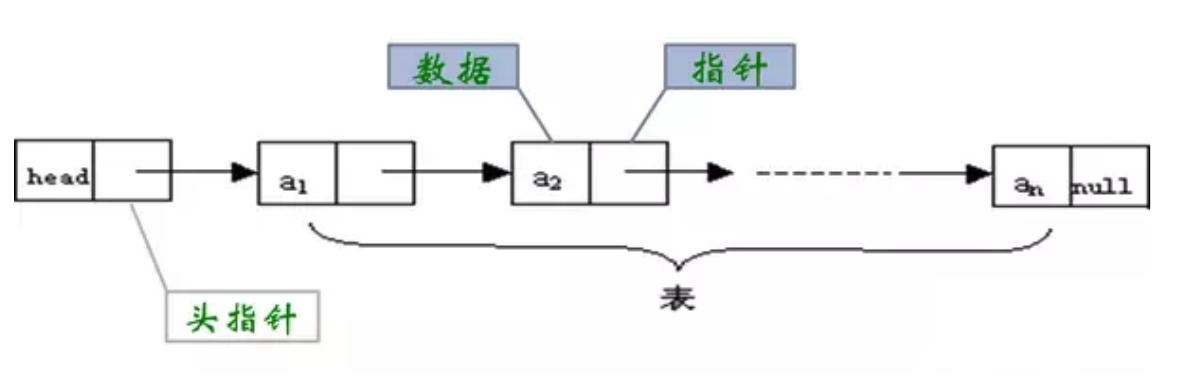
也就是说，链式存储结构的线性表由一个或者多个结点（Node）组成。每个节点内部又分为数据域和指针域（链）。数据域存储了数据元素的信息。指针域存储了当前结点指向的直接后继的指针地址。
因为每个结点只包含一个指针域，所以叫做单链表。顾名思义，当然还有双链表。
单向链表（Singly Linked List）
单向链表（Singly Linked List）很简单，其在内存中的对象是随机分布的，对象不但存储了一个数据域，还包括一个指针域，指向下一个对象，来确定一组对象的逻辑顺序。
循环链表（Circular Linked List）
循环链表（Circular Linked List）也很简单，和单向链表类似，唯一的区别是，只不过循环链表的最后一个对象的next又指向了第一个对象。
双向链表（Doubly Linked List）
不但持有next引用，指向下一个对象，还持有一个prev引用，指向上一个对象。
记住双向链表这个图，很重要，下一篇文章我们要讲的LinkedList就是以双向链表的方式实现的。
Reference
- Java数据结构之线性表-Java那些事儿专栏 - https://juejin.im/post/5a7458925188257a6049699c
- 数据结构与算法之线性表 - https://www.jianshu.com/p/1174663be688
- 数据结构概述 - http://data.biancheng.net/intro/
- https://time.geekbang.org/column/article/40961