链表(Linked List)
链表(Linked List),别名链式存储结构或单链表,用于存储逻辑关系为 “一对一” 的数据。与顺序表不同,链表不限制数据的物理存储状态,换句话说,使用链表存储的数据元素,其物理存储位置是随机的。
例如,使用链表存储 {1,2,3},数据的物理存储状态如下图所示:
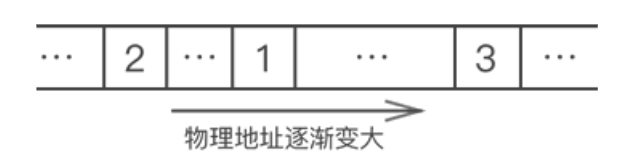
我们看到,上图根本无法体现出各数据之间的逻辑关系。对此,链表的解决方案是,每个数据元素在存储时都配备一个指针,用于指向自己的直接后继元素。如下图所示:
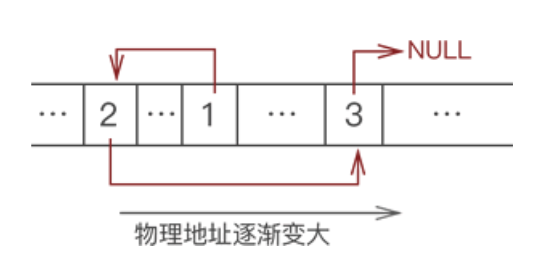
像上图这样,数据元素随机存储,并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。
也就是说:链表具有动态的能力,不需要去处理固定容量的问题
正因为链表具备这种动态能力,那它也就缺失了**高效的random access(随机访问)**的能力。它无法与数组一样,通过一个索引(index)直接获取对应的元素。
因为在底层机制中数组开辟的空间在内存中是连续分布的,我们可以直接寻找索引对应的偏移,直接计算出数据所存储的内存地址,直接用O(1)复杂度拿出。
链表靠next连接,每个节点存储地址不同,我们只能通过next顺藤摸瓜找到我们要找的元素。
链表的节点
链表中每个数据的存储都由以下两部分组成:
- 数据元素本身,其所在的区域称为数据域(data field);
- 指向直接后继元素的指针,所在的区域称为指针域(pointer field);
即链表中存储各数据元素的结构如下图所示:

上图所示的结构在链表中称为节点。也就是说,链表实际存储的是一个一个的节点,真正的数据元素包含在这些节点中,如下图所示:
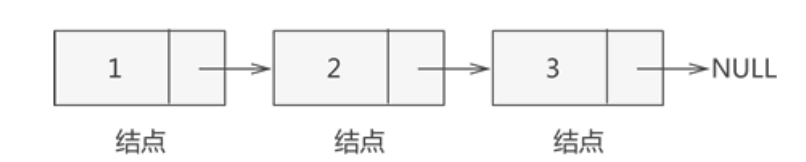
因此,链表中每个节点的具体实现,需要使用 C 语言中的结构体,具体实现代码为:
typedef struct Link{
char elem; //代表数据域
struct Link * next; //代表指针域,指向直接后继元素
}link; //link为节点名,每个节点都是一个 link 结构体
提示,由于指针域中的指针要指向的也是一个节点,因此要声明为 Link 类型。
头节点,头指针和首元节点
其实,上图所示的链表结构并不完整。一个完整的链表需要由以下几部分构成:
- 头指针:一个普通的指针,它的特点是永远指向链表第一个节点的位置。很明显,头指针用于指明链表的位置,便于后期找到链表并使用表中的数据;
- 节点:链表中的节点又细分为头节点、首元节点和其他节点:
- 头节点:其实就是一个不存任何数据的空节点,通常作为链表的第一个节点。对于链表来说,头节点不是必须的,它的作用只是为了方便解决某些实际问题;
- 首元节点:由于头节点(也就是空节点)的缘故,链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓,没有实际意义;
- 其他节点:链表中其他的节点;
因此,一个存储 {1,2,3} 的完整链表结构如下图所示:
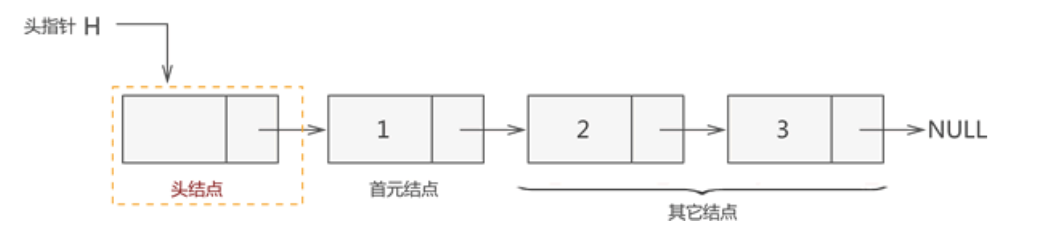
注意:链表中有头节点时,头指针指向头节点;反之,若链表中没有头节点,则头指针指向首元节点。
性能
| 接口 | 说明 | 时间复杂度 |
|---|---|---|
| add(index, e) | 插入操作 | O(n) |
| remove(index, e) | 删除操作 | O(n) |
| set(index, e) | 修改操作 | O(n) |
| get(index, e) | 查找操作 | O(n) |
| contains(index, e) | 也是查找操作 | O(n) |
正因为链表没有索引,因此链表丧失了像数组那样快速访问的能力,这也就让链表的增删改查全都是O(n)级别的。
由于链表不需要像数组一下子必须new出来一片空间,因而需要多少个数据,就生成多少个节点挂接起来,最终不存在空间浪费的问题。换句话说,链表具有动态的能力,不需要去处理固定容量的问题。
正因为链表具备这种动态能力,那它也就缺失了**高效的random access(随机访问)**的能力。它无法与数组一样,通过一个索引(index)直接获取对应的元素。
因为从底层实现来说,数组开辟的空间在内存中是连续分布的,因此我们就可以计算出该索引对应的偏移量(offset),进而计算出数据所存储的内存地址,直接用O(1)复杂度拿出。
而链表靠next连接,每个节点的存储地址不同,因此我们只能通过 next 域不断“顺藤摸瓜”找到我们要找的元素。
从上表的时间复杂度来看,这似乎说明链表是一个性能不太优的数据结构,我们来对链表的接口进行一些调整,然后在看一下 时间复杂度 。
| 接口 | 说明 | 复杂度 |
|---|---|---|
| addFirst(index, e) | 插入表头操作 | O(1) |
| addLast(index, e) | 插入链尾操作 | O(1) |
| removeFirst(index, e) | 删除表头操作 | O(1) |
| removeLast(index, e) | 删除链尾操作 | O(1) |
| getFirst(index, e) | 查找链表头操作 | O(1) |
经过添加这些接口,链表的在使用时复杂度就变成了O(1)。
链表的创建(初始化)
我们只需在主函数中调用 initLink 函数,即可轻松创建一个存储 {1,2,3,4} 的链表,C 语言完整代码如下:
#include <stdio.h>
#include <stdlib.h>
//链表中节点的结构
typedef struct Link{
int elem;
struct Link *next;
}link;
//初始化链表的函数
link * initLink();
//用于输出链表的函数
void display(link *p);
int main() {
//初始化链表(1,2,3,4)
printf("初始化链表为:\n");
link *p=initLink();
display(p);
return 0;
}
link * initLink(){
link * p=NULL;//创建头指针
link * temp = (link*)malloc(sizeof(link));//创建首元节点
//首元节点先初始化
temp->elem = 1;
temp->next = NULL;
p = temp;//头指针指向首元节点
for (int i=2; i<5; i++) {
link *a=(link*)malloc(sizeof(link));
a->elem=i;
a->next=NULL;
temp->next=a;
temp=temp->next;
}
return p;
}
void display(link *p){
link* temp=p;//将temp指针重新指向头结点
//只要temp指针指向的结点的next不是Null,就执行输出语句。
while (temp) {
printf("%d ",temp->elem);
temp=temp->next;
}
printf("\n");
}
程序运行结果为:
初始化链表为:
1 2 3 4
链表的基本操作
本节将详细介绍对链表的一些基本操作,包括对链表中数据的添加、删除、查找(遍历)和更改。
注意,以下对链表的操作实现均建立在已创建好链表的基础上,创建链表的代码如下所示:
//声明节点结构
typedef struct Link{
int elem;//存储整形元素
struct Link *next;//指向直接后继元素的指针
}link;
//创建链表的函数
link * initLink(){
link * p=(link*)malloc(sizeof(link));//创建一个头结点
link * temp=p;//声明一个指针指向头结点,用于遍历链表
//生成链表
for (int i=1; i<5; i++) {
//创建节点并初始化
link *a=(link*)malloc(sizeof(link));
a->elem=i;
a->next=NULL;
//建立新节点与直接前驱节点的逻辑关系
temp->next=a;
temp=temp->next;
}
return p;
}
从实现代码中可以看到,该链表是一个具有头节点的链表。由于头节点本身不用于存储数据,因此在实现对链表中数据的"增删查改"时要引起注意。
链表插入元素
同顺序表一样,向链表中增添元素,根据添加位置不同,可分为以下 3 种情况:
- 插入到链表的头部(头节点之后),作为首元节点;
- 插入到链表中间的某个位置;
- 插入到链表的最末端,作为链表中最后一个数据元素;
思想
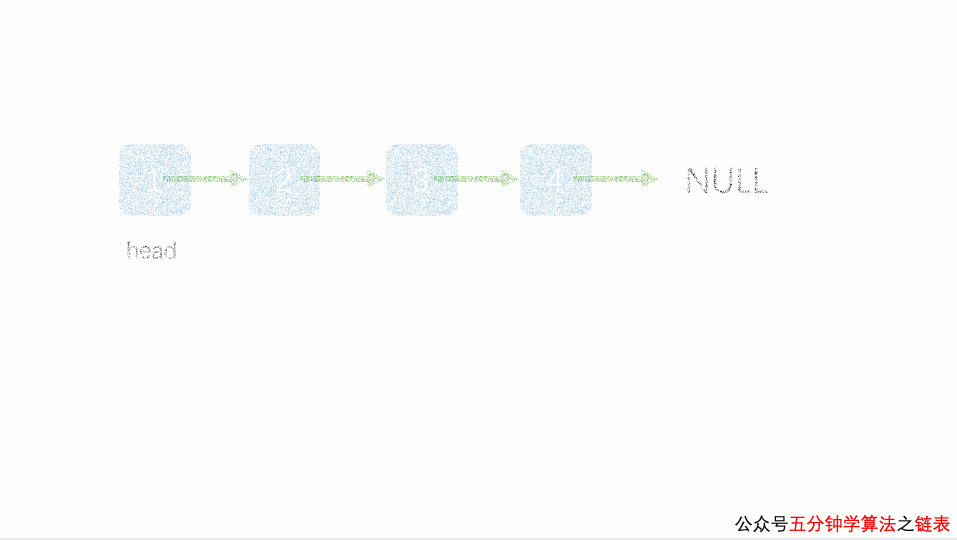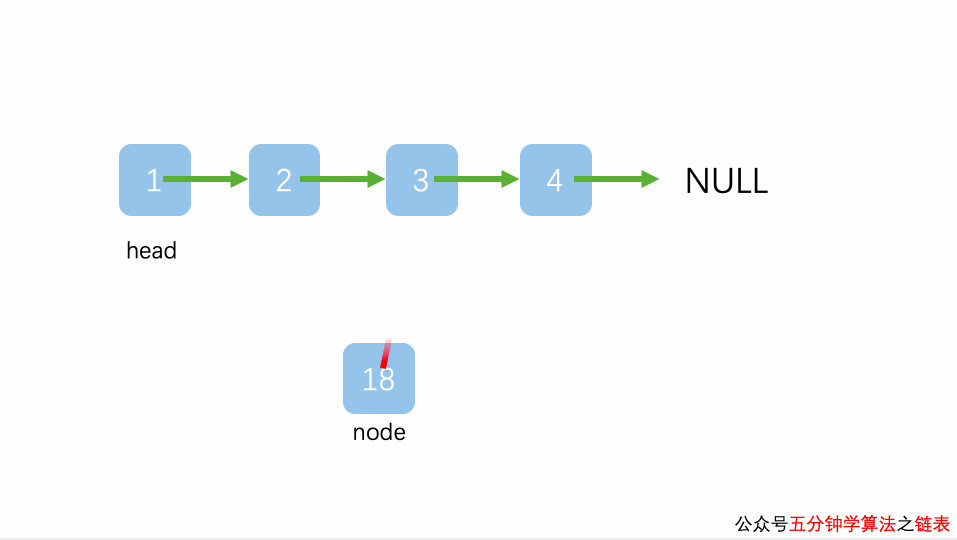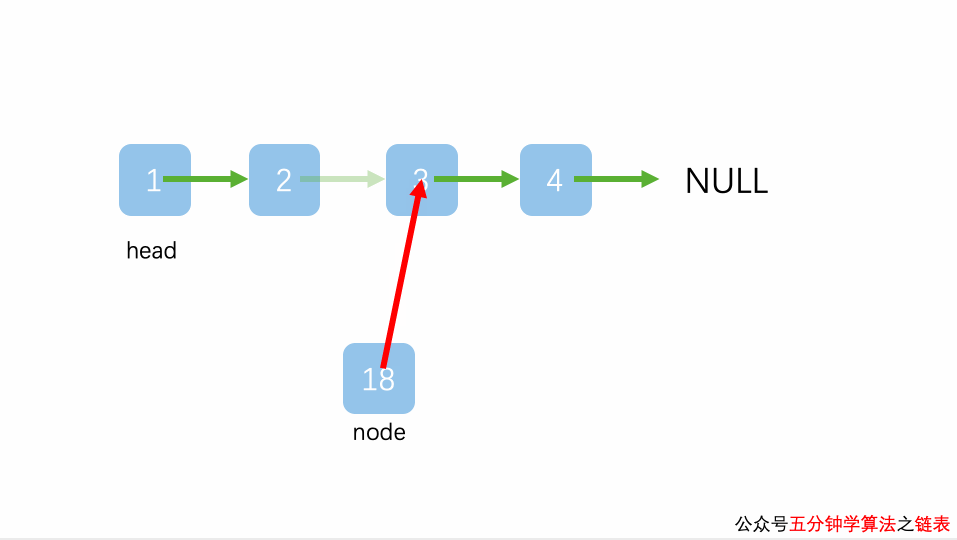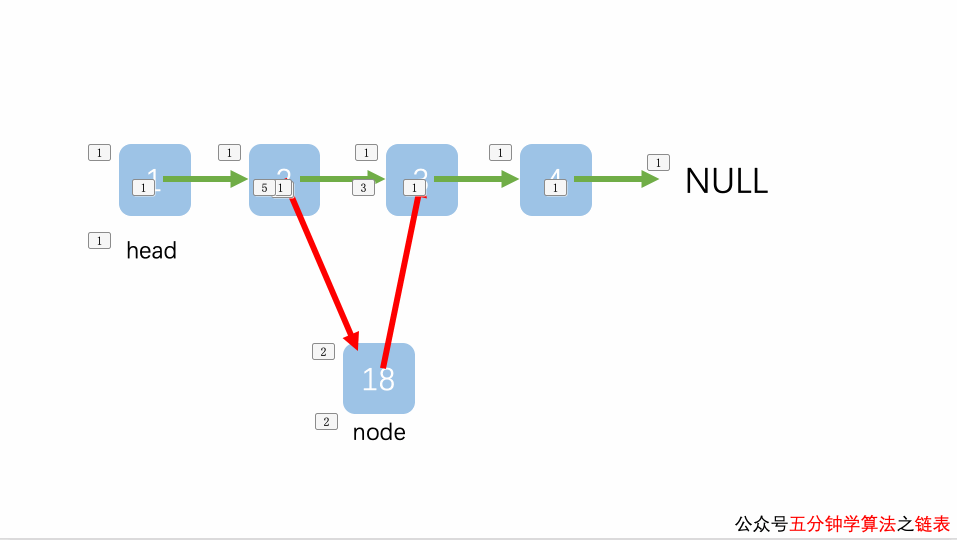
虽然新元素的插入位置不固定,但是链表插入元素的思想是固定的,只需做以下两步操作,即可将新元素插入到指定的位置:
- 将新结点的 next 指针指向插入位置后的结点;
- 将插入位置前结点的 next 指针指向插入结点;
例如,我们在链表 {1,2,3,4} 的基础上分别实现在头部、中间部位、尾部插入新元素 5,其实现过程如下图所示:
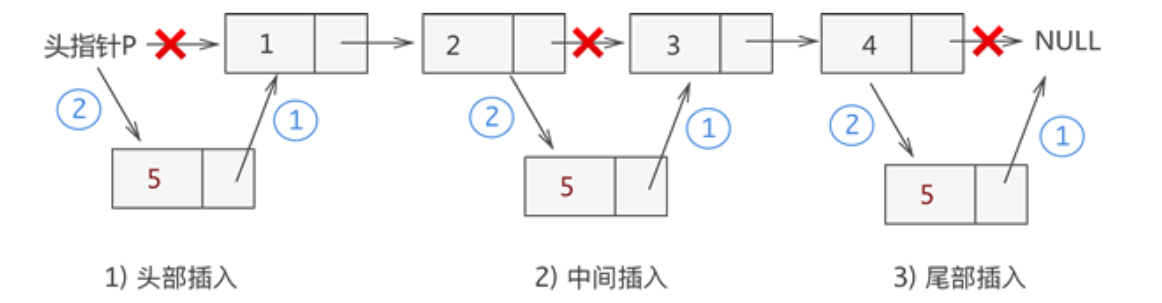
从图中可以看出,虽然新元素的插入位置不同,但实现插入操作的方法是一致的,都是先执行步骤 1 ,再执行步骤 2。
三种插入情况
插入到链表的头部(头节点之后)
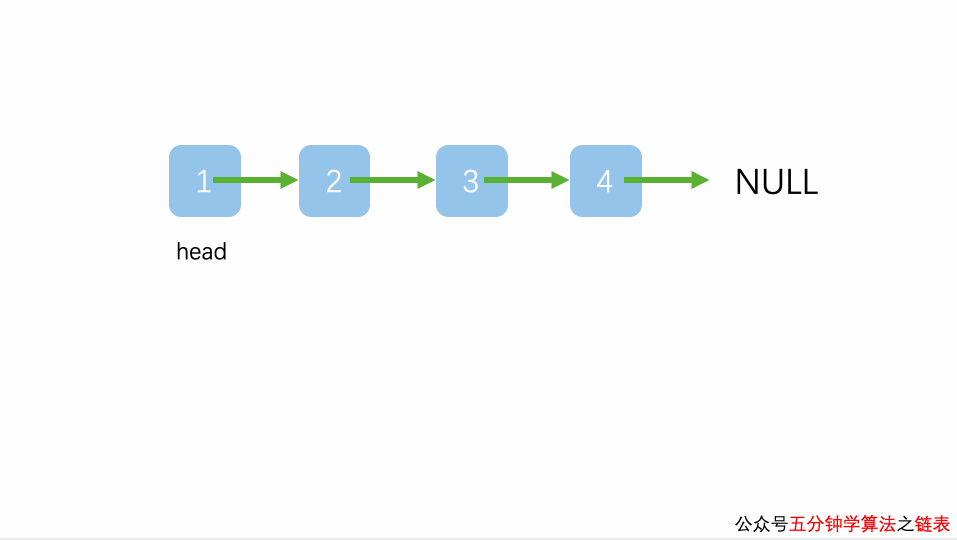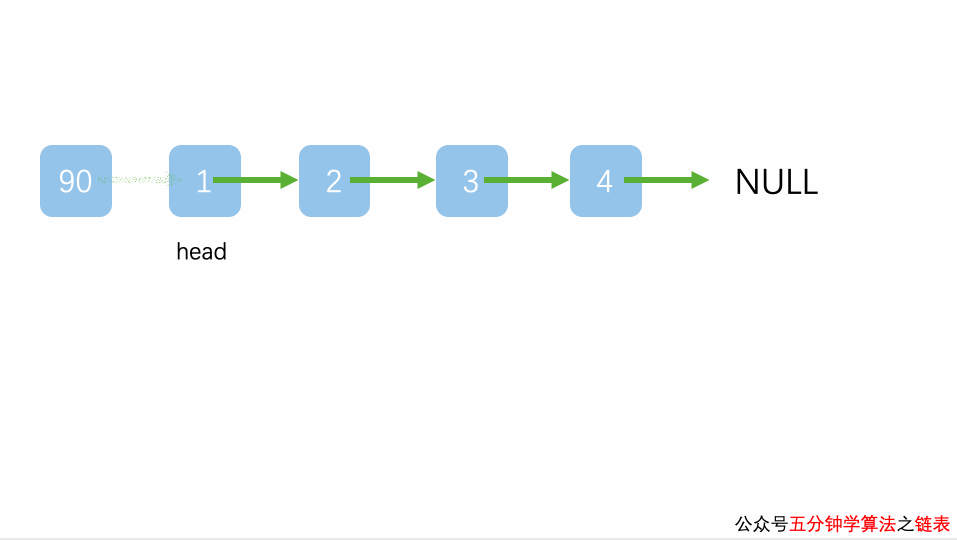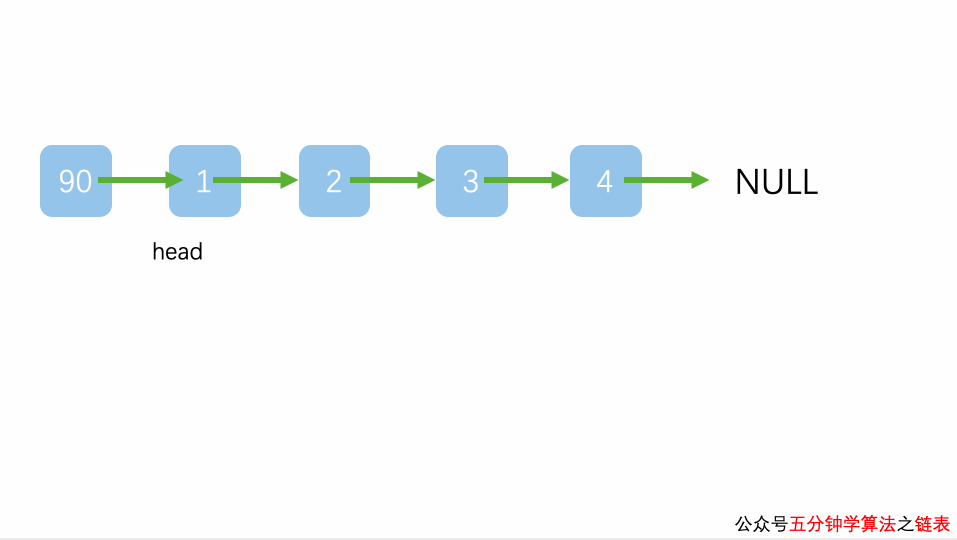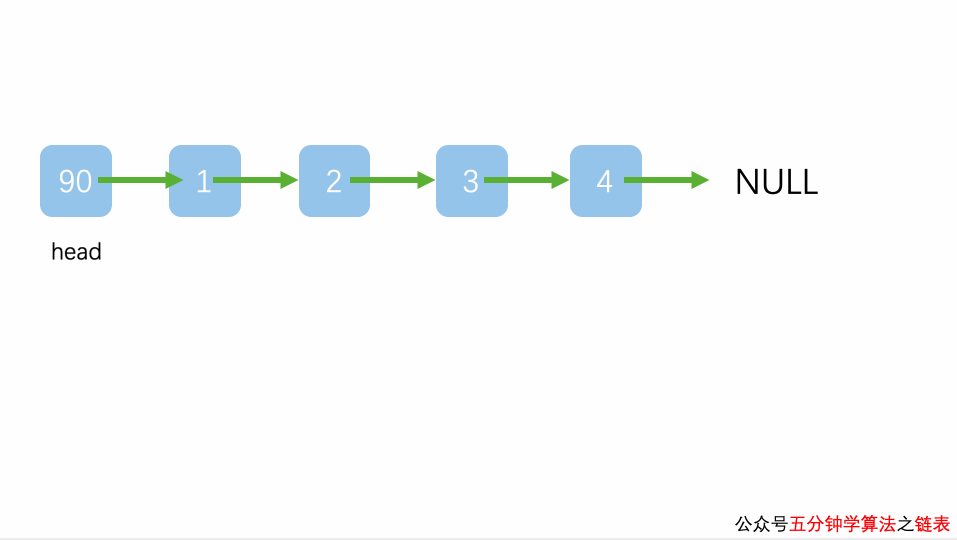
插入到链表中间的某个位置
插入到链表的最末端
“插入到链表的最末端”的情况其实和“插入到链表中间的某个位置”的相同的,唯一有一个微小的不同是 pre.next 为 null,而 pre.next 为 null并不影响将 pre.next 赋值给 node.next 操作(只不过 node.next 最终值为 null 罢了)。
虚拟的头结点(Dummy)
值得注意的是,在前面总结的向链表插入元素的步骤 2 中(将插入位置前结点的 next 指针指向插入结点)。这意味着,要向索引为 i 的位置(头部元素索引为 0)插入一个元素,我们需要先找到索引为 i-1的节点。问题就来了,如果希望在索引为0的位置(也就是链表的头部位置)插入一个元素,我们就需要先找到索引为 -1 的节点,显然这个节点是不存在的。
因此,处理链表的插入头部和插入中间的操作的代码逻辑是不一样的,那能否用同样的代码来覆盖这两种情况呢?
答案是肯定的!既然头部元素没有前驱元素,那我们就给它一个号了,因此只需要引入虚拟的头结点的概念就行了。
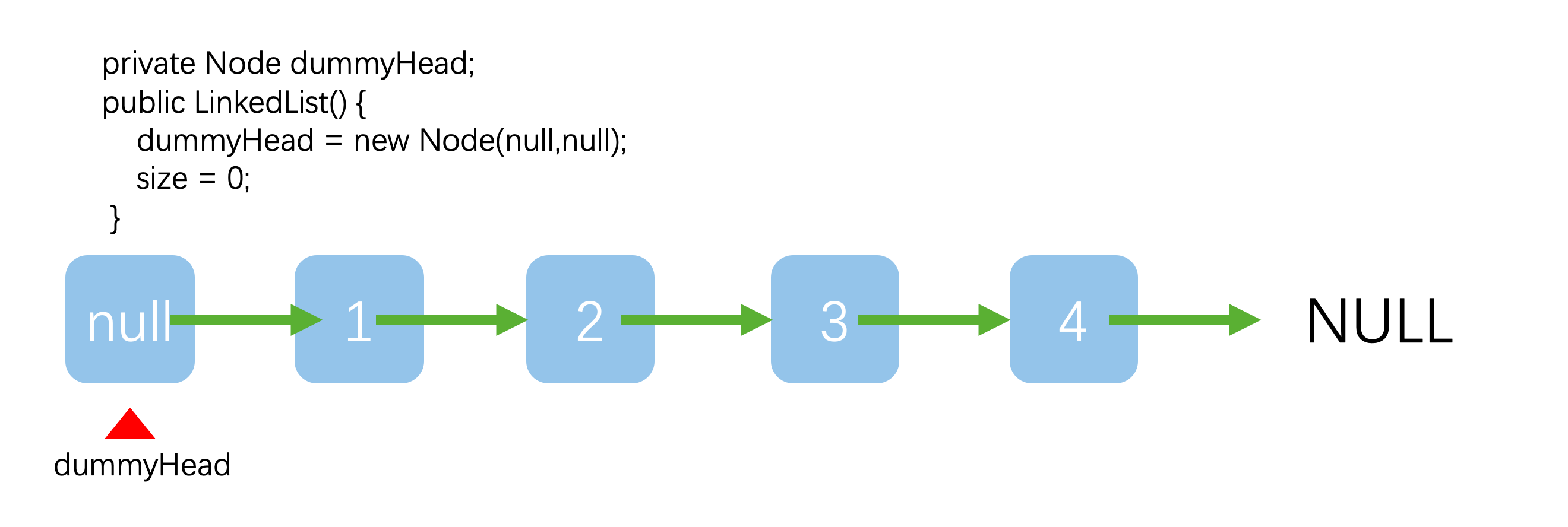
链表删除元素
从链表中删除指定数据元素时,实则就是将存有该数据元素的节点从链表中摘除,但作为一名合格的程序员,要对存储空间负责,对不再利用的存储空间要及时释放。因此,从链表中删除数据元素需要进行以下 2 步操作:
- 找到待删除元素的前驱节点
- 将待删除元素的 next 域赋值给该前驱节点的 next 域
这相当于进行下面的操作:
temp->next = temp->next->next;
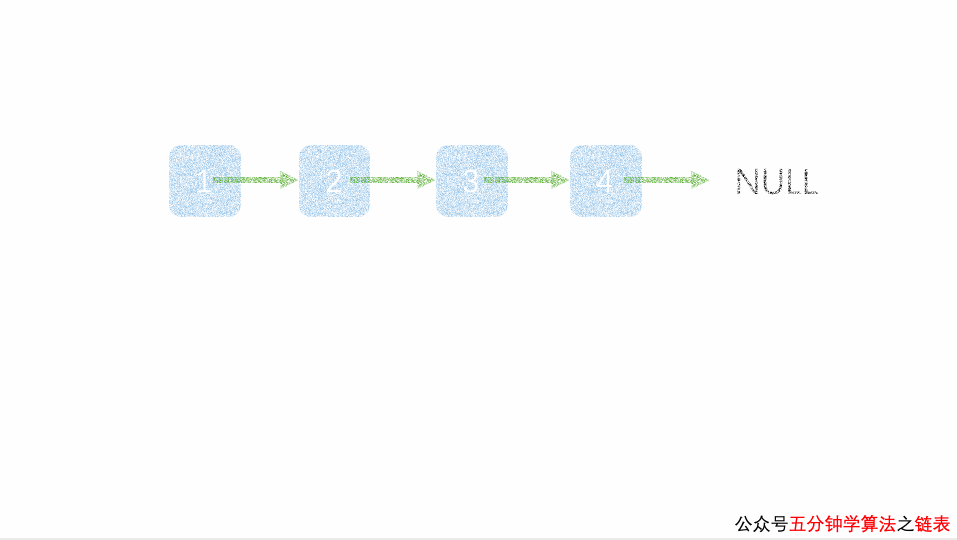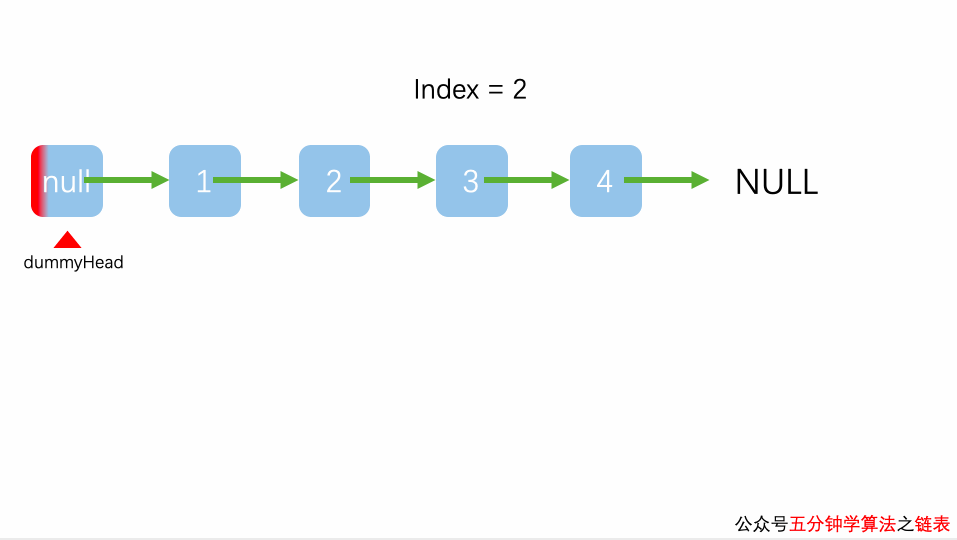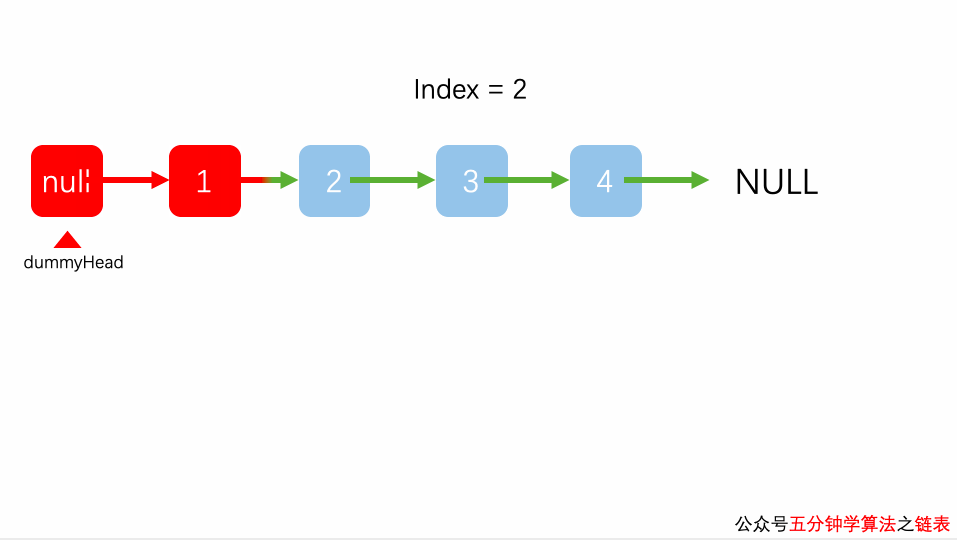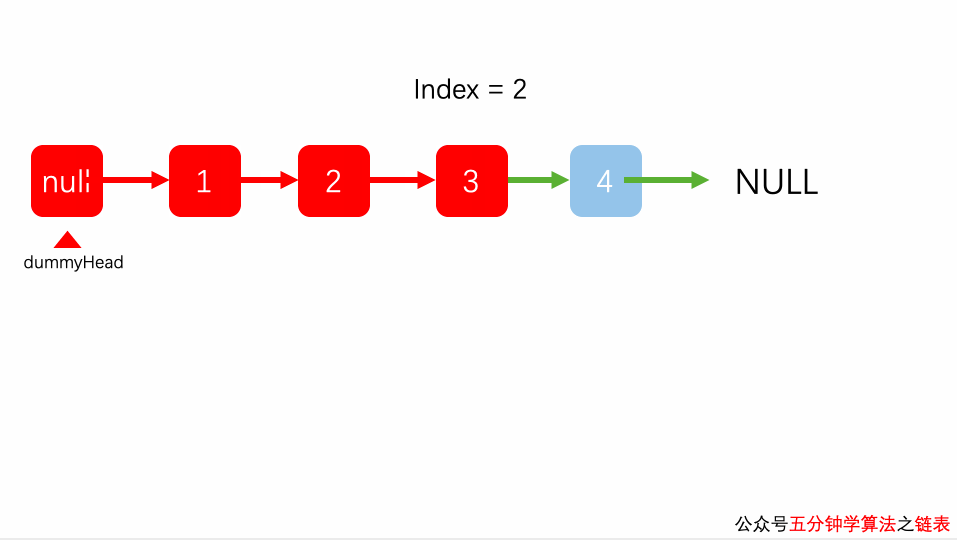
例如,从存有 {1,2,3,4} 的链表中删除元素 3,则此代码的执行效果如下图所示:

动画:

链表查找元素
在链表中查找指定数据元素,最常用的方法是:从表头依次遍历表中节点,用被查找元素与各节点数据域中存储的数据元素进行比对,直至比对成功或遍历至链表最末端的 NULL ,(比对失败的标志)。
因此,链表中查找特定数据元素的 C 语言实现代码为:
//p为原链表,elem表示被查找元素、
int selectElem(link * p,int elem){
//新建一个指针t,初始化为头指针 p
link * t=p;
int i=1;
//由于头节点的存在,因此while中的判断为t->next
while (t->next) {
t=t->next;
if (t->elem==elem) {
return i;
}
i++;
}
//程序执行至此处,表示查找失败
return -1;
}
注意,遍历有头节点的链表时,需避免头节点对测试数据的影响,因此在遍历链表时,建立使用上面代码中的遍历方法,直接越过头节点对链表进行有效遍历。
动画:
链表更新元素
更新链表中的元素,只需通过遍历找到存储此元素的节点,对节点中的数据域做更改操作即可。
直接给出链表中更新数据元素的 C 语言实现代码:
//更新函数,其中,add 表示更改结点在链表中的位置,newElem 为新的数据域的值
link *amendElem(link * p,int add,int newElem){
link * temp=p;
temp=temp->next;//在遍历之前,temp指向首元结点
//遍历到被删除结点
for (int i=1; i<add; i++) {
temp=temp->next;
}
temp->elem=newElem;
return p;
}
通过链表实现不同数据结构
链表实现栈
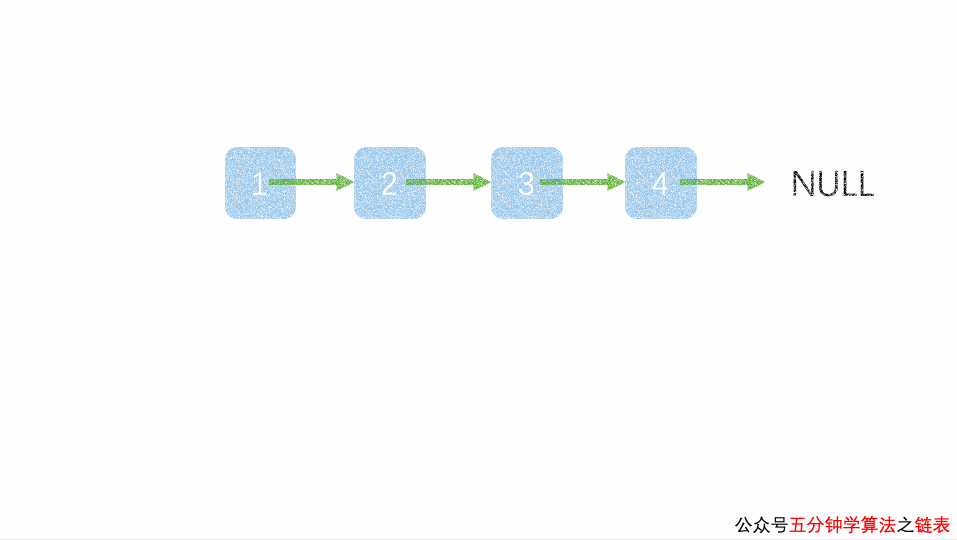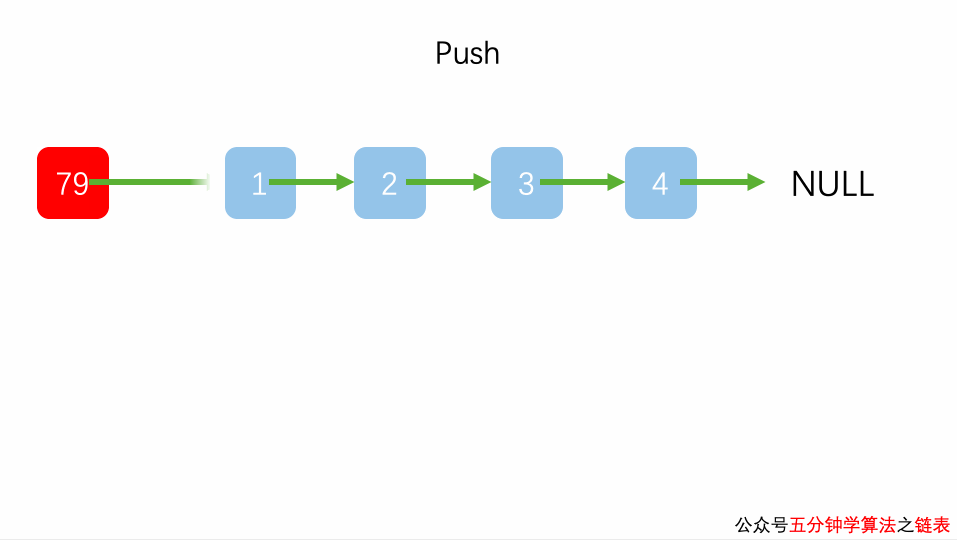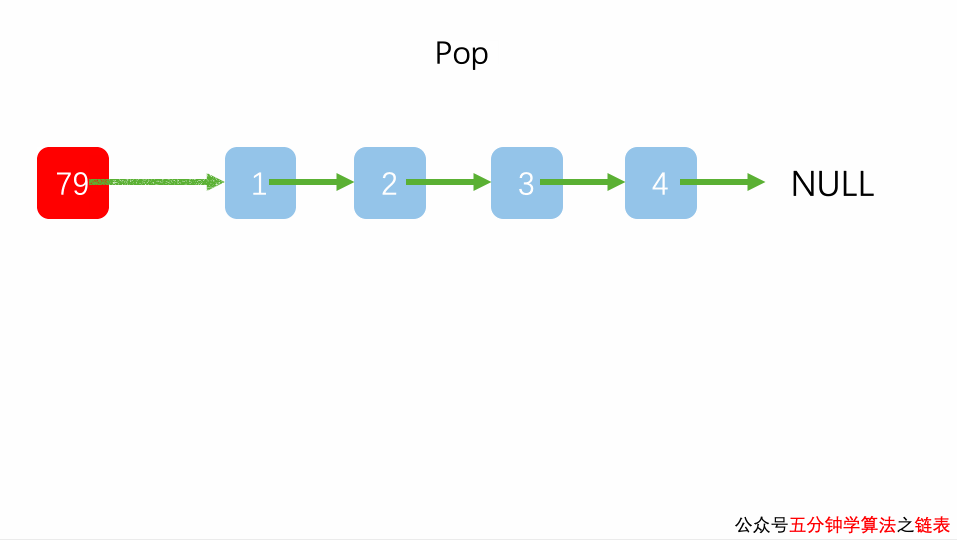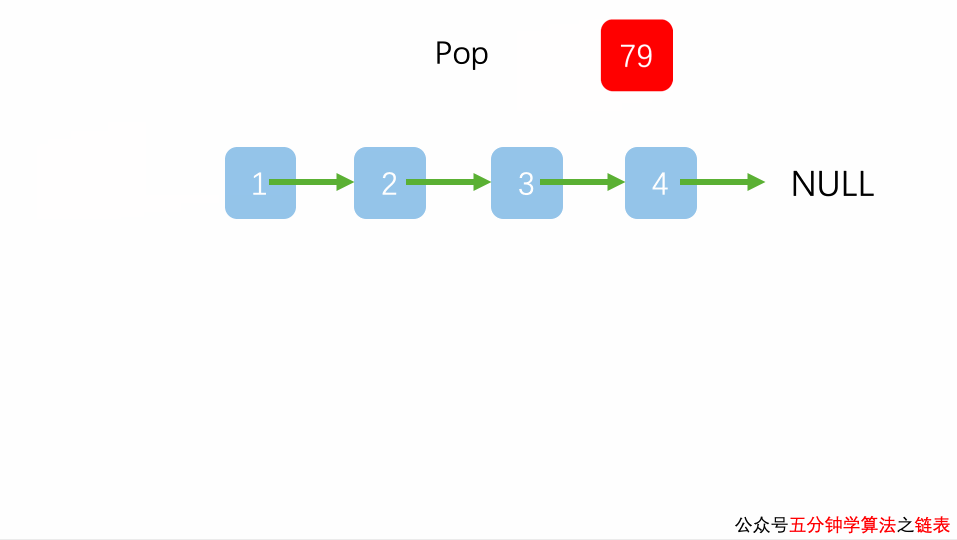
链表实现队列
根据队列的性质,对于队列的操作势必会影响到链表的两端,根据链表的时间复杂度分析,我们可以知道对队头操作的时间复杂度为O(1),而对队尾操作的时间复杂度为O(n)。
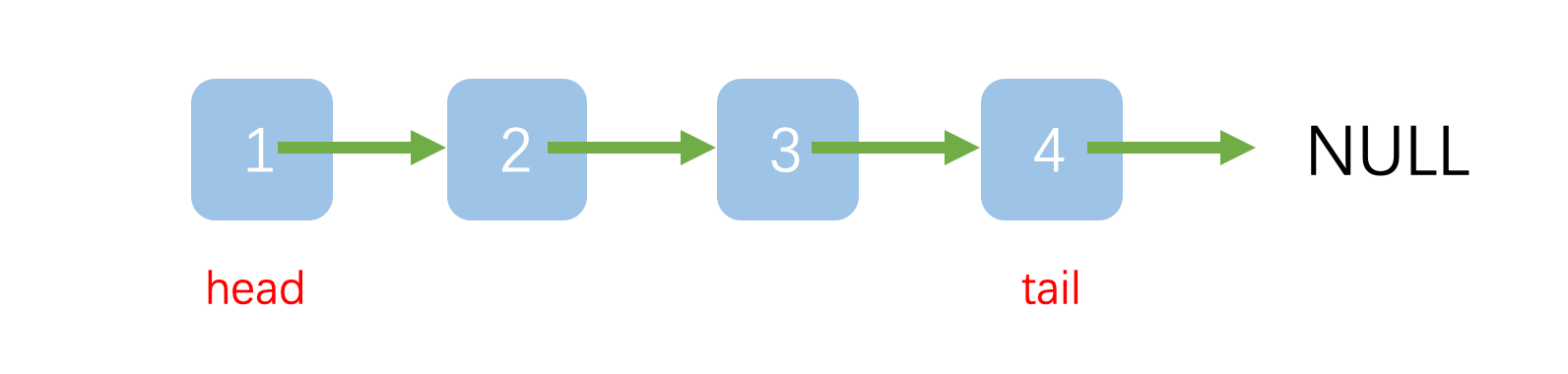
head ,因此可以很快的定位的表头,同样的我们可以设置一个tail变量,这样对于两端插入元素都是很容易。
这样队列从head端删除元素,从tail端插入元素。
head 队首负责出队,tail队尾负责入队。
Reference
- 在数据结构中穿针引线:链表(一)- https://cxyxiaowu.com/articles/2019/04/04/1554344901784.html
- 在数据结构中穿针引线:链表实现栈和队列 - https://cxyxiaowu.com/articles/2019/04/04/1554344924081.html