Background
队列（Queue）
队列的特点是什么？
聪明的小伙伴们都知道，是先进先出（FIFO）。
入队列：
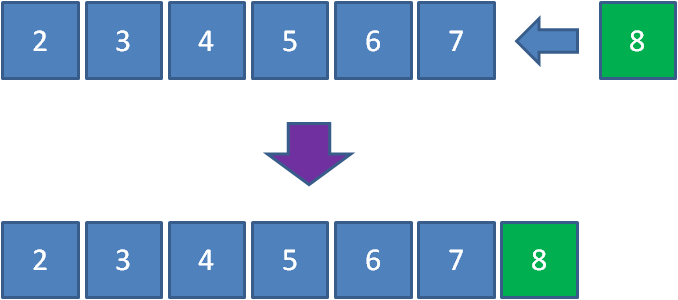
出队列：
优先队列（Priority Queue）
因为队列中允许的操作是先进先出（FIFO），在队尾插入元素，在队头取出元素。
而优先队列，不再遵循先入先出的原则，而是分为两种情况：
- 最大优先队列，无论入队顺序，当前最大的元素优先出队。
- 最小优先队列，无论入队顺序，当前最小的元素优先出队。
比如有一个最大优先队列，它的最大元素是8，那么虽然元素8并不是队首元素，但出队的时候仍然让元素8首先出队：
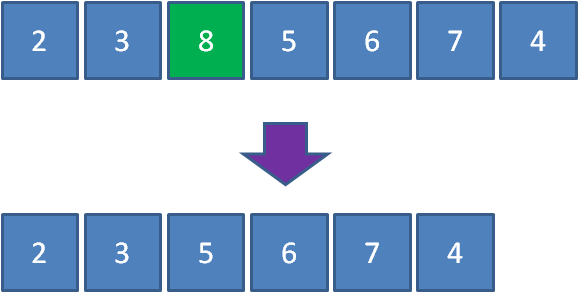
要满足以上需求，利用线性数据结构（比如，无序数组、有序数组或者链表）并非不能实现，只是时间复杂度较高（最坏时间复杂度O(n)），因而不是最理想的方式。
In computer science, a priority queue is an abstract data-type similar to a regular queue or stack data structure. Each element in a priority queue has an associated priority. In a priority queue, elements with high priority are served before elements with low priority. In some implementations, if two elements have the same priority, they are served in the same order in which they were enqueued. In other implementations, the order of elements with the same priority is undefined.
While priority queues are often implemented using heaps, they are conceptually distinct from heaps. A priority queue is an abstract data structure like a list or a map; just as a list can be implemented with a linked list or with an array, a priority queue can be implemented with a heap or another method such as an unordered array.
优先队列的操作
insert(key, data)：插入键值为key的数据到优先队列中，元素以其key进行排序；deleteMin/deleteMax：删除并返回最小/最大键值的元素；getMinimum/getMaximum：返回最小/最大剑指的元素，但不删除它；
优先队列的应用
- 数据压缩：赫夫曼编码算法；
- 最短路径算法：Dijkstra算法；
- 最小生成树算法：Prim算法；
- 事件驱动仿真：顾客排队算法；
- 选择问题：查找第k个最小元素；
- 等等等等….
顾客排队算法
优先队列的实现方式
优先队列有以下实现方式：
-
无序数组
-
有序数组
-
链表
-
堆（Heap）
- 二叉堆（Binary Heap）
- 二项式堆（pairing heaps）
- 斐波纳契堆（Fibonacci heaps）
-
二叉查找树
注意，堆是实现优先队列（Priority Queue）较为高效的方式，因此，在不严谨的情况下，我们有时也将堆和优先队列相互等同。
基于无序数组的优先队列实现
无序数组实现方式的入队操作，直接把入队元素加到数组尾部。出队需要遍历数组，找出优先级别最高的出队，空缺的位置由后面元素依次补上。因此，入队的时间复杂度为O(1)，出队为O(N)。
基于有序数组的优先队列实现
由于要求数组有序，因此在插入的时候需要保存有序，插入操作需要找到适合的位置，然后在该位置插入，位置后面的元素依次往后移动，时间复杂度为O(n)。而出队，由于序列是有序，可以在O(1)内出队。
基于链表的优先队列实现
链表的实现和有序数组的实现原理上相似，不同的是队列元素采用链式存储结构。可以使用有序链表和无序链表。
基于二叉堆（Binary Heap）的优先队列实现
基于完全二叉树（complete binary tree），是实现堆的一个经典方式，称为二叉堆（binary heap），而又由于其它几种堆用的较少，包括二项式堆（pairing heaps），斐波纳契堆（Fibonacci heaps）等，因此一般说堆，就是指二叉堆（binary heap）。
Refer to https://swsmile.info/post/data-structure-heap/
Reference
-
优先队列原理与实现 - https://www.cnblogs.com/luoxn28/p/5616101.html