队列(Queue)
通常,称进数据的一端为 “队尾”(rear),出数据的一端为 “队头”(top),数据元素进队列的过程称为 “入队(enqueue)",出队列的过程称为 “出队(dequeue)"。
不仅如此,队列中数据的进出要遵循 “先进先出” 的原则,即最先进队列的数据元素,同样要最先出队列。
栈和队列不要混淆,栈结构是一端封口,特点是"先进后出”;而队列的两端全是开口,特点是"先进先出”。
因此,数据从表的一端进,从另一端出,且遵循 “先进先出(First-In-First-Out,FIFO)” 原则的线性存储结构就是队列。
性能
| 接口 | 说明 | 复杂度 |
|---|---|---|
| void enqueue(E e) | 入队 | O(1) * |
| E dequeue() | 出队 | O(n) |
| E getFront() | 获取队首元素 | O(1) |
| int getSize() | 获取队列元素个数 | O(1) |
| boolean isEmpty() | 判断队列是否为空 | O(1) |
注意,入队操作从队尾进行,有可能触发resize(此时时间复杂度为 O(N)),而平均时间复杂度为 O(1)。
队列的实现
队列存储结构的实现有以下两种方式:
- 顺序队列:在数组的基础上实现的队列结构;
- 链队列:在链表的基础上实现的队列结构;
两者的区别仅是顺序表和链表的区别,即在实际的物理空间中,数据集中存储的队列是顺序队列,分散存储的队列是链队列。
顺序队列简单实现
由于顺序队列的底层使用的是数组,因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外,为了满足顺序队列中数据从队尾进,队头出且先进先出的要求,我们还需要定义两个指针(top 和 rear)分别用于指向顺序队列中的队头元素和队尾元素,如下图所示:
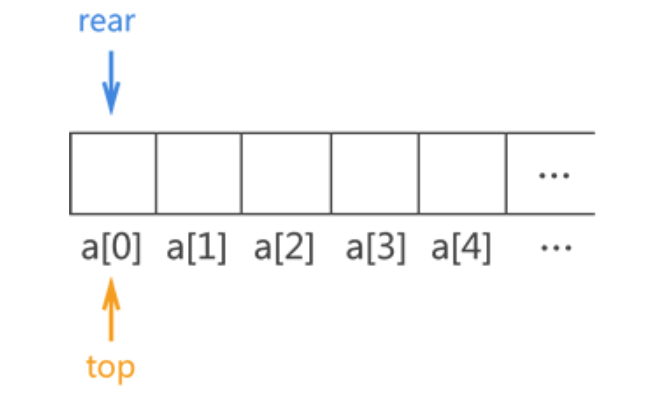
由于顺序队列初始状态没有存储任何元素,因此 top 指针和 rear 指针重合,且由于顺序队列底层实现靠的是数组,因此 top 和 rear 实际上是两个变量,它的值分别是队头元素和队尾元素所在数组位置的下标。
在上图的基础上,当有数据元素进队列时,对应的实现操作是将其存储在指针 rear 指向的数组位置,然后 rear+1;当需要队头元素出队时,仅需做 top+1 操作。
例如,在上图基础上将 {1,2,3,4} 用顺序队列存储的实现操作如下图所示:
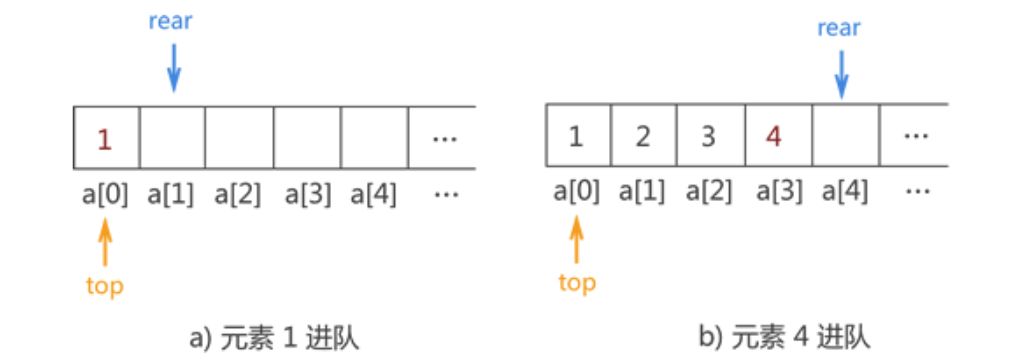
在上图基础上,顺序队列中数据出队列的实现过程如下图所示:
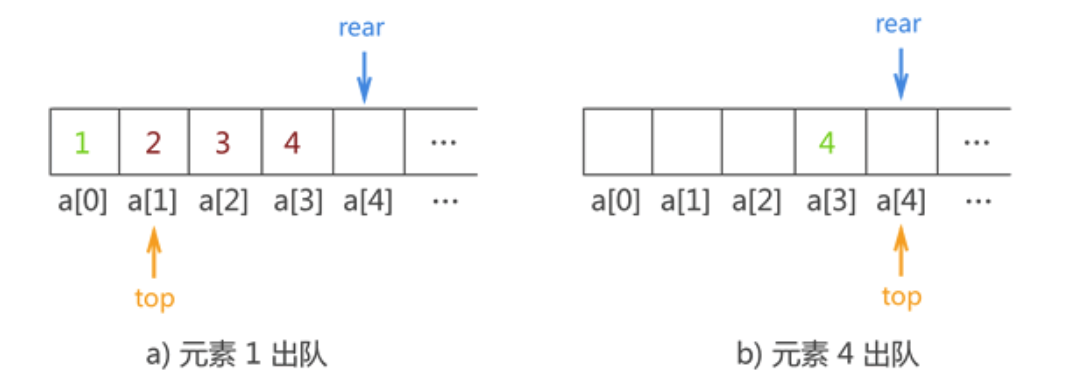
通过对比在所有元素入队之前和所有元素出队之后的状态,你会发现,指针 top 和 rear 重合位置指向了 a[4] 而不再是 a[0]。也就是说,整个顺序队列在数据不断地进队出队过程中,在顺序表中的位置不断后移。
顺序队列整体后移造成的影响是:
- 顺序队列之前的数组存储空间将无法再被使用,造成了空间浪费;
- 如果顺序表申请的空间不足够大,则直接造成程序中数组 a 溢出,产生溢出错误;
顺序队列另一种实现方法 - 循环队列
既然明白了上面这种方法的弊端,那么我们可以试着在它的基础上对其改良。
为了解决以上两个问题,可以使用巧妙的方法将顺序表打造成一个环状表,如下图所示:
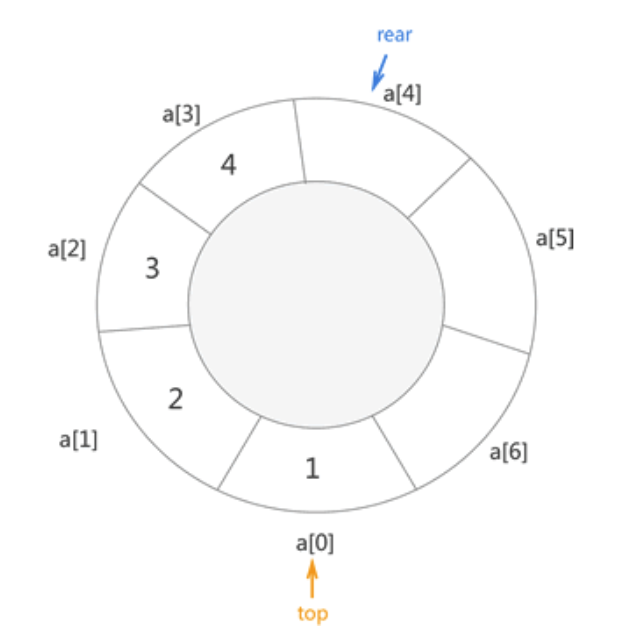
链表队列的实现
链式队列的实现思想同顺序队列类似,只需创建两个指针(命名为 top 和 rear)分别指向链表中队列的队头元素和队尾元素,如下图所示:
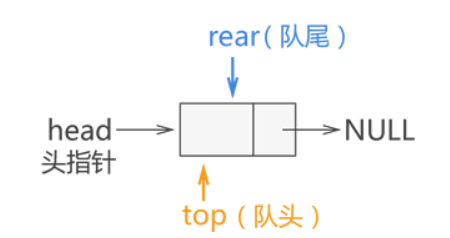
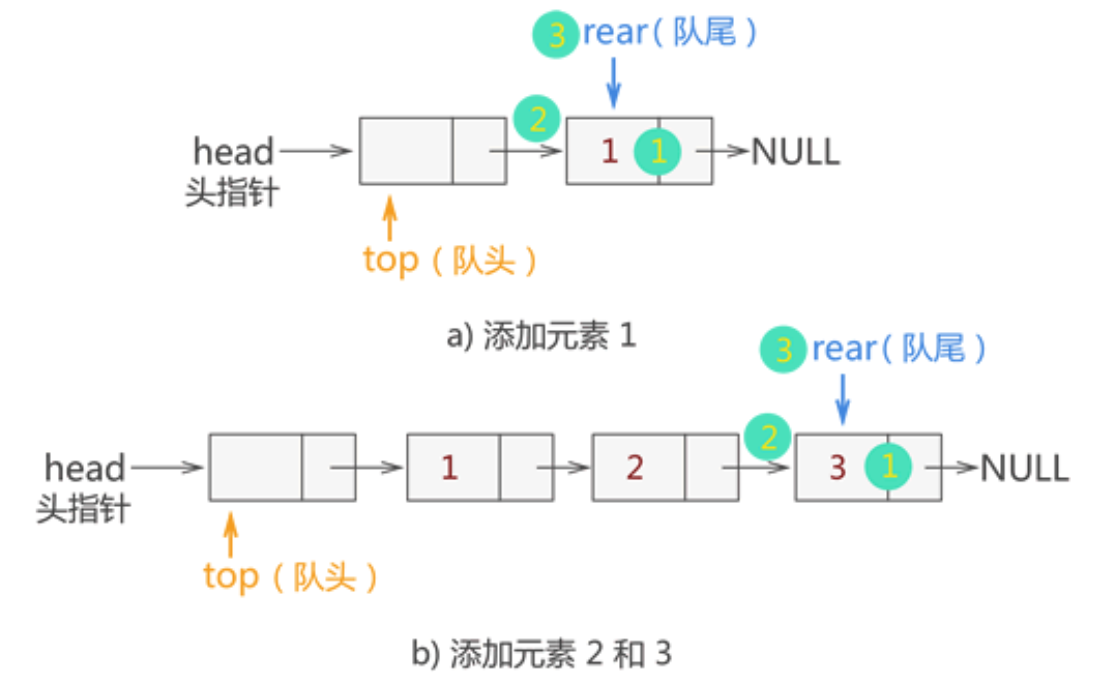
例如,在上图的基础上,我们依次将 {1,2,3} 依次入队,各个数据元素入队的过程如下图所示:
Reference
- 数据结构概述 - http://data.biancheng.net/intro/