红黑树(Red-Black Tree)
在 1972 年,慕尼黑理工大学(Technical University of Munich)的计算机科学家 Rudolf Bayer 创造了**红黑树(Red-Black Tree)**数据结构。
除了包含数据和左右孩子节点之外,红黑树的节点还包含了一项特别的信息 – 颜色。这个颜色只包含两种颜色,即红色和黑色。
并且,红黑树还添加了一种特殊类型的节点,称为 NIL 节点。NIL 节点将做为红黑树的伪叶子节点出现。也就是说,所有带有关键数据的节点称为内节点,而所有其他的外节点则均指向 NIL 节点。这个概念可能理解起来有些费劲,希望下面这张图有所帮助。
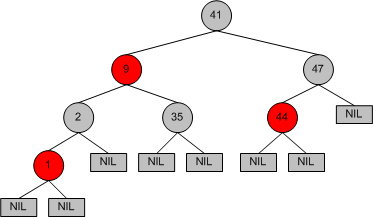
红黑树性质
红黑树(R-B Tree)需要满足如下性质:
- 节点的颜色只能是红色或者黑色;
- 根节点是黑色的(根性质);
- NIL 节点的颜色是黑色;
- 如果节点的颜色是红色,则其子节点均为黑色(红性质);
- 从任一节点到其后代任一叶子节点的路径上的黑色节点的数量相同(黑性质);
前面几条性质都很好解释,只有最后一条最难理解。简单的说,从树中任意一个节点开始,从该节点到其后代的任意一个 NIL 节点的路径上的黑色节点的数量必须相同。比如上图中,以根节点为例,从节点 41 到任意一个 NIL 节点的路径上,黑色节点的数量都是相同的,也就是 3 个。如从节点 41 到左下角的 NIL 节点的路径上,黑色节点包括 41, 2, NIL,所以黑色节点数量是 3 个。
性能
类似于 AVL 树,红黑树也是一种自平衡二叉查找树。AVL 树的平衡性质是通过限制节点的左右子树的高度来达成,而红黑树则是通过更形象化的方式来保证树的平衡。如果一棵树满足红黑树的性质,其节点的总数量为 n,则它的高度将始终小于 $2 * log_2(n+1)$ 。鉴于这个原因,致使红黑树保证了对树的所有操作的最坏时间复杂度为 $O(log_2n)$。
红黑树的平衡插入
同样是和 AVL 树一样,当对红黑树进行节点的插入和删除时,最终要的就是使其仍然符合红黑树的性质。AVL 树通过使用**旋转操作(rotations)来恢复树的平衡。而红黑树则是通过重新着色(recoloring)**和旋转两种操作共同来完成。这不仅需要判断节点的父节点的颜色,还需要对比叔父节点的颜色,使得红黑树的恢复过程变得更加复杂。
变色(recoloring)
为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色。
下图所表示的是红黑树的一部分,需要注意节点25并非根节点。因为节点21和节点22连续出现了红色,不符合规则4(如果节点的颜色是红色,则其子节点均为黑色),所以把节点22从红色变成黑色(变色后如下图所示):
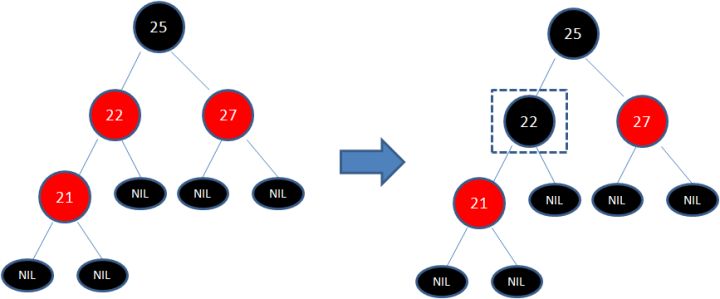
但这样并不算完,因为凭空多出的黑色节点打破了规则5(从任一节点到其后代任一叶子节点的路径上的黑色节点的数量相同),所以发生连锁反应,需要继续把节点25从黑色变成红色(变色后如下图所示):
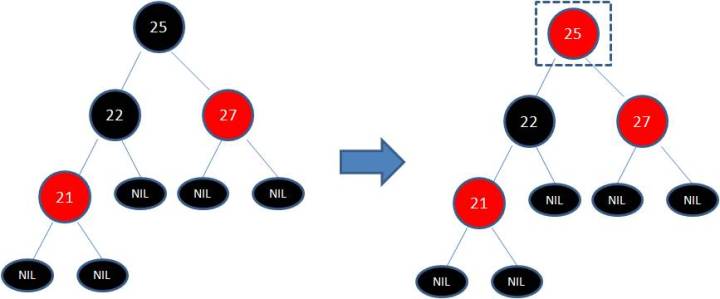
此时仍然没有结束,因为节点25和节点27又形成了两个连续的红色节点,因而违反了规则4(如果节点的颜色是红色,则其子节点均为黑色),需要继续把节点27从红色变成黑色:
旋转(rotations)
左旋转
逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。说起来很怪异,大家看下图:
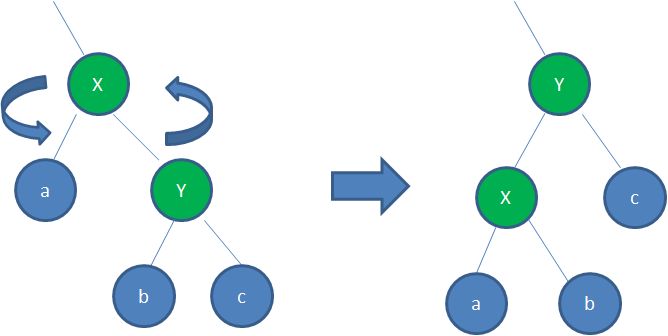
图中,身为右孩子的Y取代了X的位置,而X变成了自己的左孩子。此为左旋转。
右旋转
顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。大家看下图:
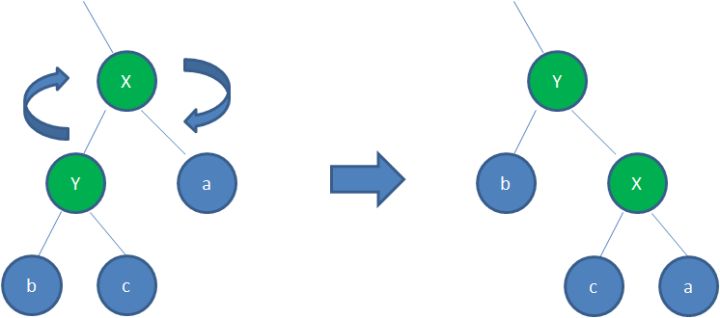
图中,身为左孩子的Y取代了X的位置,而X变成了自己的右孩子。此为右旋转。
调整思想
红黑树的第 5 条特征规定,任一节点到它子树的每个叶子节点的路径中都包含同样数量的黑节点。也就是说当我们往红黑树中插入一个黑色节点时,会违背这条特征。
同时第 4 条特征规定红色节点的左右孩子一定都是黑色节点,当我们给一个红色节点下插入一个红色节点时,会违背这条特征。
因此我们需要在插入黑色节点后进行结构调整,保证红黑树始终满足这 5 条特征。
前面说了,插入一个节点后要担心违反特征 4 和 5,数学里最常用的一个解题技巧就是把多个未知数化解成一个未知数。我们这里采用同样的技巧,把插入的节点直接染成红色,这样就不会影响特征 5,只要专心调整满足特征 4 就好了。这样比同时满足 4、5 要简单一些。
染成红色后,我们只要关心父节点是否为红,如果是红的,就要把父节点进行变化,让父节点变成黑色,或者换一个黑色节点当父亲,这些操作的同时不能影响 不同路径上的黑色节点数一致的规则。
【插入、染红后的调整有 2 种情况:】
情况1.父亲节点和叔叔节点都是红色:
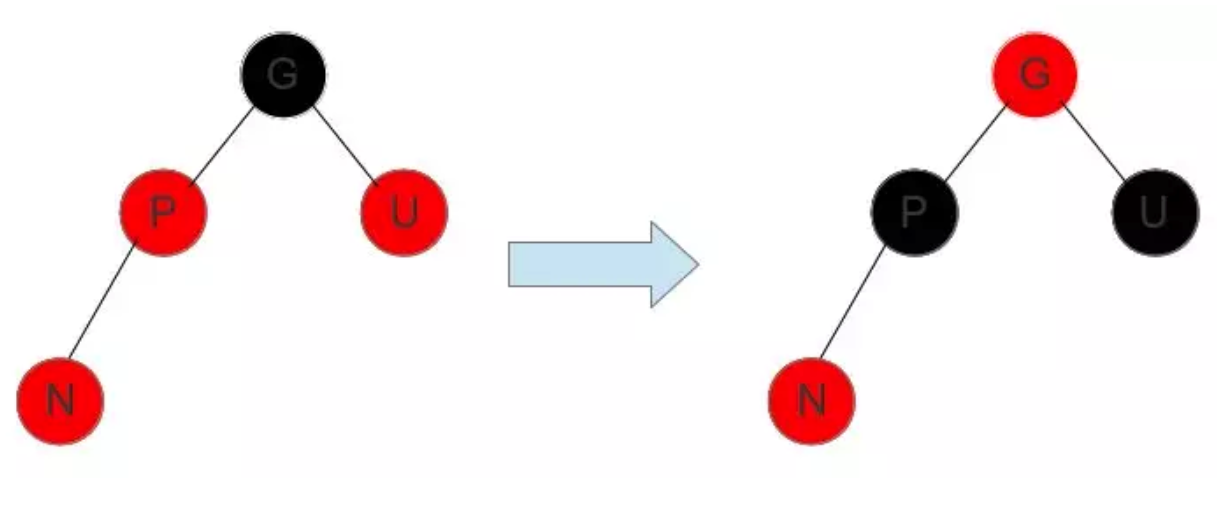
假设插入的是节点 N,这时父亲节点 P 和叔叔节点 U 都是红色,爷爷节点 G 一定是黑色。
红色节点的孩子不能是红色,这时不管 N 是 P 的左孩子还是右孩子,只要同时把 P 和 U 染成黑色,G 染成红色即可。这样这个子树左右两边黑色个数一致,也满足特征 4。
但是这样改变后 G 染成红色,G 的父亲如果是红色岂不是又违反特征 4 了? 这个问题和我们插入、染红后一致,因此需要以 爷爷节点 G 为新的调整节点,再次进行调整操作,以此循环,直到父亲节点不是红的,就没有问题了。
情况2.父亲节点为红色,叔叔节点为黑色:
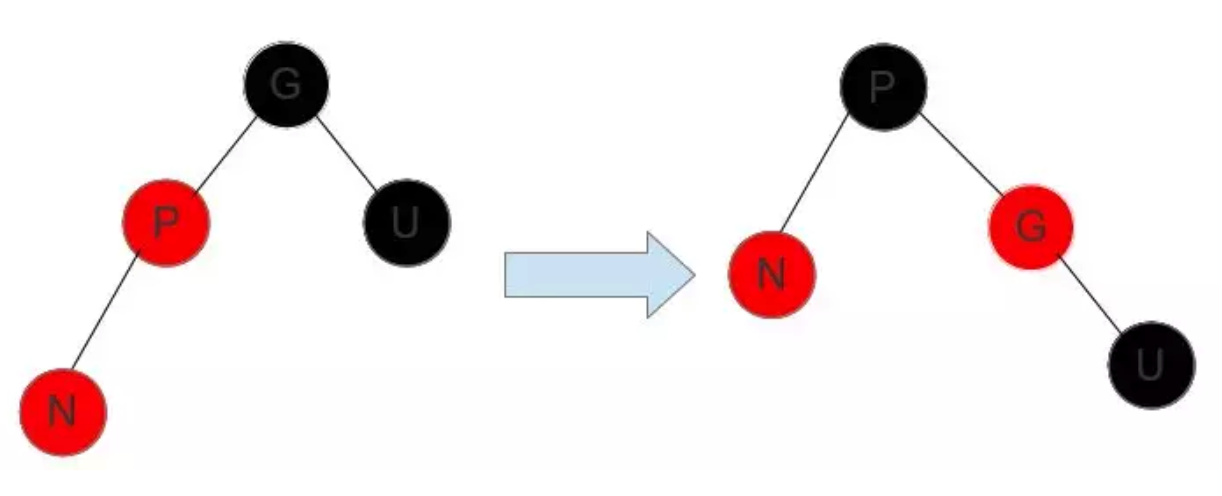
假设插入的是节点 N,这时父亲节点 P 是红色,叔叔节点 U 是黑色,爷爷节点 G 一定是黑色。
红色节点的孩子不能是红色,但是直接把父亲节点 P 涂成黑色也不行,这条路径多了个黑色节点。怎么办呢?
既然改变不了你,那我们就此别过吧,我换一个更适合我的!
我们怎么把 P 弄走呢?看来看去,还是右旋最合适,通过把 爷爷节点 G 右旋,P 变成了这个子树的根节点,G 变成了 P 的右子树。
右旋后 G 跑到了右子树上,这时把 P 变成黑的,多了一个黑节点,再把 G 变成红的,就平衡了!
上面讲的是插入节点 N 在父亲节点 P 的左孩子位置,如果 N 是 P 的右孩子,就需要多进行一次左旋,把情况化解成上述情况。
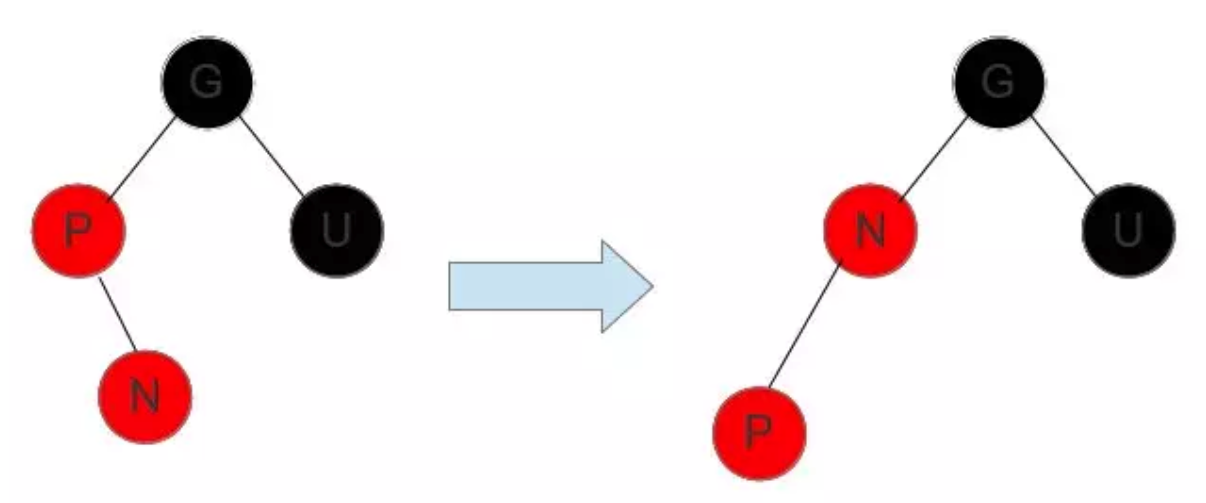
N 位于 P 的右孩子位置,将 P 左旋,就化解成上述情况了。
红黑树的平衡删除
红黑树的插入平衡需要好好理解下,如果前面没有理解,删除后的调整平衡更加难懂,前方高能,请注意!
红黑树的删除也是分两步:
- 二叉查找树的删除
- 结构调整
二叉查找树的删除
1.要删除的节点正好是叶子节点,直接删除就 OK 了(右图有错误,应该是 z 不是 r)
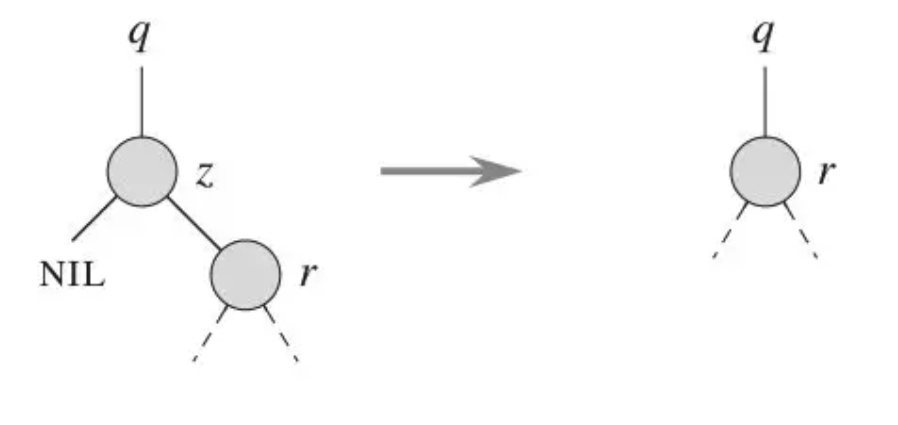
2.有左孩子或者右孩子,直接把这个孩子上移放到要删除的位置就好了
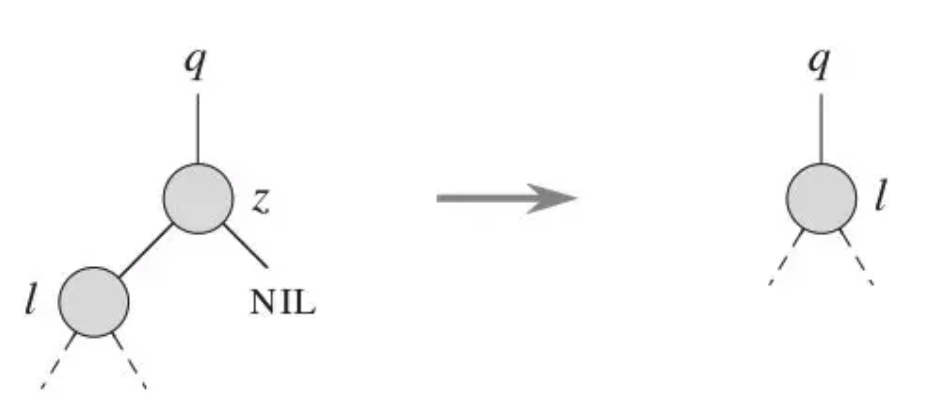
3.有两个孩子,就需要选一个合适的孩子节点作为新的根节点,该节点称为 继承节点
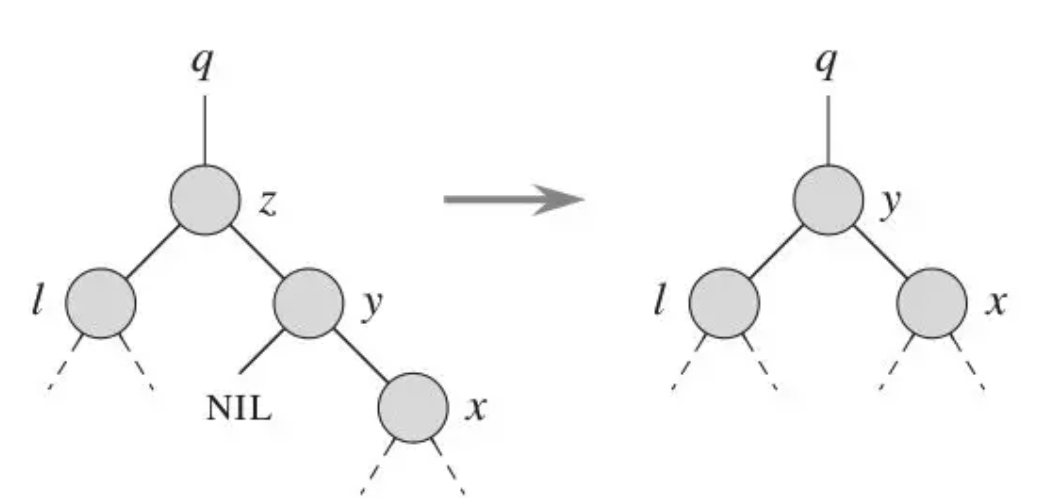
删除后的结构调整
根据红黑树的第 5 个特性:
如果当前待删除节点是红色的,它被删除之后对当前树的特性不会造成任何破坏影响。 而如果被删除的节点是黑色的,这就需要进行进一步的调整来保证后续的树结构满足要求。
这里研究的是删除黑色节点的情况。
调整思想
为了保证删除节点父亲节点左右两边黑色节点数一致,需要重点关注父亲节点没删除的那一边节点是不是黑色。如果删除后父亲节点另一边比删除的一边黑色节点多,就要想办法搞到平衡,具体的平衡方法有如下几种方法:
- 把父亲节点另一边(即删除节点的兄弟树)其中一个节点弄成红色,也少一个黑色
- 或者把另一边多的黑色节点转过来一个
删除节点在父亲节点的左子树还是右子树,调整方式都是对称的,这里以当前节点为父节点的左孩子为例进行分析。
【删除后的调整主要分三步】:
第一步:
- 兄弟如果是红的,说明孩子都是黑的【旋转的情况 1 】
- 把兄弟搞成黑的
- 父亲搞成红的
- 左旋转父亲(嘿嘿,兄弟给我分一个黑孩子)
- 接下来对比旋转后的兄弟
第一步解释:
这一步的目的是将兄弟节点变成黑的,转变成第二步两种情形中的某一种情况。
在做后续变化前,这棵树还是保持着原来的平衡。
第二步,有两种情况:
情况1 :兄弟节点的孩子都是黑色
- 把兄弟搞成红的
- continue 下一波(这个子树搞完了,研究父亲节点,去搞上一级树,进入第三步)
第二步情况 1 解释:
这里将兄弟节点变成红色后,从它的父节点到下面的所有路径就都统一少了 1 个,同时也不影响别的特征,但是把兄弟节点变红后,如果有父亲节点也是红的,就可能违反红黑树的特征 4,因此需要到更高一级树进行鉴别、调整。
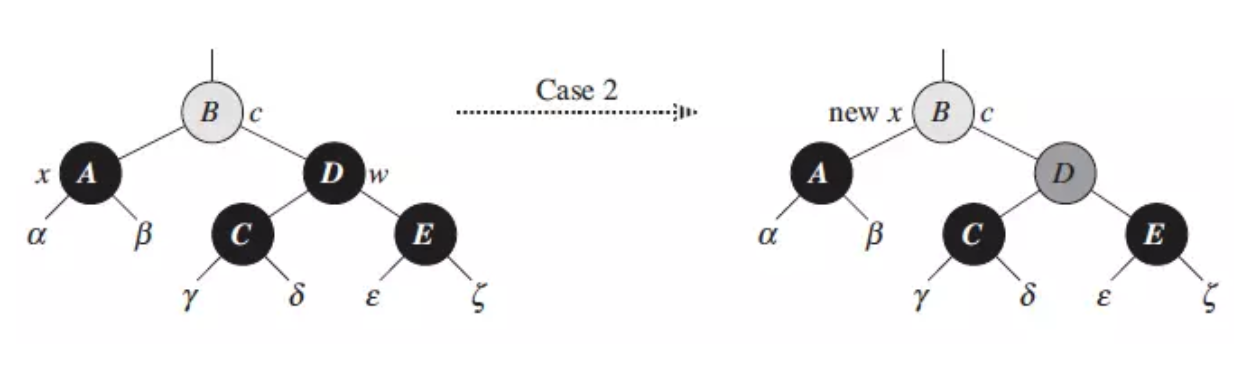
情况2 :兄弟节点的孩子至多有一个是黑的
- 把不是黑的那个孩子搞黑【旋转的情况 2 】
- 兄弟搞红
- 兄弟右旋转
- 以后对比旋转后的兄弟
- 把兄弟涂成跟父亲一样的颜色 【旋转的情况 3 】
- 然后把父亲搞黑
- 把兄弟的右孩子搞黑
- 父亲节点左旋
- 研究根节点,进入第三步
第二步情况 2 解释:
旋转的情况 2 是将兄弟节点的左右孩子都移动到右边,方便后续操作,如下图所示:
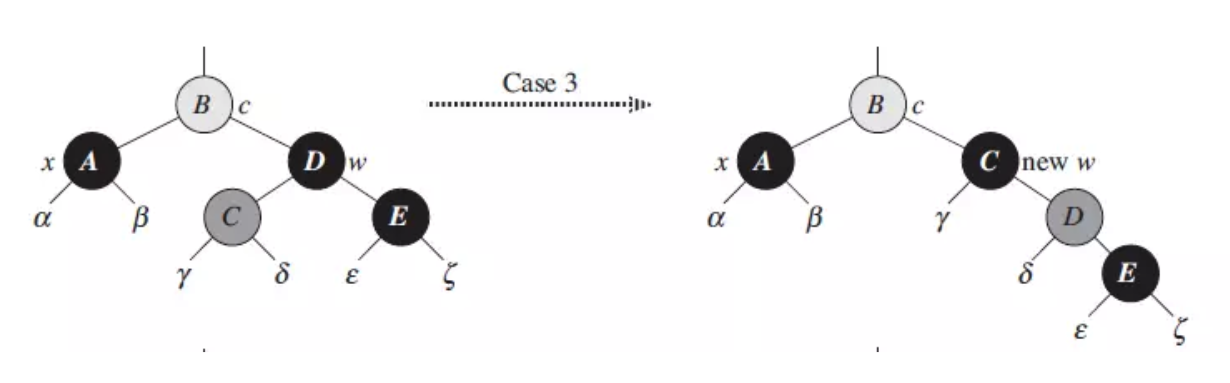
旋转的情况 3 将兄弟的孩子移到左边来,同时黑色的父亲变到了左边(总之就是让左边多些黑色节点),如下图所示:
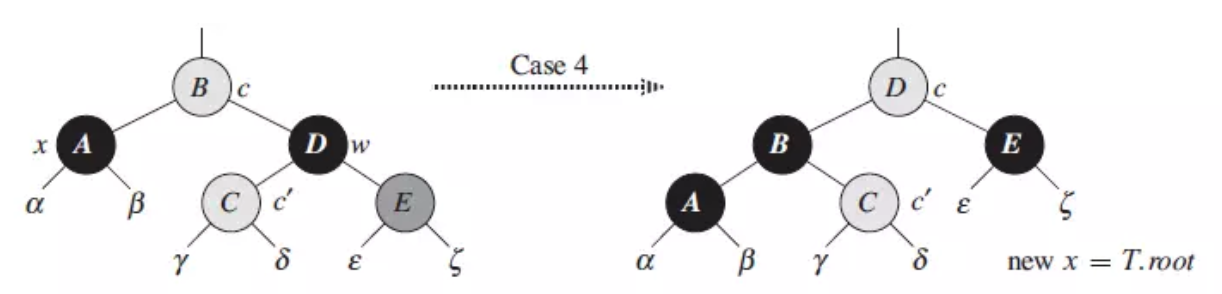
第三步:
- 如果研究的不是根节点并且是黑的,重新进入第一步,研究上一级树;
- 如果研究的是根节点或者这个节点不是黑的,就退出
- 把研究的这个节点涂成黑的。
第三步解释:
第三步中选择根节点为结束标志,是因为在第二步中,有可能出现我们正好给删除黑色节点的子树补上了一个黑色节点,同时不影响其他子树,这时我们的调整已经完成,可以直接设置调整节点 x = root,等于宣告调整结束。
因为我们当前调整的可能只是一棵树中间的子树,这里头的节点可能还有父节点,这么一直往上到根节点。当前子树少了一个黑色节点,要保证整体合格还是不够的。
这里需要在代码里有一个保证。假设这里 B 已经是红色的了。那么调整结束,最后对 B 节点,也就是调整目标 x 所指向的这个节点涂成黑色。这样保证前面亏的那一个黑色节点就补回来了。
前面讨论的这4种情况是在当前节点是父节点的左子节点的条件下进行的。如果当前节点是父节点的右子节点,则可以对应的做对称的操作处理,过程也是一样的。
其中具体旋转方向根据调整节点在父节点的左/右位置决定。
Reference
- 自平衡二叉查找树 - https://www.cnblogs.com/gaochundong/p/self_balancing_binary_search_tree.html
- 一篇搞懂AVL平衡二叉树 - https://zhuanlan.zhihu.com/p/34840762、
- 【算法】论平衡二叉树(AVL)的正确种植方法 - https://www.cnblogs.com/penghuwan/p/8166133.html
- 漫画:什么是红黑树? - https://zhuanlan.zhihu.com/p/31805309
- 面试旧敌之红黑树(直白介绍深入理解) - https://juejin.im/entry/58371f13a22b9d006882902d
- https://www.cnblogs.com/nullzx/p/6128416.html