背景
- Binary tree:二叉树(Binary tree),每个节点只能存储一个key
- B-tree:B树(B-Tree,并不是B“减”树,横杠为连接符,容易被误导)
- B树属于多叉树,同时也属于平衡多路查找树。每个节点可以包含多个key(包含多少个由磁盘的页的大小决定)。
- B+tree(B+树) 和 B*tree(B*树) 都是 B-tree 的变种
B 树(B-tree)
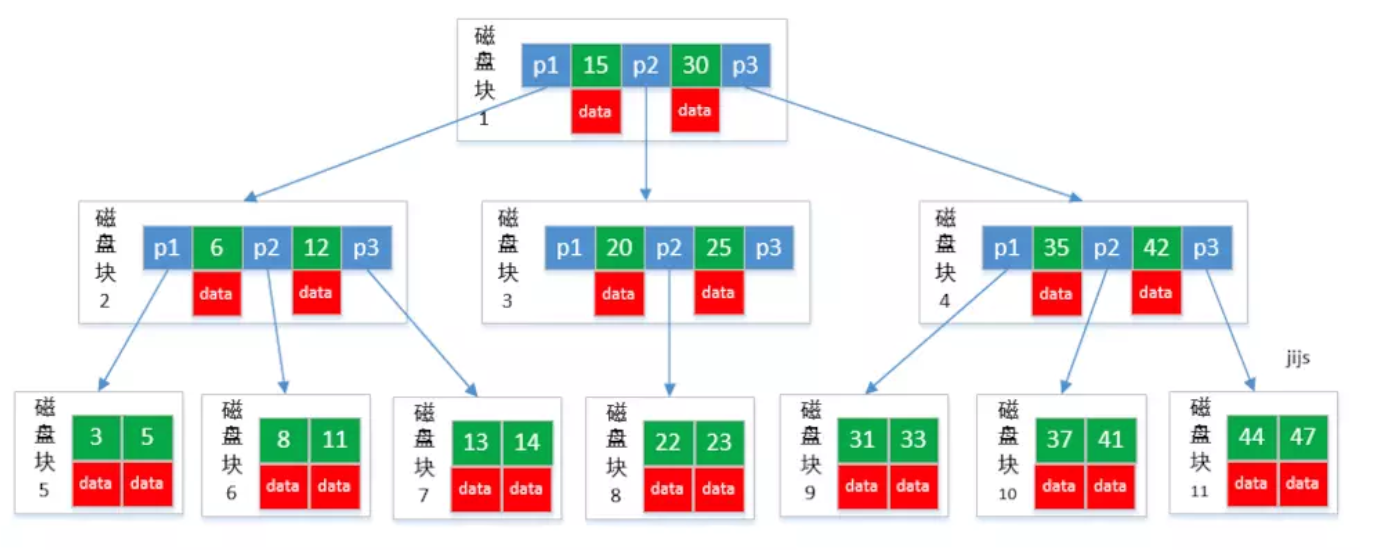
从图中可以看出,B-tree 利用了磁盘块/页的特性进行构建的树。每个磁盘块/页的大小正好等于B树的一个节点的大小,每个节点包含了键(key)和值(value)。
我们知道,操作系统每次从磁盘读取数据到内存都是以页作为最小单位的,而一页通常等于n个扇区。上图中所示的磁盘块/页与操作系统每次从磁盘读取数据到内存的页的大小正好相等。如果要访问B树中的一个节点,进行I/O操作的次数等于该节点在B树中的深度。
而通过把树中节点可以包含的键(key)的个数增加,树的高度就比其对应的二叉树矮了,最终就减少了进行单次数据查找时,进行I/O操作的次数。
B-tree巧妙利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入,B-tree 的数据可以存在任何节点中。
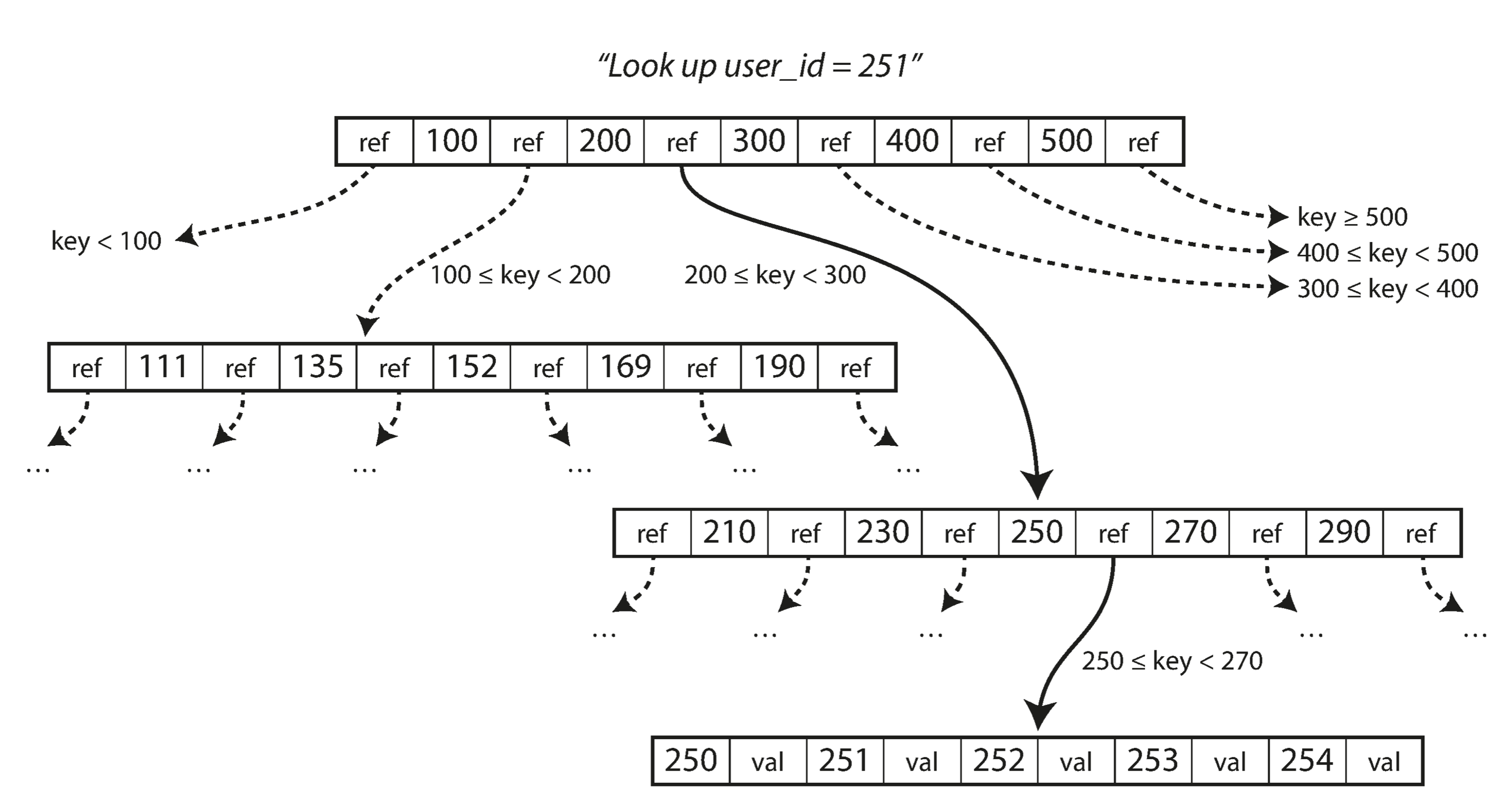
One page is designated as the root of the B-tree; whenever you want to look up a key in the index, you start here. The page contains several keys and references to child pages. Each child is responsible for a continuous range of keys, and the keys between the references indicate where the boundaries between those ranges lie.
In the example in below, we are looking for the key 251, so we know that we need to follow the page reference between the boundaries 200 and 300. That takes us to a similar-looking page that further breaks down the 200–300 range into subranges.
Eventually we get down to a page containing individual keys (a leaf page), which either contains the value for each key inline or contains references to the pages where the values can be found.
The number of references to child pages in one page of the B-tree is called the branching factor. For example, in the example below the branching factor is six. In practice, the branching factor depends on the amount of space required to store the page references and the range boundaries, but typically it is several hundred.
If you want to update the value for an existing key in a B-tree, you search for the leaf page containing that key, change the value in that page, and write the page back to disk (any references to that page remain valid). If you want to add a new key, you need to find the page whose range encompasses the new key and add it to that page. If there isn’t enough free space in the page to accommodate the new key, it is split into two half-full pages, and the parent page is updated to account for the new subdivision of key ranges—see below.
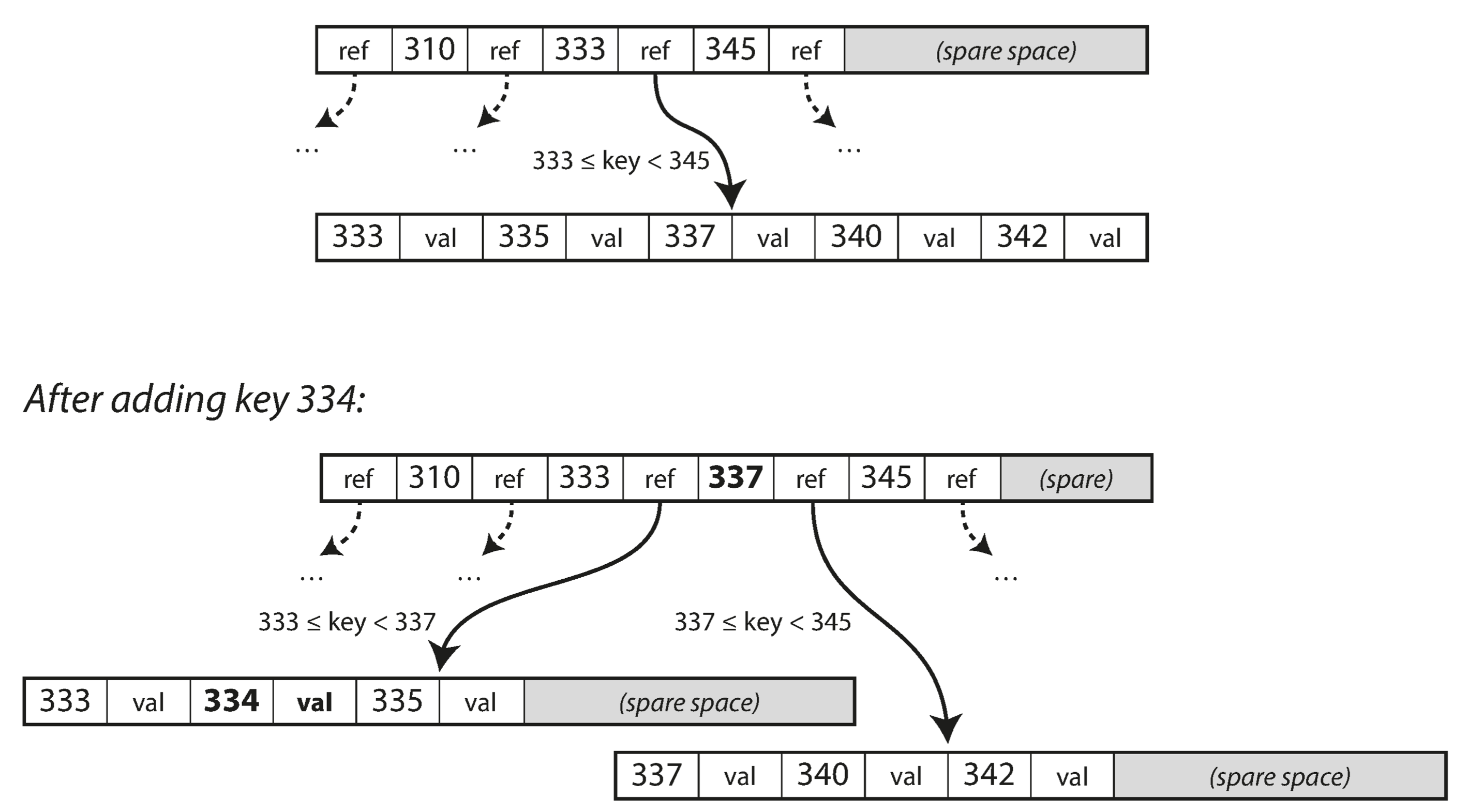
This algorithm ensures that the tree remains balanced: a B-tree with n keys always has a depth of O(log n). Most databases can fit into a B-tree that is three or four levels deep, so you don’t need to follow many page references to find the page you are looking for. (A four-level tree of 4 KB pages with a branching factor of 500 can store up to 256 TB.)
B+ 树(B+ tree)
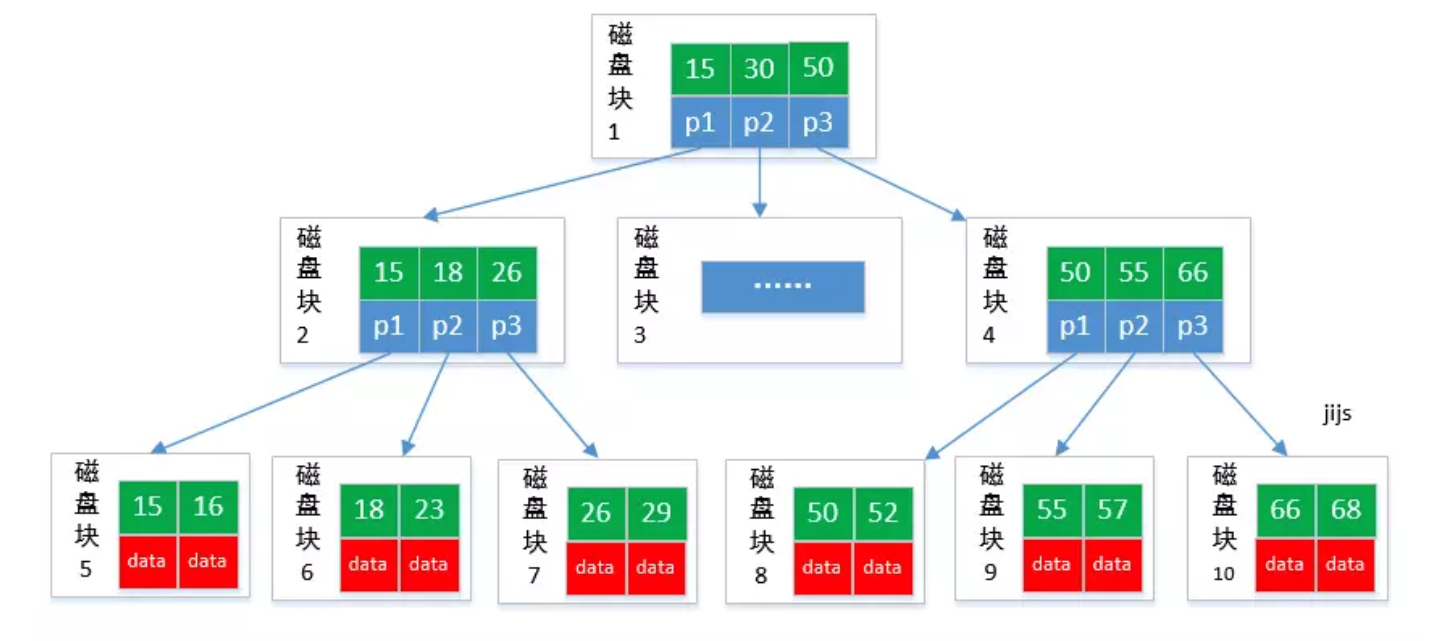
B+ 树(B+ tree)是 B-tree 的变种,两者的区别在于,B+ 树的数据(或者说键值的值)只能存储在叶子节点中。
这样,在B树的基础上每个节点存储的关键字数就更多,自然地,树的深度更少,因此查询数据更快。
为什么使用B树或B+树作为索引
理论上,红黑树等数据结构也可以用来实现索引,但是文件系统及数据库系统普遍采用B树或B+树作为索引结构。
一般来说,索引本身也很大,不可能全部存储在内存中,因此索引往往以索引文件的形式存储在磁盘上。这样的话,索引查找过程中就要进行磁盘I/O操作。相对于对内存存取,进行磁盘的I/O操作的时间消耗要高几个数量级,所以评价一个数据结构作为索引的优劣最重要的指标,就是在查找过程中磁盘I/O操作次数的渐进复杂度。换句话说,索引的结构组织要尽量实现在找过程中进行最少次数的磁盘I/O操作操作。
而B树和B+树,可以有效的利用系统对磁盘的块读取特性,同时尽可能多的加载索引数据,来提高索引命中效率,最终达到减少磁盘I/O的读取次数。
与红黑树的比较
红黑树等平衡树也可以用来实现索引,但是文件系统及数据库系统普遍采用 B+ Tree 作为索引结构,主要有以下两个原因:
1 更少的I/O操作次数
平衡树查找操作的时间复杂度和树高 h 相关,$O(h)=O(log_dN)$,其中 d 为每个节点的出度。
红黑树的出度为 2,而 B+ Tree 的出度一般都非常大,所以红黑树的树高 h 很明显比 B+ Tree 大非常多,I/O操作次数也就更多。
主存存取原理
目前计算机使用的主存基本都是随机读写存储器(RAM),现代RAM的结构和存取原理比较复杂,这里本文抛却具体差别,抽象出一个十分简单的存取模型来说明RAM的工作原理。
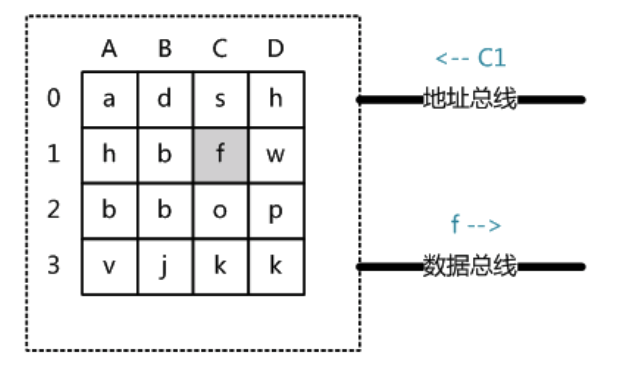
从抽象角度看,主存是一系列的存储单元组成的矩阵,每个存储单元存储固定大小的数据。每个存储单元有唯一的地址,现代主存的编址规则比较复杂,这里将其简化成一个二维地址:通过一个行地址和一个列地址可以唯一定位到一个存储单元。上图展示了一个4 x 4的主存模型。
主存的存取过程如下:
当系统需要读取主存时,则将地址信号放到地址总线上传给主存,主存读到地址信号后,解析信号并定位到指定存储单元,然后将此存储单元数据放到数据总线上,供其它部件读取。
写主存的过程类似,系统将要写入单元地址和数据分别放在地址总线和数据总线上,主存读取两个总线的内容,做相应的写操作。
这里可以看出,主存存取的时间仅与存取次数呈线性关系。因为不存在机械操作,两次存取的数据的“距离”不会对时间有任何影响,例如,取A0、A1的时间总消耗,和取A0、D3的时间总消耗是一样的。
磁盘存取原理
上文说过,索引一般以文件形式存储在磁盘上,索引检索需要磁盘I/O操作。与主存不同,磁盘I/O存在机械运动耗费,因此磁盘I/O的时间消耗是巨大的。
下图是磁盘的整体结构示意图:
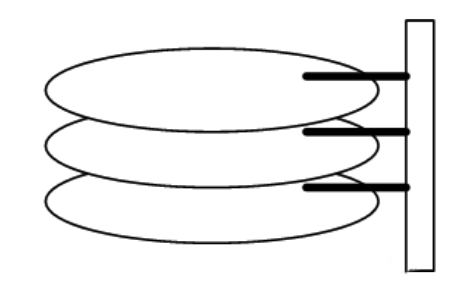
一个磁盘由大小相同且同轴的圆形盘片组成,磁盘可以转动(各个磁盘必须同步转动)。在磁盘的一侧有磁头支架,磁头支架固定了一组磁头(disk head),每个磁头负责存取一个磁盘的内容。磁头不能转动,但是可以沿磁盘半径方向运动(实际是斜切向运动),每个磁头同一时刻也必须是同轴的,即从正上方向下看,所有磁头任何时候都是重叠的(不过目前已经有多磁头独立技术,可不受此限制)。
下图是磁盘结构的示意图:
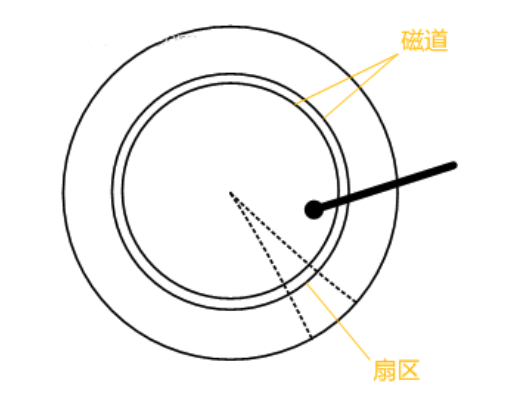
盘片被划分成一系列同心环,圆心是盘片中心,每个同心环叫做一个磁道,所有半径相同的磁道组成一个柱面。磁道被沿半径线划分成一个个小的段,每个段叫做一个扇区(Sector),每个扇区是磁盘的最小存储单元。为了简单起见,我们下面假设磁盘只有一个盘片和一个磁头。
当需要从磁盘读取数据时,系统会将数据逻辑地址传给磁盘,磁盘的控制电路按照寻址逻辑将逻辑地址翻译成物理地址,即确定要读的数据在哪个磁道,哪个扇区。为了读取这个扇区的数据,需要将磁头放到这个扇区上方,为了实现这一点,磁头需要移动对准相应磁道,这个过程叫做寻道(Seek),所耗费时间叫做寻道时间(seek time),然后磁盘旋转将目标扇区旋转到磁头下,这个过程耗费的时间叫做旋转时间。
局部性原理与磁盘预读
由于存储介质的特性,磁盘本身存取就比主存慢很多,再加上机械运动耗费,磁盘的存取速度往往是主存的几百分分之一,因此为了提高效率,要尽量减少磁盘I/O。为了达到这个目的,磁盘往往不是严格按需读取,而是每次都会预读,即使只需要一个字节,磁盘也会从这个位置开始,顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理:
当一个数据被用到时,其附近的数据也通常会马上被使用。
程序运行期间所需要的数据通常比较集中。
由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高I/O效率。
预读的长度一般为**页(page)**的整倍数。页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,每个存储块称为一页(在许多操作系统中,页的大小通常为4KB),主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
B树或B+树索引的性能分析
到这里终于可以分析B树或B+树作为索引的性能了。
上文说过一般使用磁盘I/O次数评价索引结构的优劣。先从B树分析,根据B树的定义,可知查找一个值最多需要访问h个节点。数据库系统的设计者巧妙利用了磁盘预读原理,将一个节点的占用大小等于一个页的大小,这样读取一个节点只需要进行一次I/O操作即可。为了达到这个目的,在实际实现B树时,还需要使用如下技巧:
- 每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上就存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了读取一个节点只需要进行一次I/O。
- B树中一次检索最多需要进行h-1次I/O(根节点常驻内存,h为树的高度),渐进复杂度为$O(h)=O(log_dN)$。一般实际应用中,树的度d是一个非常大的数字,通常超过100,因此h非常小(通常不超过3)。
综上所述,用B树作为索引结构效率是非常高的。
而红黑树这种结构,h明显要深的多。由于逻辑上很近的节点(父子)物理上可能很远,无法利用局部性,所以红黑树的I/O渐进复杂度也为O(h),但效率明显比B-Tree差很多(因为红黑树的深度比B-Tree要大很多)。
上文还说过,B+树更适合外存索引,原因和内节点的度d有关。从上面分析可以看到,d越大索引的性能越好,而内节点度的上限取决于内节点内key和data的大小:
$$ d_{max}=floor(pagesize/(keysize+datasize+pointsize)) $$ floor表示向下取整。由于B+树的内节点均去掉了data域,因此可以拥有更大的度,拥有更好的性能。
Making B-trees reliable
The basic underlying write operation of a B-tree is to overwrite a page on disk with new data. It is assumed that the overwrite does not change the location of the page; i.e., all references to that page remain intact when the page is overwritten. This is in stark contrast to log-structured indexes such as LSM-trees, which only append to files (and eventually delete obsolete files) but never modify files in place.
You can think of overwriting a page on disk as an actual hardware operation. On a magnetic hard drive, this means moving the disk head to the right place, waiting for the right position on the spinning platter to come around, and then overwriting the appropriate sector with new data. On SSDs, what happens is somewhat more compli‐cated, due to the fact that an SSD must erase and rewrite fairly large blocks of a storage chip at a time.
Moreover, some operations require several different pages to be overwritten. For example, if you split a page because an insertion caused it to be overfull, you need to write the two pages that were split, and also overwrite their parent page to update the references to the two child pages. This is a dangerous operation, because if the database crashes after only some of the pages have been written, you end up with a corrupted index (e.g., there may be an orphan page that is not a child of any parent).
In order to make the database resilient to crashes, it is common for B-tree implementations to include an additional data structure on disk: a write-ahead log (WAL, also known as a redo log). This is an append-only file to which every B-tree modification must be written before it can be applied to the pages of the tree itself. When the database comes back up after a crash, this log is used to restore the B-tree back to a consistent state.
An additional complication of updating pages in place is that careful concurrency control is required if multiple threads are going to access the B-tree at the same time —otherwise a thread may see the tree in an inconsistent state. This is typically done by protecting the tree’s data structures with latches (lightweight locks). Log-structured approaches are simpler in this regard, because they do all the merging in the background without interfering with incoming queries and atomically swap old segments for new segments from time to time.
B-tree optimizations
As B-trees have been around for so long, it’s not surprising that many optimizations have been developed over the years. To mention just a few:
- Instead of overwriting pages and maintaining a WAL for crash recovery, some databases (like LMDB) use a copy-on-write scheme. A modified page is written to a different location, and a new version of the parent pages in the tree is created, pointing at the new location. This approach is also useful for concurrency control,
- We can save space in pages by not storing the entire key, but abbreviating it. Especially in pages on the interior of the tree, keys only need to provide enough information to act as boundaries between key ranges. Packing more keys into a page allows the tree to have a higher branching factor, and thus fewer levels.
- In general, pages can be positioned anywhere on disk; there is nothing requiring pages with nearby key ranges to be nearby on disk. If a query needs to scan over a large part of the key range in sorted order, that page-by-page layout can be inefficient, because a disk seek may be required for every page that is read. Many B-tree implementations therefore try to lay out the tree so that leaf pages appear in sequential order on disk. However, it’s difficult to maintain that order as the tree grows. By contrast, since LSM-trees rewrite large segments of the storage in one go during merging, it’s easier for them to keep sequential keys close to each other on disk.
- Additional pointers have been added to the tree. For example, each leaf page may have references to its sibling pages to the left and right, which allows scanning keys in order without jumping back to parent pages.
- B-tree variants such as fractal trees borrow some log-structured ideas to reduce disk seeks (and they have nothing to do with fractals).
MySQL索引实现
在MySQL中,索引属于存储引擎级别的概念,不同存储引擎对索引的实现方式是不同的,本文主要讨论MyISAM和InnoDB两个存储引擎的索引实现方式。
MyISAM索引实现
MyISAM引擎使用B+Tree作为索引结构,叶子节点的data域存放的是数据记录的地址。下图是MyISAM索引的原理图:
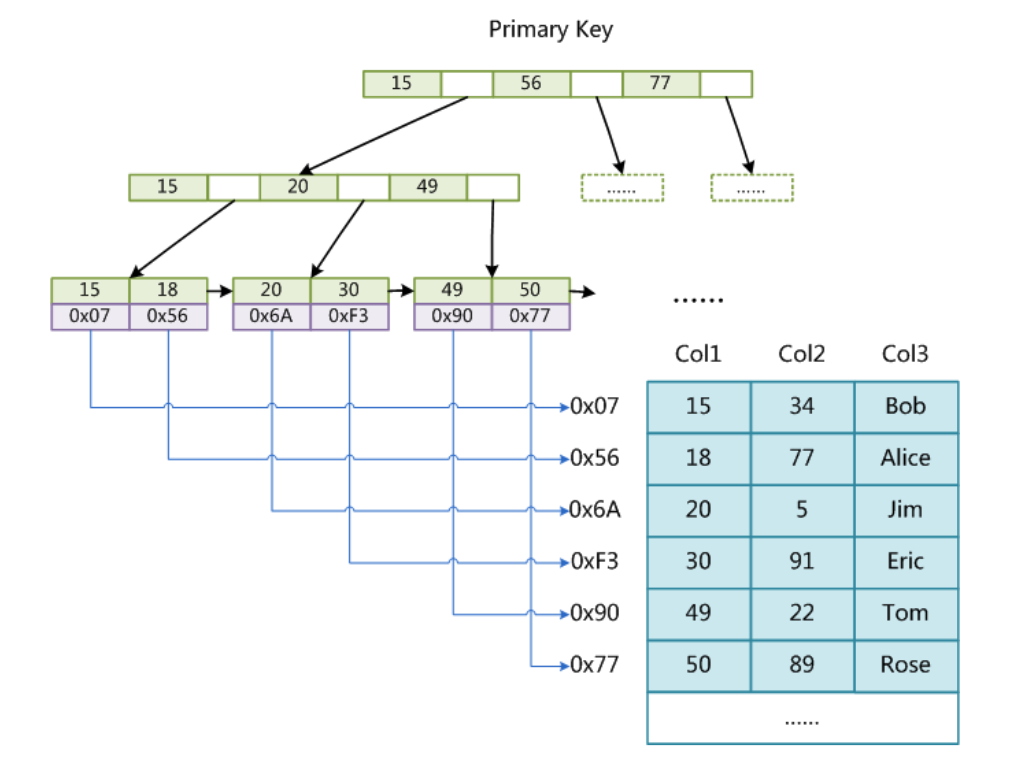
这里设表一共有三列,假设我们以Col1为主键,则上图是一个MyISAM表的主索引(Primary Index)示意。可以看出MyISAM的索引文件仅仅保存数据记录的地址。
在MyISAM中,主索引和**辅助索引(Secondary Index)**在结构上没有任何区别,只是主索引要求key是唯一的,而辅助索引的key可以重复。如果我们在Col2上建立一个辅助索引,则此索引的结构如下图所示:
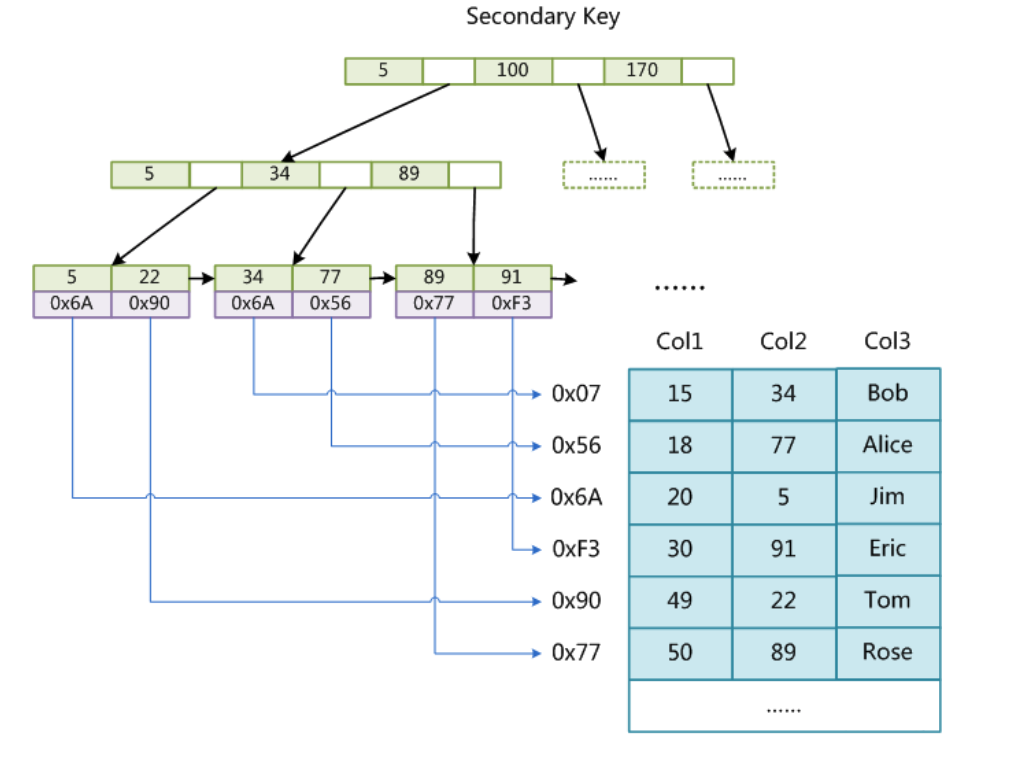
同样也是一颗B+Tree,data域保存数据记录的地址。因此,MyISAM中索引检索的算法为首先按照B+Tree搜索算法搜索索引,如果指定的Key存在,则取出其data域的值,然后以data域的值为地址,读取相应数据记录。
MyISAM的索引方式也叫做**“非聚集”的(非聚集索引,Non-clustered Index),之所以这么称呼是为了与InnoDB的聚集索引(Clustered Index)**区分。
InnoDB索引实现
虽然InnoDB也使用B+Tree作为索引结构,但具体实现方式却与MyISAM截然不同。
第一个重大区别是InnoDB的数据文件本身就是索引文件。从上文知道,MyISAM索引文件和数据文件是分离的,索引文件仅保存数据记录的地址。而在InnoDB中,表数据文件本身就是按B+Tree组织的一个索引结构,这棵树的叶节点data域保存了完整的数据记录。这个索引的key是数据表的主键,因此InnoDB表数据文件本身就是主索引(Primary Index)。
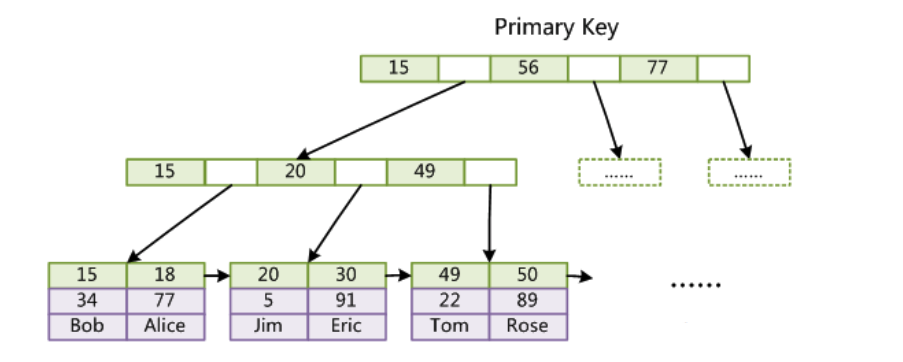
上图是InnoDB主索引(同时也是数据文件)的示意图,可以看到叶节点包含了完整的数据记录。这种索引叫做聚集索引(clustered index)。
因为InnoDB的数据文件本身要按主键聚集,所以InnoDB要求表必须有主键(MyISAM可以没有),如果没有显式指定,则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键,如果不存在这种列,则MySQL自动为InnoDB表生成一个隐含字段作为主键,这个字段长度为6个字节,类型为长整形。
这其实解释了中InnoDB为engine 的表,非常建议创建一个auto increment 的primary key,而不是只设置包含unique属性的column(or),比如 promo_usage_tab
| Field | Type | Key / Index | Description |
|---|---|---|---|
| order_id | bigint(20) NOT NULL | unique | |
| promo_id | bigint(20) unsigned NOT NULL | ||
| user_id | bigint(20) NOT NULL | ||
| shop_id | bigint(20) NOT NULL |
因为 order_id 并不是连续的(显然因为不是每一个order都享受了promotion),
第二个与MyISAM索引的不同是,InnoDB的辅助索引data域存储相应记录主键的值而不是地址。换句话说,InnoDB的所有辅助索引都引用主键作为data域。例如,下图为定义在Col3上的一个辅助索引:
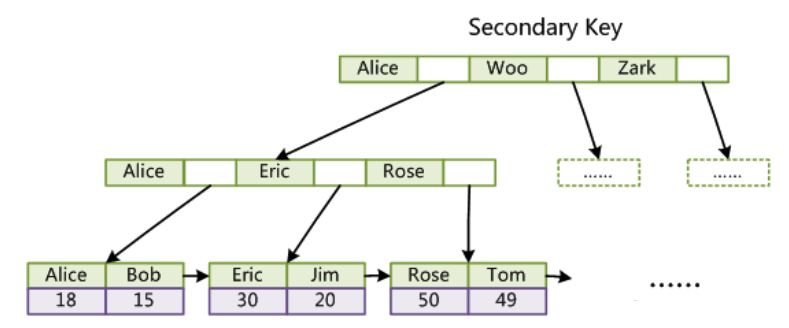
这里以英文字符的ASCII码作为比较准则。聚集索引这种实现方式使得按主键的搜索十分高效,但是辅助索引搜索需要检索两遍索引:首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录。
了解不同存储引擎的索引实现方式对于正确使用和优化索引都非常有帮助,例如知道了InnoDB的索引实现后,就很容易明白为什么不建议使用过长的字段作为主键,因为所有辅助索引都引用主索引,过长的主索引会令辅助索引变得过大。再例如,用非单调的字段作为主键在InnoDB中不是个好主意,因为InnoDB数据文件本身是一颗B+Tree,非单调的主键会造成在插入新记录时数据文件为了维持B+Tree的特性而频繁的分裂调整,十分低效,而使用自增字段作为主键则是一个很好的选择。
Reference
-
Designing Data Intensive Applications
-
数据库索引为什么使用B+树? - https://www.jianshu.com/p/4dbbaaa200c4