背景

在了解赫夫曼树之前，我们首先先介绍一些基础概念。

路径

路径是指在一棵树中，从一个节点到另一个节点之间的分支构成的通路。

如从节点8到节点1的路径如下图所示：

路径长度

路径长度指的是路径上分支的数目，在上图中，路径长度为2。

结点的度

结点的度指的是二叉树结点的分支数目，如果某个结点没有孩子结点，即没有分支，那么它的度是0；如果有一个孩子结点，那么它的度数是1；如果既有左孩子也有右孩子，那么这个结点的度是2。

节点的权

节点的权指的是为树中的每一个节点赋予的一个非负的值，如上图中每一个节点中的值就是对应节点的权。

节点的带权路径长度

节点的带权路径长度指的是从根节点到该节点之间的路径长度与该节点权的乘积：如上图中，对于1节点的带权路径长度为：2。

树的带权路径长度

树的带权路径长度指的是所有叶子节点的带权路径长度之和。

扩充二叉树

对于一颗已有的二叉树，如果我们为它添加一系列新结点，使得它原有的所有结点的度都为2，那么我们就得到了一颗扩充二叉树，如下图所示：

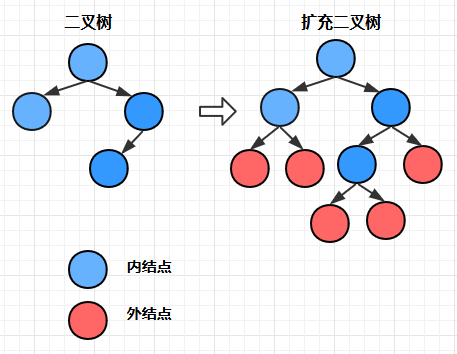
其中原有的结点叫做内结点（非叶子结点），新增的结点叫做外结点（叶子结点）。

我们可以得出：外结点数 = 内结点数 + 1

并进一步得出：总结点数 = 2 × 外结点数 -1

扩充二叉树，构成了赫夫曼树的基本形态，而上面的公式，也是我们构建赫夫曼树的依据之一。

赫夫曼树的外结点和内结点

赫夫曼树的外结点和内结点的性质区别：外节点是携带了关键数据的结点，而内部结点没有携带这种数据，只作为导向最终的外结点所走的路径而使用。

正因如此，我们的关注点最后是落在赫夫曼树的外结点上，而不是内结点。

带权路径长度（WPL）

让我们思考一下：在一颗在外结点上存储了数据的扩充二叉树中进行查找时，数据结点怎么分布才能尽可能减少查找的开销呢？这里我们再加上一个前提：不同的数据结点搜索的频率（或概率）是不一致的。

显然，我们大致的思路是：如果一个数据结点搜索频率越高，就让它分布在离根结点越近的地方，也即从根结点走到该结点经过的路径长度越短。这样就能从整体上优化整颗树的性能。

频率是个细化的量，这里我们用一个更加标准的一个词描述它——“权值”。

综上，我们为扩充二叉树的外结点（叶子结点）定义两条属性： 权值（w）和路径长度（l）。同时规定**带权路径长度（WPL）**为扩充二叉树的外结点的权值和路径长度乘积之和：

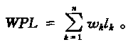
哈夫曼树（最优二叉树，Huffman Tree）

由n个权值构造一颗有n个叶子结点的二叉树，则其中带权路径长度WPL最小的二叉树，就是哈夫曼树（Huffman Tree）****，或者叫做最优二叉树**。

例子

例如下图中对a, b, c：

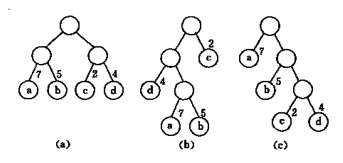
对a: WPL = 7×2 + 5×2 + 2×2 + 4×2 = 36；
对b: WPL = 7×3 + 5×3 + 2×1 + 4×2 = 46;
对c: WPL = 7×1 + 5×2 + 2×3 + 4×3 = 35;

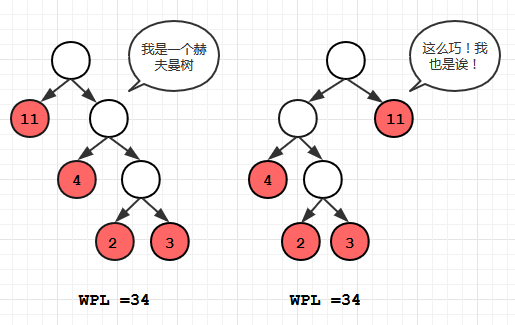
c中WPL最小，可以验证，它就是哈夫曼树，而a和b都不是哈夫曼树。

对于同一组权值的叶结点，构成的哈夫曼树可以有多种形态，但是最小WPL值是唯一的。

赫夫曼树的构建

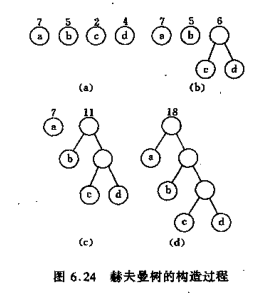
构建过程分四步：

根据给定的n个权值{w1, w2, w3 … wn }构成n棵二叉树的集合，每棵二叉树都只包含一个结点；
在上面的二叉树中选出两颗根结点权值最小的树，同时另外取一个新的结点作为这两颗树的根结点，设新节点的权值为两颗权值最小的树的权值和，将得到的这颗树也加入到树的集合中；
在2操作后，从集合中删除权值最小的那两颗树
重复2和3，直到集合中的树只剩下一棵为止，剩下的这颗树就是我们要求得的赫夫曼树。

如下图所示：

哈夫曼编码（Huffman Coding）

哈夫曼编码是哈夫曼树的一个应用。

哈夫曼编码（Huffman Coding）是一种编码方式，也称为“赫夫曼编码”，是David A. Huffman1952年发明的一种构建极小多余编码的方法。在计算机数据处理中，霍夫曼编码使用变长编码表对源符号进行编码，出现频率较高的源符号采用较短的编码，出现频率较低的符号采用较长的编码，使编码之后的字符串字符串的平均长度、期望值降低，以达到无损压缩数据的目的。举个例子，现在我们有一字符串：

this is an example of a huffman tree

这串字符串有36个字符，如果按普通方式存储这串字符串，每个字符占据1个字节，则共需要36 * 1 * 8 = 288bit。经过分析我们发现，这串字符串中各字母出现的频率不同，如果我们能够按如下编码：

字母	频率	编码	字母	频率	编码
space	7	111	s	2	1011
a	4	010	t	2	0110
e	4	000	l	1	11001
f	3	1101	o	1	00110
h	2	1010	p	1	10011
i	2	1000	r	1	11000
m	2	0111	u	1	00111
n	2	0010	x	1	10010

编码这串字符串，只需要： (7+4+4)x3 + (3+2+2+2+2+2+2)x4 + (1+1+1+1+1+1)x 5 = 45+60+30 = 135bit 编码这串字符串只需要135bit！单单这串字符串，就压缩了288-135 = 153bit。

那么，我们如何获取每个字符串的编码呢？这就需要哈夫曼树了。源字符编码的长短取决于其出现的频率，我们把源字符出现的频率定义为该字符的权值。

Reference

【算法】赫夫曼树（Huffman）的构建和应用（编码、译码） - https://www.cnblogs.com/penghuwan/p/8308324.html
数据结构和算法——Huffman树和Huffman编码 - https://blog.csdn.net/google19890102/article/details/54848262
1. 数据结构 - 哈夫曼树 - https://www.jianshu.com/p/95fba425be44

【Data Structure】哈夫曼树（Huffman Tree）

背景

路径