查找是在大量的信息中寻找一个特定的信息元素,在计算机应用中,查找是常用的基本运算,例如编译程序中符号表的查找。
顺序查找
顺序查找适合于存储结构为顺序存储或链接存储的线性表。
基本思想
顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
复杂度分析
查找成功时的平均查找长度为:(假设每个数据元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
当查找不成功时,需要n+1次比较,时间复杂度为O(n);
所以,顺序查找的时间复杂度为O(n)。
二分查找
说明:元素必须是有序的,如果是无序的,则要先进行排序操作。
基本思想:也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
复杂度分析:最坏情况下,关键词比较次数为$log_2(n+1)$,且期望时间复杂度为$O(log_2n)$;
注:折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用。——《大话数据结构》
特殊的二分查找
插值查找
在介绍插值查找之前,首先考虑一个新问题,为什么上述算法一定要是折半,而不是折四分之一或者折更多呢?
打个比方,在英文字典里面查“apple”,你下意识翻开字典是翻前面的书页还是后面的书页呢?如果再让你查“zoo”,你又怎么查?很显然,这里你绝对不会是从中间开始查起,而是有一定目的的往前或往后翻。
同样的,比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5, 我们自然会考虑从数组下标较小的开始查找。
经过以上分析,折半查找这种查找方式,不是自适应的(也就是说是傻瓜式的)。二分查找中查找点计算如下:
mid=(low+high)/2, 即mid=low+1/2*(high-low);
通过类比,我们可以将查找的点改进为如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low)
也就是将上述的比例参数1/2改进为自适应的,根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数。
**基本思想:**基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。当然,差值查找也属于有序查找。
注:对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
复杂度分析:查找成功或者失败的时间复杂度均为$O(log_2(log_2n))$。
斐波那契查找
在介绍斐波那契查找算法之前,我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。
黄金分割
黄金比例又称黄金分割,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1:0.618或1.618:1。
0.618被公认为最具有审美意义的比例数字,这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。
大家记不记得斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….(从第三个数开始,后边每一个数都是前两个数的和)。然后我们会发现,随着斐波那契数列的递增,前后两个数的比值会越来越接近0.618,利用这个特性,我们就可以将黄金比例运用到查找技术中。
斐波那契查找

**基本思想:**也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法。
相对于折半查找,一般将待比较的key值与第mid=(low+high)/2位置的元素比较,比较结果分三种情况:
1)相等,mid位置的元素即为所求
2)>,low=mid+1;
3)<,high=mid-1。
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=F(k)-1;
开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种
1)相等,mid位置的元素即为所求
2)>,low=mid+1,k-=2;
说明:low=mid+1说明待查找的元素在[mid+1,high]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个,所以可以递归的应用斐波那契查找。
3)<,high=mid-1,k-=1。
说明:low=mid+1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个,所以可以递归 的应用斐波那契查找。
复杂度分析:最坏情况下,时间复杂度为$O(log_2n)$,且其期望复杂度也为$O(log_2n)$。
树表查找
最简单的树表查找算法——二叉树搜索算法(Binary Search Tree)
基本思想
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
二叉查找树(Binary Search Tree),也叫二叉搜索树,或称二叉排序树,(Binary Sort Tree)。
二叉查找树是具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树。
二叉查找树性质
对二叉查找树进行中序遍历,即可得到有序的数列。
复杂度分析
它和二分查找一样,插入和查找的时间复杂度均为$O(log_2n)$,但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷。
基于二叉查找树进行优化,进而可以得到其他的树表查找算法,如平衡树、红黑树等高效算法。
多路查找树(muitl-way search tree) - 2 - 3查找树(2-3 Tree)
2 - 3查找树定义
和二叉树不一样,2-3树运行每个节点保存一个或者两个的值。
- 对于2度节点(2-node),包含 1 个值,且只有 2 个子节点;
- 对于3度节点(3-node),包含 2 个值,且只有 3 个子节点。
2 - 3查找树的定义如下:
- 任一节点只能是 2 度节点(2-node)或 3 度节点(3-node),不存在值的数量为 0 的节点。
- 2 度节点(2-node):包含 1 个值,且只有 2 个子节点的节点:
- 左子节点子树中所有节点的值都小于这个2 度节点的值;
- 右子节点子树中所有节点的值都大于等于这个2 度节点的值。
- 3 度节点(3-node):包含 2 个值,且只有 3 个子节点的节点:
- 该节点的左值小于右值;
- 左子节点子树中所有节点的值都小于这个 3 度节点的左值;
- 中子节点子树中所有节点的值都大于等于这个 3 度节点的左值,且小于这个 3 度节点的右值;
- 右子节点子树中所有节点的值都大于这个 3 度节点的右值。
- 2 度节点(2-node):包含 1 个值,且只有 2 个子节点的节点:
- 所有叶子节点都拥有相同的深度(depth),或者说,根节点到每一个为空节点的距离都相同。
- 元素始终保持排序顺序。
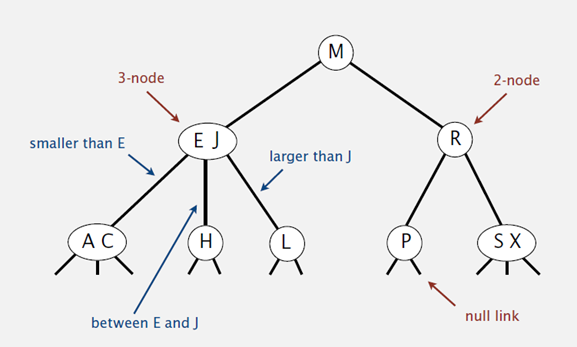
2-3查找树的性质
- 如果中序遍历2-3查找树,就可以得到排好序的序列;
- 在一个完全平衡的2-3查找树中,根节点到每一个为空节点的距离都相同(这也是平衡树中“平衡”一词的概念,根节点到叶节点的最长距离对应于查找算法的最坏情况,而平衡树中根节点到叶节点的距离都一样,意味着在最坏情况下,时间复杂度也为$log_2N$)。
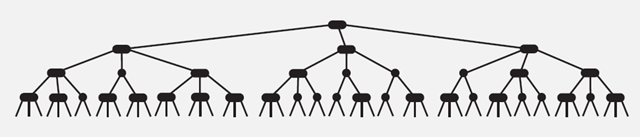
性能分析
2-3树的查找效率与树的高度是息息相关的。
- 在最坏的情况下,也就是所有的节点都是2-node节点,查找效率为$log_2N$;
- 在最好的情况下,所有的节点都是3-node节点,查找效率为$log_3N$约等于$0.631log_2N$;
距离来说,对于1百万个节点的2-3树,树的高度为12-20之间,对于10亿个节点的2-3树,树的高度为18-30之间。
对于插入来说,只需要常数次操作即可完成,因为他只需要修改与该节点关联的节点即可,不需要检查其他节点,所以效率和查找类似。下面是2-3查找树的效率:
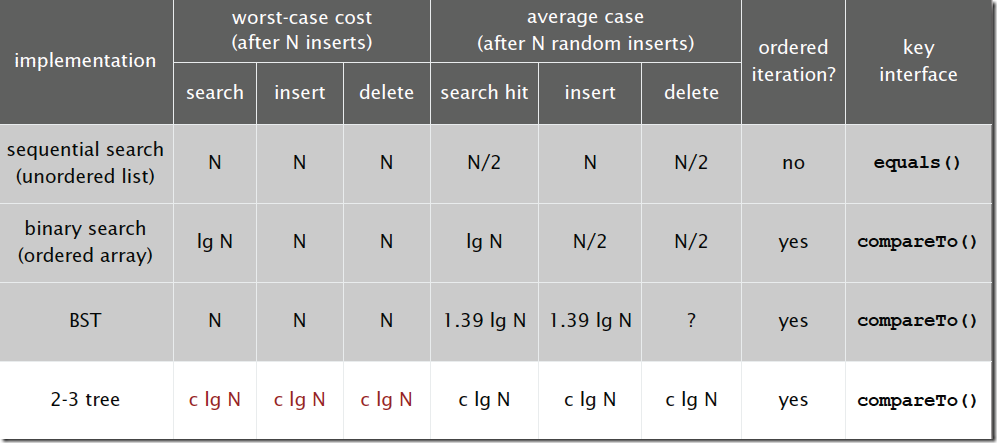
多路查找树(muitl-way search tree) - 红黑树(Red-Black Tree)
多路查找树(muitl-way search tree) - B树(B - Tree)
树表查找总结
二叉查找树平均查找性能不错,为 $log_2N$ ,但是最坏情况会退化为O(n)。在二叉查找树的基础上进行优化,我们可以使用平衡查找树。平衡查找树中的2-3查找树,这种数据结构在插入之后能够进行自平衡操作,从而保证了树的高度在一定的范围内进而能够保证最坏情况下的时间复杂度。但是2-3查找树实现起来比较困难,红黑树是2-3树的一种简单高效的实现,他巧妙地使用颜色标记来替代2-3树中比较难处理的3-node节点问题。红黑树是一种比较高效的平衡查找树,应用非常广泛,很多编程语言的内部实现都或多或少的采用了红黑树。
除此之外,2-3查找树的另一个扩展——B/B+平衡树,在文件系统和数据库系统中有着广泛的应用。
分块查找
分块查找又称索引顺序查找,它是顺序查找的一种改进方法。
算法思想
顺序查找和二分查找的结合。
将n个数据元素"按块有序"划分为m块(m ≤ n)。每一块中的结点不必有序,但块与块之间必须"按块有序";即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字;而第2块中任一元素又都必须小于第3块中的任一元素,……
算法流程
- 先选取各块中的最大关键字构成一个索引表;
- 查找分两个部分:先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;然后,在已确定的块中用顺序法进行查找。
效率
时间复杂度:介于 O(n) 和 $log_2n$ 之间。
哈希查找
什么是哈希表(Hash)?
我们使用一个下标范围比较大的数组来存储元素。可以设计一个函数(哈希函数, 也叫做散列函数),使得每个元素的关键字都与一个函数值(即数组下标)相对应,于是用这个数组单元来存储这个元素;也可以简单的理解为,按照关键字为每一个元素"分类",然后将这个元素存储在相应"类"所对应的地方。但是,不能够保证每个元素的关键字与函数值是一一对应的,因此极有可能出现对于不同的元素,却计算出了相同的函数值,这样就产生了"冲突",换句话说,就是把不同的元素分在了相同的"类"之中。后面我们将看到一种解决"冲突"的简便做法。
总的来说,“直接定址"与"解决冲突"是哈希表的两大特点。
什么是哈希函数?
哈希函数的规则是:通过某种转换关系,使关键字适度的分散到指定大小的的顺序结构中,越分散,则以后查找的时间复杂度越小,空间复杂度越高。
算法思想
哈希的思路很简单,如果所有的键都是整数,那么就可以使用一个简单的无序数组来实现:将键作为索引,值即为其对应的值,这样就可以快速访问任意键的值。这是对于简单的键的情况,我们将其扩展到可以处理更加复杂的类型的键。
算法流程
- 用给定的哈希函数构造哈希表;
- 根据选择的冲突处理方法解决地址冲突。常见的解决冲突的方法:拉链法和线性探测法。
- 在哈希表的基础上执行哈希查找。
哈希表是一个在时间和空间上做出权衡的经典例子。如果没有内存限制,那么可以直接将键作为数组的索引。那么所有的查找时间复杂度为O(1);如果没有时间限制,那么我们可以使用无序数组并进行顺序查找,这样只需要很少的内存。哈希表使用了适度的时间和空间来在这两个极端之间找到了平衡。只需要调整哈希函数算法即可在时间和空间上做出取舍。
复杂度分析
单纯论查找复杂度:对于无冲突的Hash表而言,查找复杂度为O(1)(注意,在查找之前我们需要构建相应的Hash表)。
Hash是一种典型以空间换时间的算法,比如原来一个长度为100的数组,对其查找,只需要遍历且匹配相应记录即可,从空间复杂度上来看,假如数组存储的是byte类型数据,那么该数组占用100byte空间。现在我们采用Hash算法,我们前面说的Hash必须有一个规则,约束键与存储位置的关系,那么就需要一个固定长度的hash表,此时,仍然是100byte的数组,假设我们需要的100byte用来记录键与位置的关系,那么总的空间为200byte,而且用于记录规则的表大小会根据规则,大小可能是不定的。
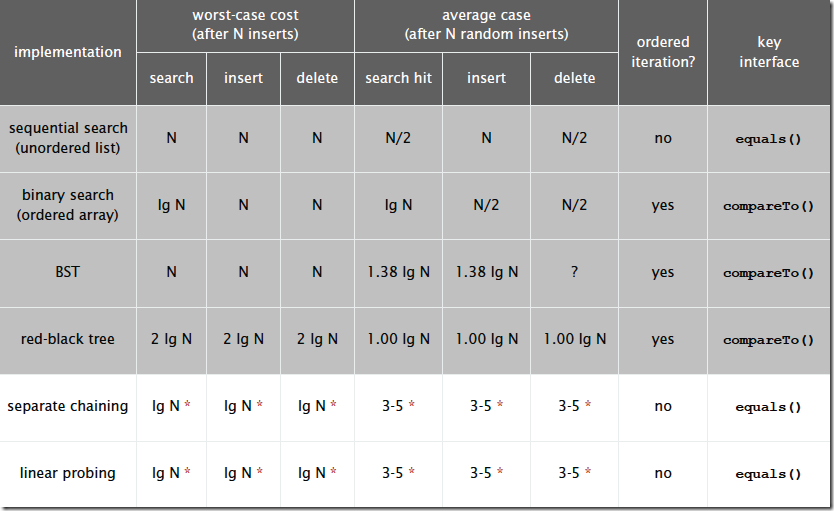
Hash算法和其他查找算法的性能对比: