线索二叉树(Threaded Binary Tree)
通过观察二叉链表,我们发现,不管二叉树的形态如何,空链域的个数总是多于非空链域的个数。准确的说,有n个结点的二叉链表共有2n个链域,非空链域为n-1个,但其中的空链域却有n+1个。如下图所示。
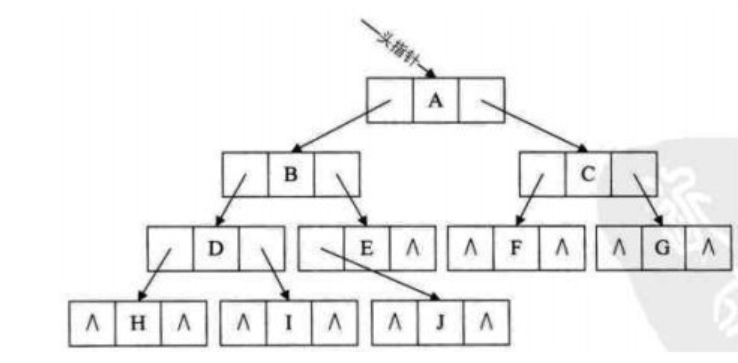
这样,我们可以通过利用二叉链表中的空指针域,来存放指向结点在某种遍历次序下的前趋和后继结点的指针(这种附加的指针称为 “线索” ),这种加上了线索的二叉链表称为线索链表(Threaded Linked List),相应的二叉树称为线索二叉树(Threaded Binary Tree)。
为什么要建立线索二叉树
有了二叉树不就足够了吗?那为什么还要弄个线索二叉树出来呢?
在原来的二叉链表中,如果想查找一个结点的左、右孩子节点非常容易。比如,在上图中,我们想查找节点B的左、右孩子节点(分别是节点D和节点E),我们只需要根据节点B中记录的两个链域,即可找到。
可是,如果要找该结点的前趋和后继结点呢?
这就变得非常困难。所以,为了实现这个常见的需求,我们要在每个结点中增加两个指针域,来分别存放遍历时得到的前趋(successor)结点和后继(predecessor)结点,这样就可以通过该指针直接或间接访问到其前趋和后继结点。
根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。比如,若对二叉树进行中序遍历,则所得的线索二叉树称为中序线索二叉树,线索链表称为为中序线索链表。
举例
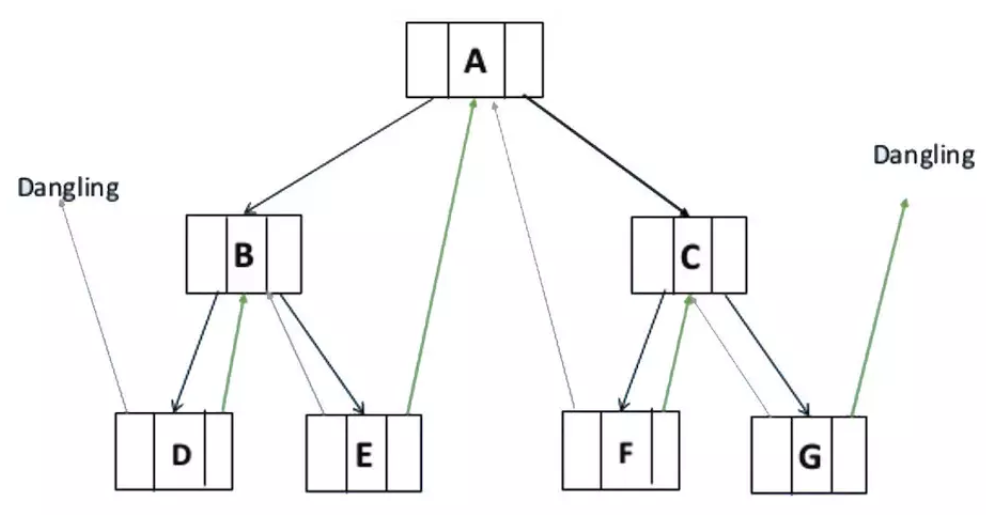
如图,以中序二叉树为例,我们可以把这颗二叉树中所有结点的空左指针域(lchild域),改为指向当前结点的前驱结点(灰色箭头表示),把空右指针域(rchild域),改为指向当前结点的后继结点(绿色箭头表示)。我们把指向前驱结点和后继结点的指针叫做线索 ,下图中这个加上线索的二叉树就称之为线索二叉树。
注意,对这个二叉树采用中序遍历时,访问节点的次序为:D B E A F C G。
线索二叉树结点结构
如果只是在原二叉树的基础上利用空结点,那么就存在着这么一个问题:我们如何知道某一结点的lchild是指向他的左孩子还是指向前驱结点?rchild是指向右孩子还是后继结点?显然我们要对他的指向增设标志来加以区分。
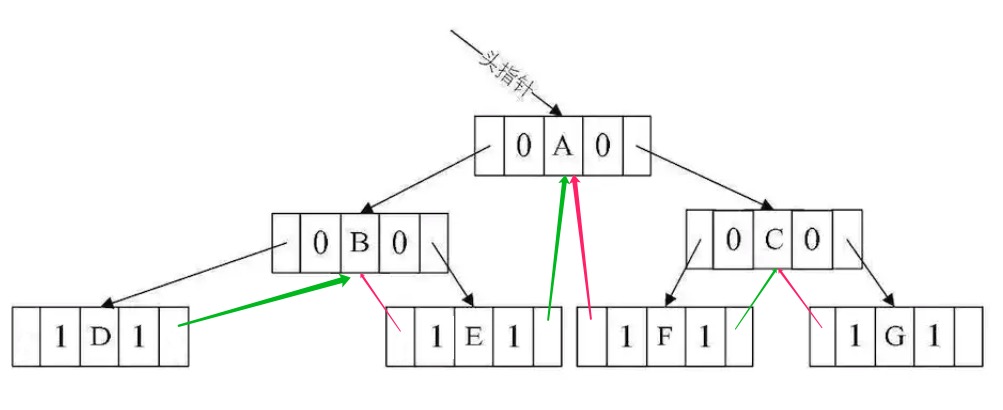
因此,我们在每一个结点都增设两个标志域LTag和RTag,它们只存放0或1的布尔型变量,占用的空间很小。于是结点的结构如下图所示。

其中:
- LTag为0时,表示该一结点的lchild指向该结点的左孩子,为1时指向该结点的前驱结点;
- RTag为0时,表示该一结点的rchild指向该结点的右孩子,为1时指向该结点的后继结点。
因此实际的中序线索链表如下所示:
二叉树的线索化
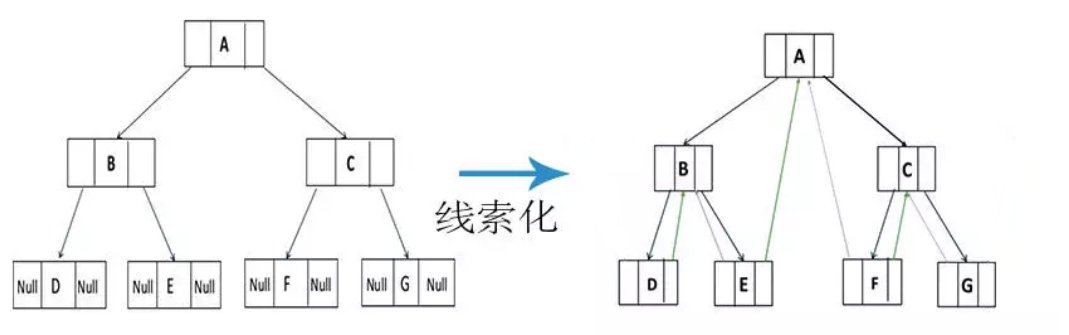
对普通二叉树以某种次序遍历使其成为线索二叉树的过程就叫做线索化。因为前驱和后继结点只有在二叉树的遍历过程中才能得到,所以线索化的具体过程就是在二叉树的遍历中修改空指针。
增设头结点
线索化后的二叉树,就如同操作一个双向链表。于是我们想到为二叉树增设一个头结点,这样就和双向链表一样,即能够从第一个结点正向开始遍历,也可以从最后一个结点逆向遍历。我们将其称之为双向线索链表。
这样定义的好处是既可以从第一个结点起顺后继进行遍历,也可以从最后一个结点起顺前驱进行遍历。
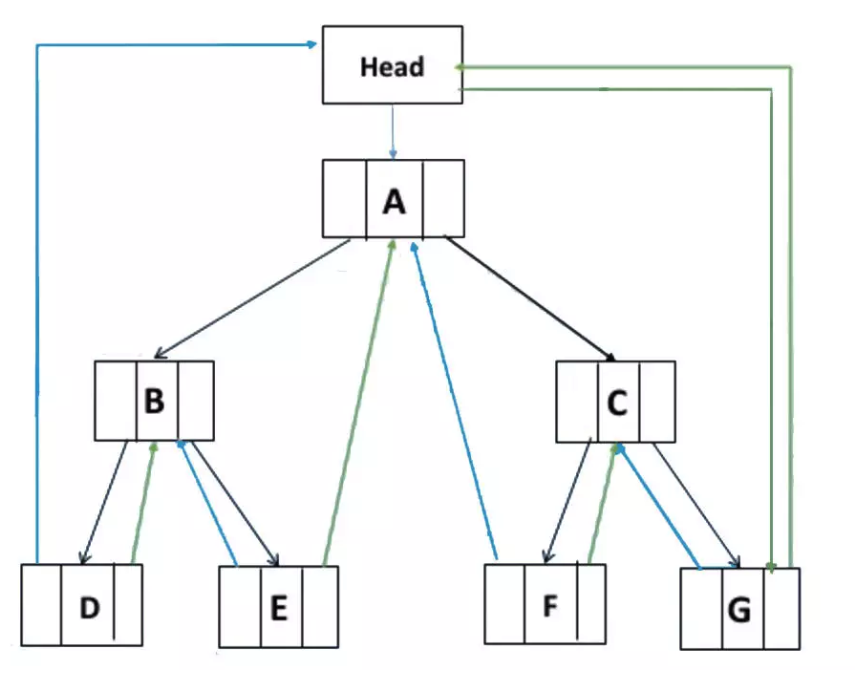
如上图,在线索二叉链表上添加一个head结点,并令其lchild域的指针指向二叉树的根结点(A),其rchild域的指针指向中序遍历访问的最后一个结点(G)。同样地,二叉树中序序列的第一个结点中,lchild域指针指向头结点,中序序列的最后一个结点rchild域指针也指向头结点。
于是从头结点开始,我们既可以从第一个结点顺后继结点遍历,也可以从最后一个结点起顺前驱遍历。就和双链表一样。
Reference
- 数据结构和算法系列15 线索二叉树 - https://www.cnblogs.com/mcgrady/p/3320413.html
- 线索二叉树 - https://www.cnblogs.com/zhuyf87/archive/2012/11/03/2752722.html
- 理解线索二叉树 - https://www.jianshu.com/p/deb1d2f2549a