常用数据结构的时间复杂度
| Data Structure | Add | Find | Delete | GetByIndex |
|---|---|---|---|---|
| Array (T[]) | O(n) | O(n) | O(n) | O(1) |
| Linked list (LinkedList) | O(1) | O(n) | O(n) | O(n) |
| Resizable array list (List) | O(1) | O(n) | O(n) | O(1) |
| Stack (Stack) | O(1) | - | O(1) | - |
| Queue (Queue) | O(1) | - | O(1) | - |
| Hash table (Dictionary) | O(1) | O(1) | O(1) | - |
| Tree-based dictionary (SortedDictionary<K,T>) | O(log n) | O(log n) | O(log n) | - |
| Hash table based set (HashSet) | O(1) | O(1) | O(1) | - |
| Tree based set (SortedSet) | O(log n) | O(log n) | O(log n) | - |
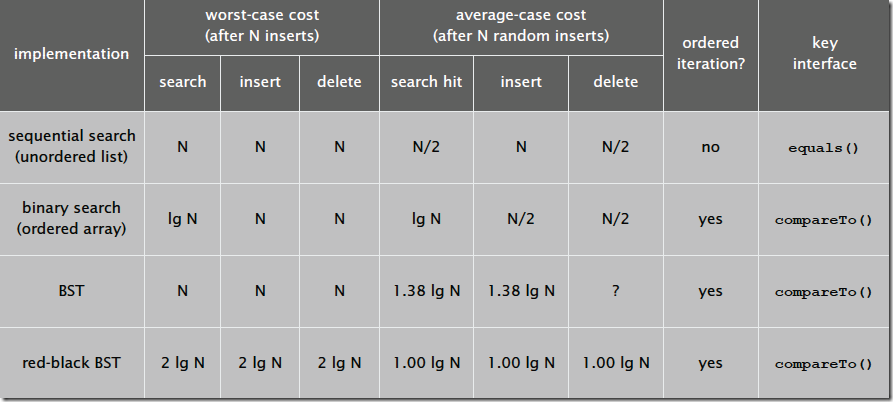
如何选择数据结构
- Array (T[]):当元素的数量是固定的,并且需要使用下标时。
- Linked list (LinkedList):当元素需要能够在列表的两端添加时。否则使用 List。
- Resizable array list (List):当元素的数量不是固定的,并且需要使用下标时。
- Stack (Stack):当需要实现 LIFO(Last In First Out)时。
- Queue (Queue):当需要实现 FIFO(First In First Out)时。
- Hash table (Dictionary<K,T>):当需要使用键值对(Key-Value)来快速添加和查找,并且元素没有特定的顺序时。
- Tree-based dictionary (SortedDictionary<K,T>):当需要使用价值对(Key-Value)来快速添加和查找,并且元素根据 Key 来排序时。
- Hash table based set (HashSet):当需要保存一组唯一的值,并且元素没有特定顺序时。
- Tree based set (SortedSet):当需要保存一组唯一的值,并且元素需要排序时。
各种数据结构
数组(Array)
在计算机程序设计中,数组(Array)是最简单的而且应用最广泛的数据结构之一。在任何编程语言中,数组都有一些共性:
- 数组中的内容是使用连续的内存(Contiguous Memory)来存储的。
- 数组中的所有元素必须是相同的类型,或者类型的衍生类型。因此数组又被认为是同质数据结构(Homegeneous Data Structures)。
- 数组的元素可以直接被访问。比如你需要访问数组的第 i 个元素,则可以直接使用 arrayName[i] 来访问。
对于数组的常规操作包括:
- 分配空间(Allocation)
- 数据访问(Accessing)
链表(LinkedList)
在链表(Linked List)中,每一个元素都指向下一个元素,以此来形成了一个链(chain)。
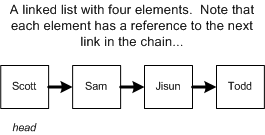
在创建一个链表时,我们仅需持有头节点 head 的引用,通过逐个遍历下一个节点 next 即可找到所有的节点。
查找元素
对于查找元素,链表与数组有着同样的线性运行时间 O(n)。例如在上图中,如果我们要查找 Sam 节点,则必须从头节点 Scott 开始查找,逐个遍历下一个节点直到找到 Sam。
删除元素
同样,从链表中删除一个节点的渐进时间也是线性的O(n)。因为在删除之前我们仍然需要从 head 开始遍历以找到需要被删除的节点。而删除操作本身则变得简单,即让被删除节点的左节点的 next 指针指向其右节点。下图展示了如何删除一个节点。
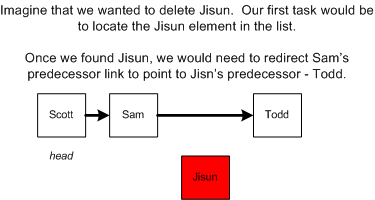
插入元素
向链表中插入一个新的节点的渐进时间取决于链表是否是有序的。如果链表不需要保持顺序,则插入操作就是常量时间O(1),可以在链表的头部或尾部添加新的节点。
而如果需要保持链表的顺序结构,则需要查找到新节点被插入的位置,这使得需要从链表的头部 head 开始逐个遍历,结果就是操作变成了O(n)。下图展示了插入节点的示例。
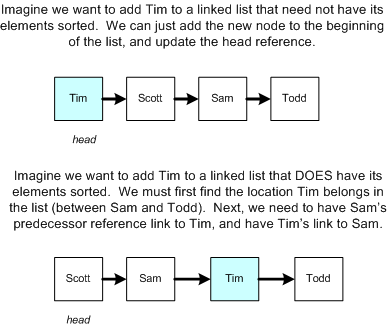
链表与数组
链表与数组的不同之处在于,数组的中的内容在内存中时连续排列的,可以通过下标来访问,而链表中内容的顺序则是由各对象的指针所决定,这就决定了其内容的排列不一定是连续的,所以不能通过下标来访问。如果需要更快速的访问操作,使用数组可能是更好的选择。
使用链表的最主要的优势就是,向链表中插入或删除节点无需调整结构的容量。而相反,对于数组来说容量始终是固定的,如果需要存放更多的数据,则需要调整数组的容量,这就会发生新建数组、数据拷贝等一系列复杂且影响效率的操作。
链表的另一个优点就是特别适合以排序的顺序动态的添加新元素。如果要在数组的中间的某个位置添加新元素,不仅要移动所有其余的元素,甚至还有可能需要重新调整容量。
所以总结来说,数组适合数据的数量是有上限的情况,而链表适合元素数量不固定的情况。
队列(Queue)
队列(Queue)是一个先进先出顺序(FIFO)的数据结构。
Queue 内部建立了一个存放 T 对象的环形数组,并通过 head 和 tail 变量来指向该数组的头和尾。
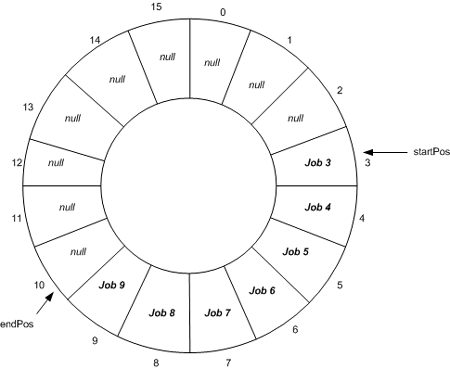
栈(Stack)
栈(Stack)是一个后进先出顺序(LIFO)的数据结构,其提供 Push 和 Pop 方法来实现对 Stack元素的存取。
Stack中存储的元素可以通过一个垂直的集合来形象的表示。当新的元素压入栈中(Push)时,新元素被放到所有其他元素的顶端。当需要弹出栈(Pop)时,元素则被从顶端移除。
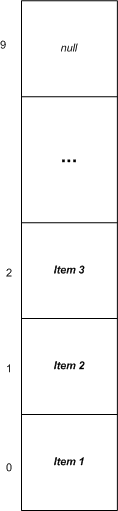
Push 操作的复杂度为 O(1)。如果容量需要被扩展(前提是栈通过数组来实现),则 Push 操作的复杂度变为 O(n)。Pop 操作的复杂度始终为 O(1)。
Hashtable
现在假设我们要使用员工的社保号作为唯一标识进行存储。社保号的格式为 DDD-DD-DDDD(D 的范围为数字 0-9)。
如果使用 Array 存储员工信息,要查询社保号为 111-22-3333 的员工,则将会尝试遍历数组的所有位置,即查询操作的时间复杂度为 O(n) 。
如果我们仍然使用 Array 存储员工信息,但是将社保号基于其对应的数字大小进行排序,那么,查询一个指定的社保号操作的时间复杂度为 $O(log_2(n))$ 。
但,我们希望查询操作的时间复杂度为 O(1)。
方案1
一种方案是建立一个大数组,范围从 000-00-0000 到 999-99-9999 。
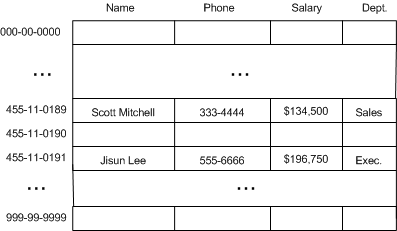
这种方案的缺点是浪费空间。如果我们仅需要存储 1000 个员工的信息,那么仅利用了 0.0001% 的空间。
方案2
第二种方案就是用**哈希函数(Hash Function)**压缩序列。
我们选择使用社保号的后四位作为索引,以减少区间的跨度。这样范围将从 0000 到 9999。
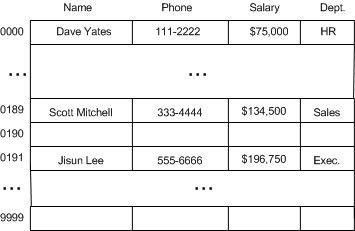
或者,我们也可以采用将 9 位数转换为 4 位数的方式,在数学上,这种方式称为哈希转换(Hashing)。可以将一个数组的索引空间(indexers space)压缩至相应的哈希表(Hash Table)。在上面的例子中,哈希函数的输入为 9 位数的社保号,输出结果为后 4 位。
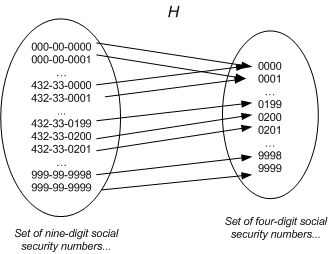
上图中也说明在哈希函数计算中常见的一种行为:哈希冲突(Hash Collisions)。即有可能两个社保号的后 4 位均为 0000。
当要添加新元素到 Hashtable 中时,哈希冲突是导致操作被破坏的一个因素。如果没有冲突发生,则元素被成功插入。如果发生了冲突,则需要判断冲突的原因。因此,哈希冲突提高了操作的代价,Hashtable 的设计目标就是要尽可能减低冲突的发生。
处理哈希冲突的方式有两种:避免和解决,即冲突避免机制(Collision Avoidance)和冲突解决机制(Collision Resolution)。
避免哈希冲突的一个方法就是选择合适的哈希函数。哈希函数中的冲突发生的几率与数据的分布有关。例如,如果社保号的后 4 位是随即分布的,则使用后 4 位数字比较合适。但如果后 4 位是以员工的出生年份来分配的,则显然出生年份不是均匀分布的,则选择后 4 位会造成大量的冲突。我们将这种选择合适的哈希函数的方法称为冲突避免机制(Collision Avoidance)。
在处理冲突时,有很多策略可以实施,这些策略称为冲突解决机制(Collision Resolution)。其中一种方法就是将要插入的元素放到另外一个块空间中,因为相同的哈希位置已经被占用。
通常采用的冲突解决策略为开放寻址法(Open Addressing),所有的元素仍然都存放在哈希表内的数组中。
开放寻址法的最简单的一种实现就是线性探查(Linear Probing),步骤如下:
- 当插入新的元素时,使用哈希函数在哈希表中定位元素位置;
- 检查哈希表中该位置是否已经存在元素。如果该位置内容为空,则插入并返回,否则转向步骤 3。
- 如果该位置为 i,则检查 i+1 是否为空,如果已被占用,则检查 i+2,依此类推,直到找到一个内容为空的位置。
现在如果我们要将五个员工的信息插入到哈希表中:
- Alice (333-33-1234)
- Bob (444-44-1234)
- Cal (555-55-1237)
- Danny (000-00-1235)
- Edward (111-00-1235)
则插入后的哈希表可能如下:
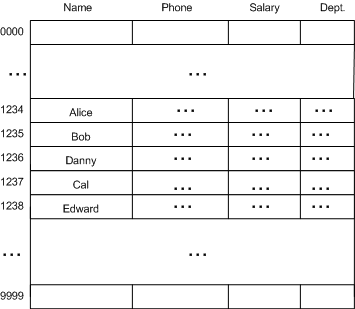
元素的插入过程:
- Alice 的社保号被哈希为 1234,因此存放在位置 1234。
- Bob 的社保号被哈希为 1234,但由于位置 1234 处已经存放 Alice 的信息,则检查下一个位置 1235,1235 为空,则 Bob 的信息就被放到 1235。
- Cal 的社保号被哈希为 1237,1237 位置为空,所以 Cal 就放到 1237 处。
- Danny 的社保号被哈希为 1235,1235 已被占用,则检查 1236 位置是否为空,1236 为空,所以 Danny 就被放到 1236。
- Edward 的社保号被哈希为 1235,1235 已被占用,检查1236,也被占用,再检查1237,直到检查到 1238时,该位置为空,于是 Edward 被放到了1238 位置。
一种改进的方式为二次探查(Quadratic Probing),即每次检查位置空间的步长为平方倍数。也就是说,如果位置 s 被占用,则首先检查 s + 12 处,然后检查s - 12,s + 22,s - 22,s + 32 依此类推,而不是象线性探查那样以 s + 1,s + 2 … 方式增长。尽管如此,二次探查同样也会导致同类哈希聚集问题(Secondary Clustering)。
Reference
- 常用数据结构及复杂度 - https://www.cnblogs.com/gaochundong/p/data_structures_and_asymptotic_analysis.html
- 浅谈算法和数据结构: 十一 哈希表 - https://www.cnblogs.com/yangecnu/p/Introduce-Hashtable.html