Trie树

Trie树，又叫字典树、前缀树（Prefix Tree）、单词查找树或键树，是一种多叉树（k-ary search tree）结构。如下图：

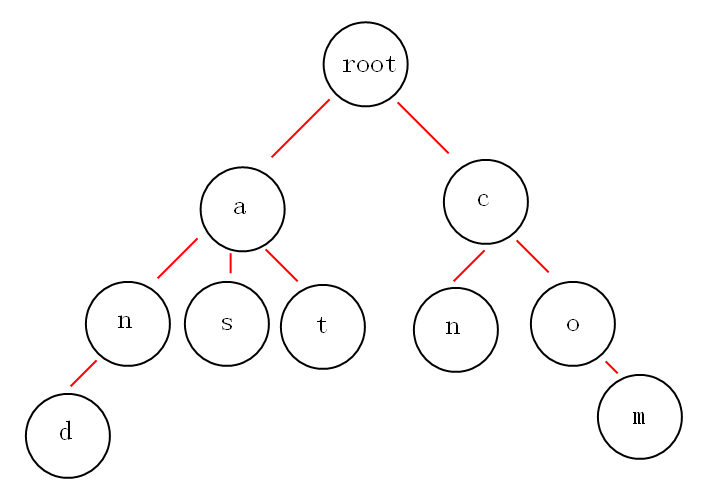
从上图可以归纳出Trie树的基本性质：

根节点不包含字符，除根节点外的每一个子节点都包含一个字符。
从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符互不相同。
通常在实现的时候，会在节点结构中设置一个标志，用来标记该结点处是否构成一个单词（关键字）。

可以看出，Trie树的关键字一般都是字符串，而且Trie树把每个关键字保存在一条路径上，而不是一个结点中。另外，两个有公共前缀的关键字，在Trie树中前缀部分的路径相同，所以Trie树又叫做前缀树（Prefix Tree）。

典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是最大限度地减少无谓的字符串比较，查询效率比较高。

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

搜索 Trie 树的时间复杂度

在 Trie 树中搜索一个字符串，会从根节点出发，沿着某条链路向下逐字比对字符串的每个字符，直到抵达底部的叶子节点才能确认字符串为该词，这种检索方式具有以下两个优点：

公共前缀的词都位于同一个串内，查词范围因此被大幅缩小（比如首字不同的字符串，都会被排除）。
Trie 树实质是一个有限状态自动机（(Definite Automata, DFA），这就意味着从 Trie 树的一个节点（状态）转移到另一个节点（状态）的行为完全由状态转移函数控制，而状态转移函数本质上是一种映射，这意味着：逐字搜索 Trie 树时，从一个字符到下一个字符比对是不需要遍历该节点的所有子节点的。

Trie树的局限性

如前文所讲，Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

假设字符的种数有m个，有若干个长度为n的字符串构成了一个 Trie树，则每个节点的出度为 m（即每个节点的可能子节点数量为m），Trie树的高度为n。很明显我们浪费了大量的空间来存储字符，此时Trie树的最坏空间复杂度为$O(m^n)$。也正由于每个节点的出度为m，所以我们能够沿着树的一个个分支高效的向下逐个字符的查询，而不是遍历所有的字符串来查询，此时Trie树的最坏时间复杂度为O(n)。

这正是空间换时间的体现，也是利用公共前缀降低查询时间开销的体现。

操作

Trie树的插入操作

Trie树的插入操作很简单，其实就是将单词的每个字母逐一插入 Trie树。插入前先看字母对应的节点是否存在，存在则共享该节点，不存在则创建对应的节点。比如要插入新单词cook，就有下面几步：

插入第一个字母 c，发现 root 节点下方存在子节点 c，则共享节点 c
插入第二个字母 o，发现 c 节点下方存在子节点 o，则共享节点 o
插入第三个字母 o，发现 o 节点下方不存在子节点 o，则创建子节点 o
插入第三个字母 k，发现 o 节点下方不存在子节点 k，则创建子节点 k
至此，单词 cook 中所有字母已被插入 Trie树中，然后设置节点 k 中的标志位，标记路径 root->c->o->o->k这条路径上所有节点的字符可以组成一个单词cook

Trie树的查询操作

在 Trie 树中查找一个字符串的时候，比如查找字符串 code，可以将要查找的字符串分割成单个的字符 c，o，d，e，然后从 Trie 树的根节点开始匹配。如图所示，绿色的路径就是在 Trie 树中匹配的路径。

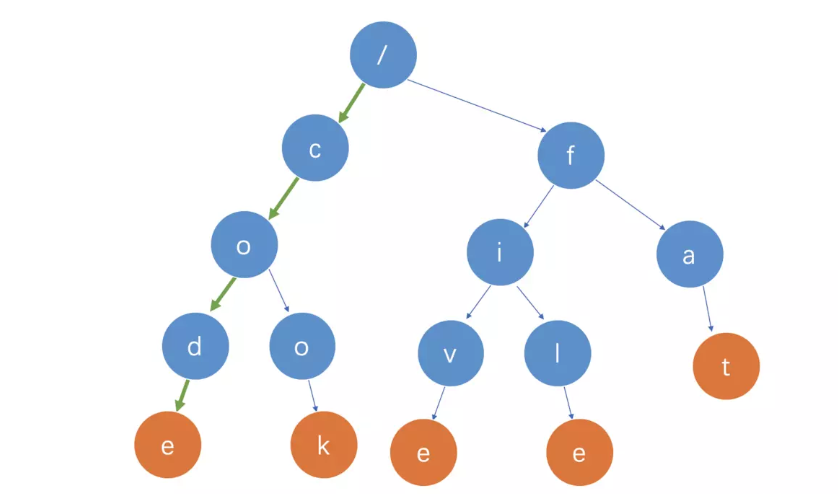
如果要查找的是字符串cod(鳕鱼)呢？还是可以用上面同样的方法，从根节点开始，沿着某条路径来匹配，如图所示，绿色的路径，是字符串cod匹配的路径。但是，路径的最后一个节点「d」并不是橙色的，并不是单词标志位，所以cod字符串不存在。也就是说，cod是某个字符串的前缀子串，但并不能完全匹配任何字符串。

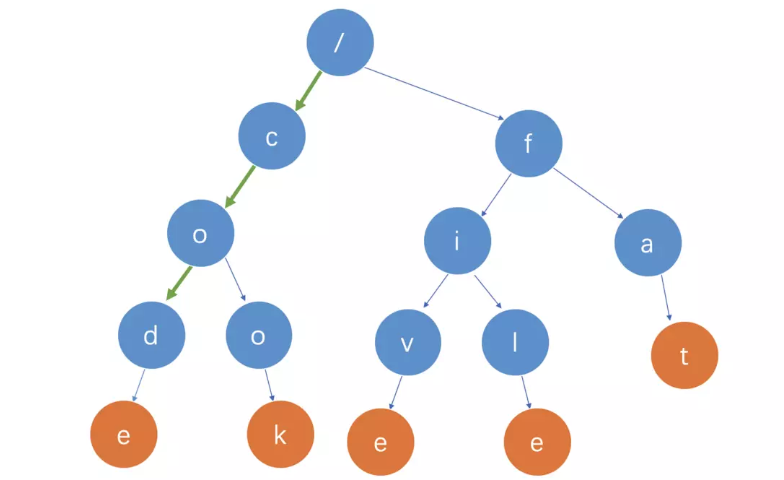
使用范围

既然学Trie树，我们肯定要知道这玩意是用来干嘛的。

字符串检索

给出 N 个单词组成的熟词表，以及一篇全用小写英文书写的文章，按最早出现的顺序写出所有不在熟词表中的生词。

检索/查询功能是Trie树最原始的功能。思路就是从根节点开始一个一个字符进行比较：

如果沿路比较，发现不同的字符，则表示该字符串在集合中不存在。
如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表一个关键字）。

struct trie_node
{
    bool isKey;   // 标记该节点是否代表一个关键字
    trie_node *children[26]; // 各个子节点 
};

词频统计

Trie树常被搜索引擎系统用于文本词频统计。

思路：为了实现词频统计，我们修改了节点结构，用一个整型变量count来计数。对每一个关键字执行插入操作，若已存在，计数加1，若不存在，插入后count置1。

struct trie_node
{
    int count;   // 记录该节点代表的单词的个数
    trie_node *children[26]; // 各个子节点 
};

前缀匹配

如果我想获取所有以"a"开头的字符串，从图中可以很明显的看到是：and,as,at，如果不用trie树，你该怎么做呢？很显然朴素的做法时间复杂度为$O(N^2)$ ，那么用Trie树就不一样了，它可以做到h，h为你检索单词的长度，可以说这是秒杀的效果。

例如：找出一个字符串集合中所有以ab开头的字符串。我们只需要用所有字符串构造一个trie树，然后输出以a->b->开头的路径上的关键字即可。

trie树前缀匹配常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

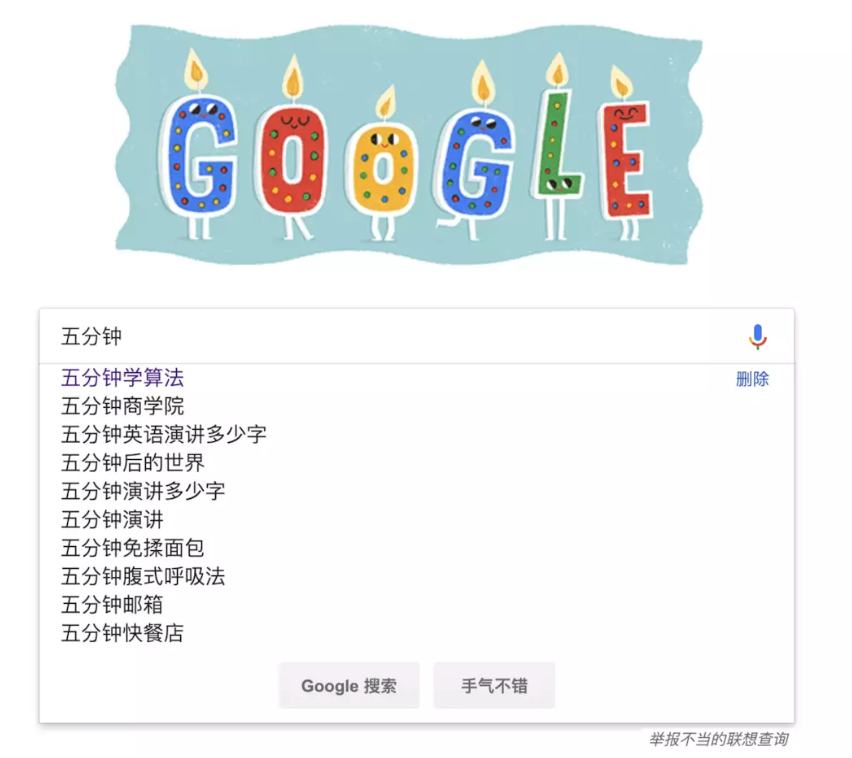
例如：找出一个字符串集合中所有以 五分钟 开头的字符串。我们只需要用所有字符串构造一个 trie树，然后输出以五−>分−>钟开头的路径上的关键字即可。

trie树前缀匹配常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能：

字符串排序

Trie树可以对大量字符串按字典序进行排序，思路也很简单：遍历一次所有关键字，将它们全部插入trie树，树的每个结点的所有儿子很显然地按照字母表排序，然后先序遍历输出Trie树中所有关键字即可。

作为其他数据结构和算法的辅助结构

如后缀树，AC自动机等。

Trie 树的几种实现

Array Trie 树

很多文章里将这种实现称为“标准 Trie 树”，但其实它只是 Trie 众多实现中的一种而已，由于这种实现结构简单，检索效率很好，作为讲解示例很不错，因此特地改称其为“经典 Trie 树”。

abc、d、da、dda 四个字符串构成的 Trie 树，如果是字符串会在节点的尾部进行标记。没有后续字符的 branch 分支指向NULL

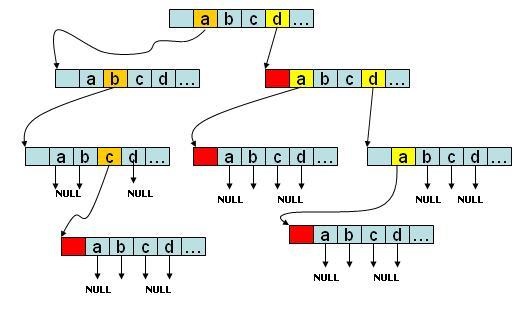
如上图，这种实现的特点是：每个节点都由指针数组存储，每个节点的所有子节点都位于一个数组之中，每个数组都是完全一样的。对于英文而言，每个数组有27个指针，其中一个作为词的终结符，另外 26 个依次代表字母表中的一个字母，对应指针指向下一个状态，若没有后续字符则指向NULL。

由于数组取词的复杂度为O(1)，因此这种实现的 Trie 树效率非常的高，比如要在一个节点中写入字符“c”，则直接在相应数组的第三个位置标入状态即可，而要确定字母“b”是否在现有节点的子节点之中，检查子节点所在数组第二个元素是否为空即可，这种实现巧妙的利用了等长数组中元素位置和值的一一对应关系，完美的实现了了寻址、存值、取值的统一。

但其缺点也很明显，它强制要求链路每一层都要有一个数组，每个数组都必须等长，这在实际应用中会造成大多数的数组指针空置（从上图就可以看出），事实上，对于真实的词典而言，公共前缀相对于节点数量而言还是太少，这导致绝大多数节点下并没有太多子节点。而对于中文这样具有大量单字的语言，若采取这样的实现，空置指针的数量简直不可想象。因此，经典 Trie 树是一种典型的以“空间换时间”的实现方式。一般只是拿来用于课程设计和新手练习，很少实际应用。

List Trie 树

由于数组的长度是不可变，因此经典 Trie 树存在着明显的空间浪费。但是如果将每一层都换成可变数组（不同语言对这种数据结构称呼不同，比如在 Python 中为List，C# 称为 LinkedList）来存储节点（见下图），每层可以根据节点的数量动态调整数组的长度，就可以避免大量的空间浪费。下图就是这种实现的图例：

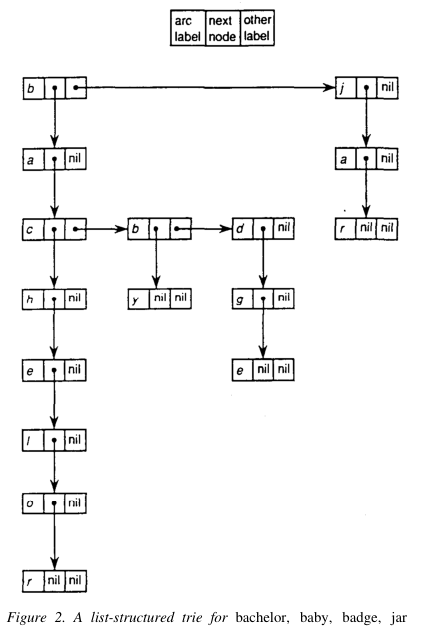
但是可变长数组的取词复杂度是O(d),其中 d 为数组的长度，这意味着状态转移函数无法通过映射转移到下一节点，必须先遍历数组，找到节点后再做转移，因此Trie 树实际时间复杂度变为O(m*n)(其中n为每层数组中节点的数量)。这显然降低了查询效率,因此还算不上完善。

Hash Trie 树

可变数组取词速度太慢，于是就有人想起用一组键值对（Java中可用HashMap类型，Python 中为 dict 类型，C#为Dictionary类型）代替可变数组：其中每个节点包含一组 Key-Value，每个 Key 对应该节点下的一个子节点字符，value 则指向相应的后一个状态。这种方式可以有效的减少空间浪费，同时由于键值对本质上就是一个哈希实现，因此理论上其查词效率也很高（理想状态下取词复杂度为O(1)）。但是哈希有的缺点，这种实现的 Trie 树也会有：

为了尽可能的避免键值冲突，哈希表需要额外的空间避开碰撞，因此仍有一部分的空间会被浪费；
哈希表很难做到完美，尤其是数据体量增大之后，其查词复杂度常常难以维持在O(1)，同时，对哈希值的计算也需要额外的时间，因此实际查询效率要比经典实现低，其具体复杂度由相应的哈希实现来定。

与数组和可变数组实现相比，这种实现做到了空间和时间上的一种平衡，这个结果并不意外，因为哈希表本身就是平衡数组（查寻迅速、增删悲剧）和可变数组（增删迅速，查询悲剧）相应优点和缺点的一种数据结构。总体而言，Hash Trie 结构简单，性能堪用，而且由于哈希实现可以为每个节点分配唯一的id,因此可以做到节点的实时动态添加（这点是非常大的优势）因此对于中小规模的词典或者对词典的实时更新有需求的应用，该实现非常适合。

Double-array Trie 树

双数组 Trie 树是目前 Trie 树各种实现中性能和存储空间均达到很好效果的实现。但其完整的实现比较复杂，对于新手而言入手相对较难。

Base Array 的作用

双数组 Trie 树和经典 Trie 树一样，也是用数组实现 Trie 树。只不过它是将所有节点的状态都记录到一个数组之中（Base Array），以此避免数组的大量空置。以行文开头的示例为例，每个字符在 Base Array 中的状态可以是这样子的：

好吧，我撒了个慌，事实上，为了能使单个数组承载更多的信息，Base Array 仅仅会通过数组的位置记录下字符的状态（节点），比如用数组中的位置 2 指代“清”节点、位置 7 指代 “中”节点；而数组中真正存储的值其实是一个整数，这个整数我们称之为“转移基数”，比如位置2的转移基数为 base[2]=3位置7的转移基数为base[7]=2，因此在不考虑叶子节点的情况下， Base Array 是这样子的：

转移基数是为了在一维数组中实现 Trie 树中字符的链路关系而设计的，举例而言，如果我们知道一个词中某个字符节点的转移基数，那么就可以据此推断出该词下一个节点在 Base Array 中的位置：比如知道 “清华”首字的转移基数为base[2]=3，那么“华”在数组中的位置就为base[2]+code("华")，这里的code("华")为字符表中“华”的编码，假设例树的字符编码表为：

清-1，华-2，大-3，学-4，新-5，中-6，人-7

那么“华”的位置应该在Base Array 中的的第 5 位（base[2]+code("华")=3+2=5）：

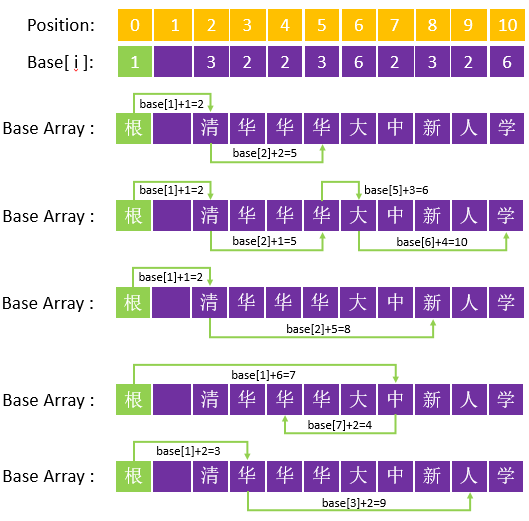
而所有词的首字，则是通过根节点的转移基数推算而来。因此，对于字典中已有的词，只要我们每次从根节点出发，根据词典中各个字符的编码值，结合每个节点的转移基数，通过简单的加法，就可以在Base Array 中实现词的链路关系。以下是“清华”、“清华大学”、“清新”、“中华”、“华人”五个词在 Base Array 中的链路关系：

Reference

Wikipedia Trie - https://zh.wikipedia.org/wiki/Trie
6天通吃树结构—— 第五天 Trie树 - https://www.cnblogs.com/huangxincheng/archive/2012/11/25/2788268.html
Trie树（Prefix Tree）介绍 - https://blog.csdn.net/lisonglisonglisong/article/details/45584721
Trie树（字典树） - https://wizardforcel.gitbooks.io/the-art-of-programming-by-july/content/06.09.html
小白详解 Trie 树 - https://segmentfault.com/a/1190000008877595

【Data Structure】Tries树（字典树）