栈的应用
栈是一种很重要的数据结构,在计算机中有着很广泛的应用,如下一些操作都应用到了栈。
- 符号匹配,HTML和XML文件中的标签匹配
- 中缀表达式(Infix Expressions)转换为后缀表达式(Postfix Expressions)
- 实现函数的嵌套调用
- 表达式求值
- 网页浏览器中已访问页面的历史记录
符号匹配
在编写程序的过程中,我们经常会遇到诸如圆括号“()”与花括号“{}”,这些符号都必须是左右匹配的,这就是我们所说的符合匹配类型,当然符合不仅需要个数相等,而且需要先左后右的依次出现,否则就不符合匹配规则,如“)(”,明显是错误的匹配,而“()”才是正确的匹配。有时候符合如括号还会嵌套出现,如“9-(5+(5+1))”,而嵌套的匹配原则是一个右括号与其前面最近的一个括号匹配。
事实上编译器帮我们检查语法错误时,也是执行一样的匹配原理,而这一系列操作都需要借助栈来完成,接下来我们使用栈来实现括号”()”是否匹配的检测。
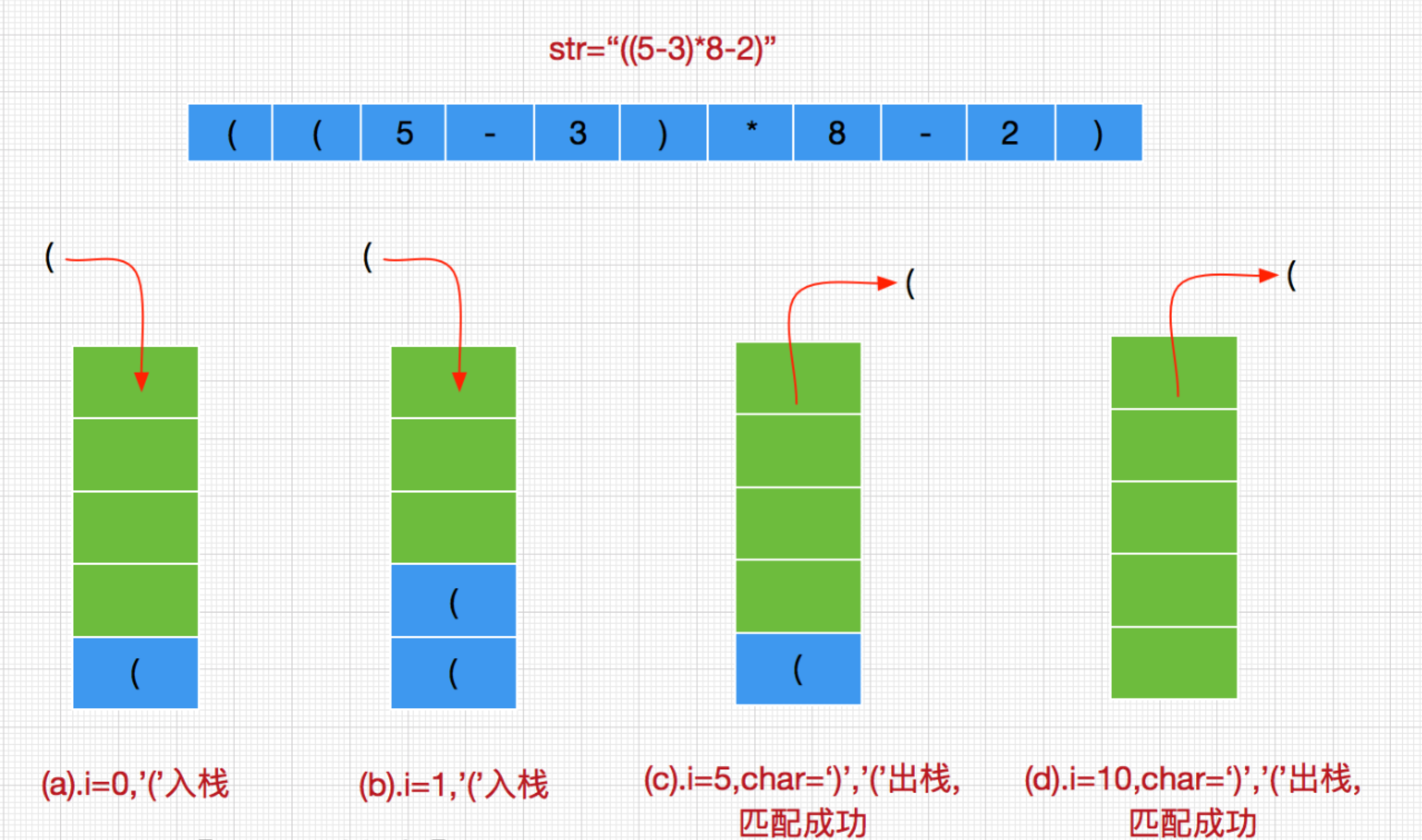
以str=”((5-3)*8-2)”为例。
a. str是一个表达式字符串,从左到右依次对字符串str中的每个字符char进行语法检测,如果char是左括号,则入栈,如果char是右括号,则出栈(有一对匹配就可以去匹配一个左括号,因此可以出栈),若此时出栈的字符char为左括号,则说明这一对括号匹配正常。如果此时栈为空或者出栈字符不为左括号,则表示缺少与char匹配的左括号,即目前不完整。
b. 重复执行a操作,直到str检测结束,如果此时栈为空,则全部括号匹配,如果栈中还有左括号,是说明缺少右括号。
中缀表达式(Infix Expressions)转换为后缀表达式(Postfix Expressions)
中缀表达式(Infix Expressions)
我们先来了解一下什么是中缀表达式(Infix Expressions),数学里面的公式都是中缀表达式,如以下的表达式:
1+3*(9-2)+9
定义:将运算符写在两个操作数中间的表达式称为中缀表达式。
在中缀表达式中,运算符拥有不同的优先级,同时也可以使用圆括号改变运算次序,由于这两点的存在,使用的中缀表达式的运算规则比较复杂,求值的过程不能从左往右依次计算,当然这也是相对计算机而言罢了,毕竟我们日常生活的计算使用的还是中缀表达式。
既然计算机感觉复杂,那么我们就需要把中缀表达式转化成计算机容易计算而且不复杂的表达式,这就是后缀表达式了。
前缀表达式和后缀表达式
波兰数学家Jan Lukasiewicz提出了另一种数学表示法,它有两种表示形式:
- 把运算符写在操作数之前,称为波兰表达式(Polish Expression)或前缀表达式(Prefix Expression),如+AB;
- 把运算符写在操作数之后,称为逆波兰表达式(Reverse Polish Expression)或后缀表达式(Suffix Expression),如AB+;
后缀表达式(Postfix Expressions)/逆波兰表达式(Reverse Polish Expression)
后缀表达式(Postfix Expressions),也称为逆波兰表达式(Reverse Polish Expression)。
在后缀表达式中,运算符(Operator)放在两个操作数(Operand)的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不用考虑运算符的优先级)。
如下我们将中缀表达式转为后缀表达式:
//1+3*(9-2)+9 转化前的中缀表达式
//1 3 9 2 - * + 9 + 转化后的后缀表达式
// 2 * (9 + 6 / 3 - 5) + 4 转化前的中缀表达式
// 2 9 6 3 / + 5 - * 4 + 转化后的后缀表达式
中缀转后缀的转换过程需要用到一个栈和一个数组,这个栈用于协助转换,数组用于存放转化后的后缀表达式。
具体过程如下:
- 如果:
- 遇到操作数,就直接将其放入数组中;
- 遇到左括号,就直接进栈。
- 遇到右括号,则将栈元素(运算符)不断弹出,并将弹出的运算符依次存入数组中,若遇到左括号后弹出停止。注意,左括号只弹出栈但不存入数组。
- 遇到运算符
+,-,*或\,则将其放入到栈中:- 若该运算符优先级大于栈顶运算符, 则把它压入栈;
- 若该运算符优先级小于等于栈顶运算符,将栈顶运算符出栈,并将其放入数组中;再比较新的栈顶运算符, 直到该运算符大于栈顶运算符优先级为止,然后将该运算符压入栈;
- 读到了输入的末尾,则将栈中所有元素依次弹出存入到数组中。
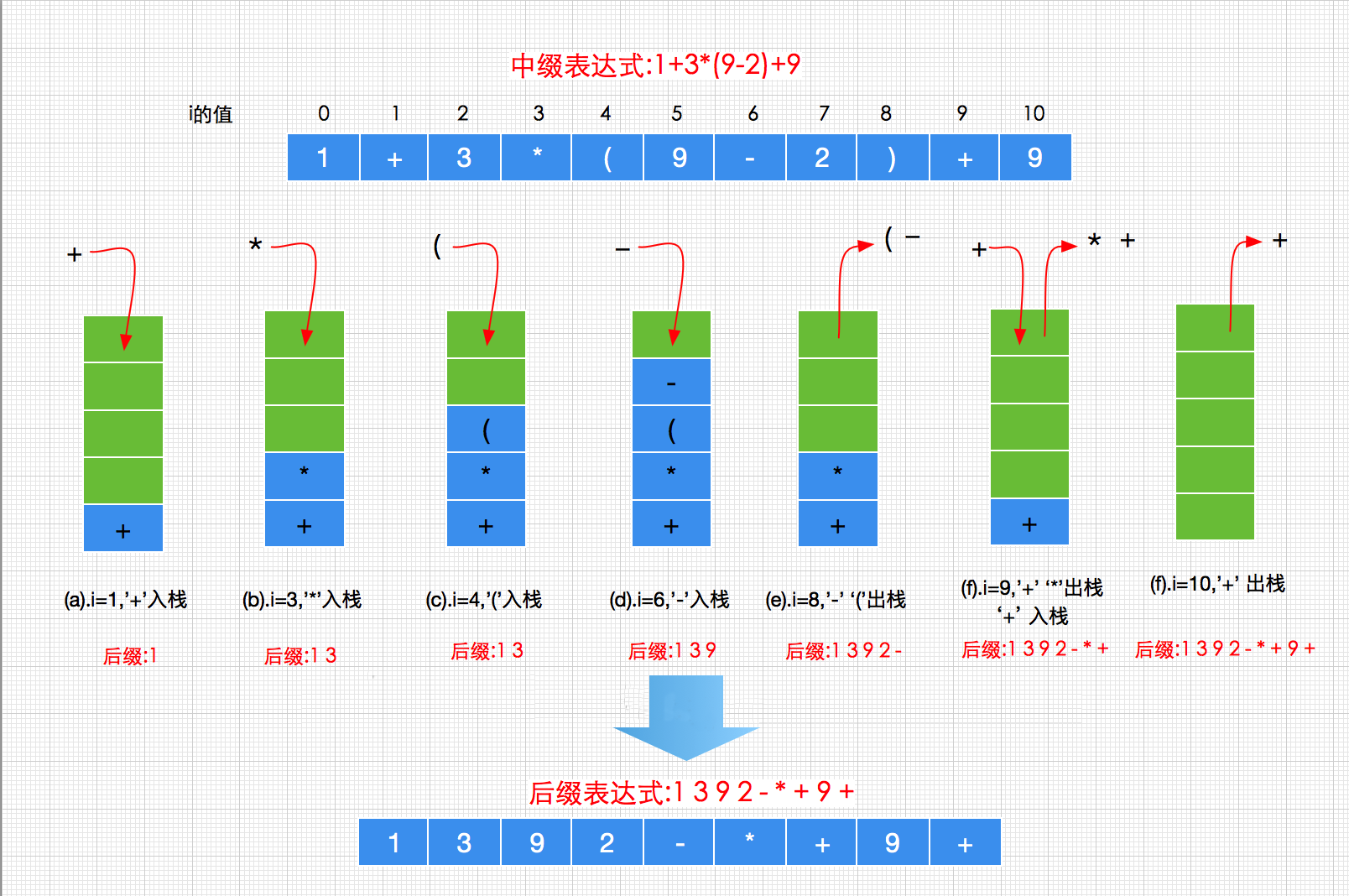
到此中缀表达式转化为后缀表达式完成,数组存储的元素顺序就代表转化后的后缀表达式。
执行图示过程如下:
求值的简化方法
比如,要将中缀表达式(a+b)c(d-e/f) 转成后缀表达式。
- 首先按照运算的先后顺序将表达式全部都添加上括号;
(a+b)c(d-e/f)--->> (((a+b)c)((d-(e/f)))) - 然后由于是后缀表达式,从里到外将所有运算符都拿到右括号的右边;
(((ab)+c)((d(ef)/)-)) - 最后再将所有括号都去掉。
ab+c*def/-*
同理,如果是变为前缀表达式的话,就把运算符拿到括号左边。
中缀表达式(Infix Expressions)转换为后缀表达式(Postfix Expressions)的实现
/**
* 中缀转后缀
* @param expstr 中缀表达式字符串
* @return
*/
public static String toPostfix(String expstr)
{
//创建栈,用于存储运算符
SeqStack<String> stack = new SeqStack<>(expstr.length());
String postfix="";//存储后缀表达式的字符串
int i=0;
while (i<expstr.length())
{
char ch=expstr.charAt(i);
switch (ch)
{
case '+':
case '-':
//当栈不为空或者栈顶元素不是左括号时,直接出栈,因此此时只有可能是*/+-四种运算符(根据规则4),否则入栈
while (!stack.isEmpty() && !stack.peek().equals("(")) {
postfix += stack.pop();
}
//入栈
stack.push(ch+"");
i++;
break;
case '*':
case '/':
//遇到运算符*/
while (!stack.isEmpty() && (stack.peek().equals("*") || stack.peek().equals("/"))) {
postfix += stack.pop();
}
stack.push(ch+"");
i++;
break;
case '(':
//左括号直接入栈
stack.push(ch+"");
i++;
break;
case ')':
//遇到右括号(规则3)
String out = stack.pop();
while (out!=null && !out.equals("("))
{
postfix += out;
out = stack.pop();
}
i++;
break;
default:
//操作数直接入栈
while (ch>='0' && ch<='9')
{
postfix += ch;
i++;
if (i<expstr.length())
ch=expstr.charAt(i);
else
ch='=';
}
//分隔符
postfix += " ";
break;
}
}
//最后把所有运算符出栈(规则5)
while (!stack.isEmpty())
postfix += stack.pop();
return postfix;
}
计算后缀表达式
转成后缀后,我们来看看计算机如何利用后缀表达式进行结果运算,通过前面的分析可知,后缀表达式是没有括号的,而且计算过程是按照从左到右依次进行的,因此在后缀表达的求值过程中,当遇到运算符时,只需要取前两个操作数直接进行计算即可,而当遇到操作数时不能立即进行求值计算,此时必须先把操作数保存等待获取到运算符时再进行计算,如果存在多个操作数,其运算次序是后出现的操作数先进行运算,也就是后进先运算,因此后缀表达式的计算过程我们也需要借助栈来完成,该栈用于存放操作数,后缀表达式的计算过程及其图解如下:
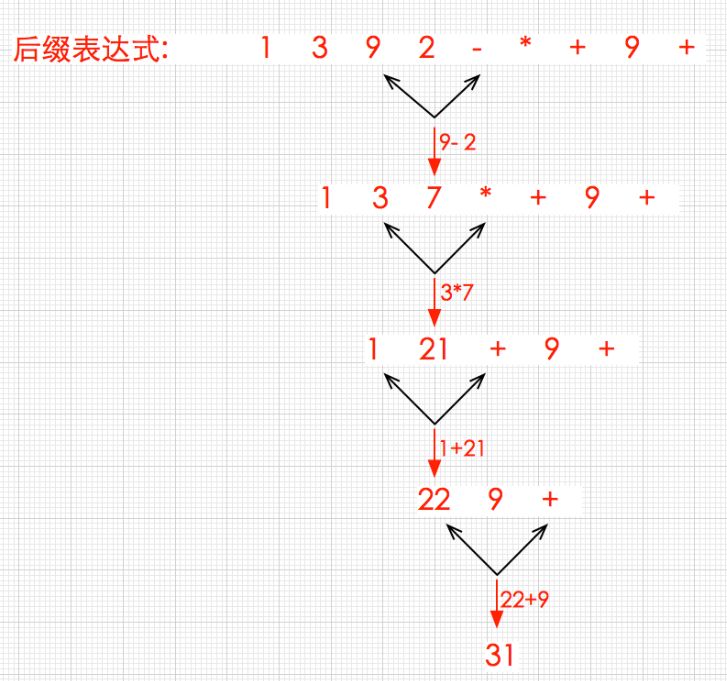
借助栈的程序计算过程:
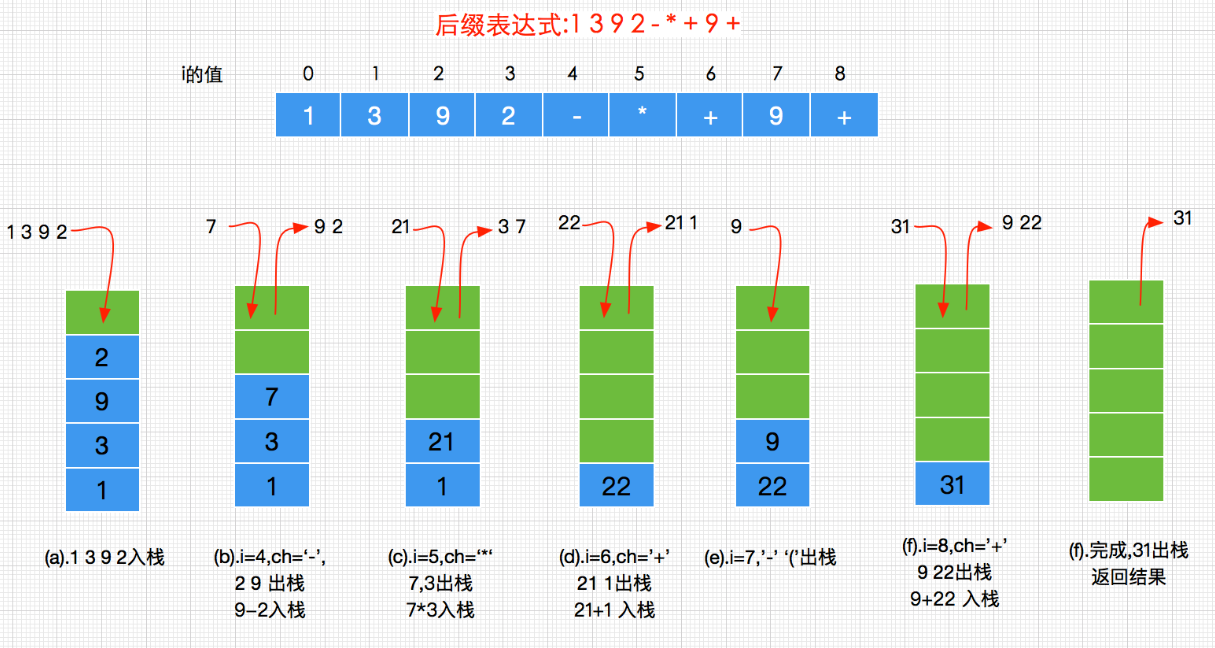
简单分析说明一下:
- 如果ch是数字,先将其转换为整数再入栈;
- 如果是运算符,将两个操作数出栈,计算结果再入栈;
- 重复1)和2)直到后缀表达式结束,最终栈内的元素即为计算的结果。
计算后缀表达式的值的实现
public class CalculateExpression {
/**
* 计算后缀表达式的值
* @param postfix 传入后缀表达式
* @return
*/
public static int calculatePostfixValue(String postfix)
{
//栈用于存储操作数,协助运算
LinkedStack<Integer> stack = new LinkedStack<>();
int i=0, result=0;
while (i<postfix.length())
{
char ch=postfix.charAt(i);
if (ch>='0' && ch<='9')
{
result=0;
while (ch!=' ')
{
//将整数字符转为整数值ch=90
result = result*10 + Integer.parseInt(ch+"");
i++;
ch = postfix.charAt(i);
}
i++;
stack.push(result);//操作数入栈
}
else
{ //ch 是运算符,出栈栈顶的前两个元素
int y= stack.pop();
int x= stack.pop();
switch (ch)
{ //根据情况进行计算
case '+': result=x+y; break;
case '-': result=x-y; break;
case '*': result=x*y; break;
case '/': result=x/y; break; //注意这里并没去判断除数是否为0的情况
}
//将运算结果入栈
stack.push(result);
i++;
}
}
//将最后的结果出栈并返回
return stack.pop();
}
//测试
public static void main(String args[])
{
String expstr="1+3*(9-2)+90";
String postfix = toPostfix(expstr);
System.out.println("中缀表达式->expstr= "+expstr);
System.out.println("后缀表达式->postfix= "+postfix);
System.out.println("计算结果->value= "+calculatePostfixValue(postfix));
}
}
实现函数的嵌套调用
操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构,用来存储函数调用时的临时变量。
每进入一个函数,就会将函数中是所有的临时变量存入一个栈帧,并将这个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈。
示例:
int main() {
int a = 1;
int ret = 0;
int res = 0;
ret = add(3, 5);
res = a + ret;
printf("%d", res);
reuturn 0;
}
int add(int x, int y) {
int sum = 0;
sum = x + y;
return sum;
}
在main() 函数中调用了 add() 函数,获取计算结果,并且与临时变量 a 相加,最后打印 res 的值。这个过程的中函数栈里的出栈、入栈操作,如下所示:
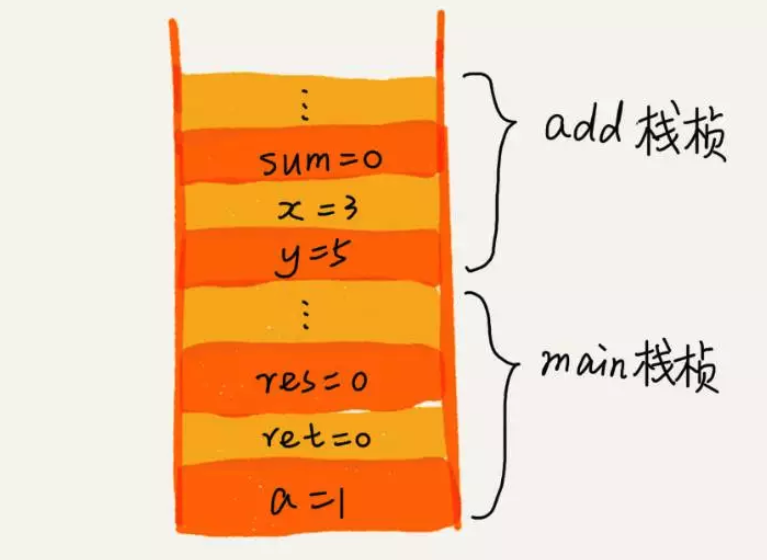
思考:为什么函数要用栈来保存临时变量呢?用其他数据结构不行吗?
函数调用的局部状态之所以用栈来记录是因为这些状态数据的存活时间满足“后入先出”(LIFO)顺序,而栈的基本操作正好就是支持这种顺序的访问。
栈是程序设计中的一种经典数据结构,每个程序都拥有自己的程序栈。栈帧也叫过程活动记录,是编译器用来实现函数调用过程的一种数据结构。C语言中,每个栈帧对应着一个未运行完的函数。从逻辑上讲,栈帧就是一个函数执行的环境:函数调用框架、函数参数、函数的局部变量、函数执行完后返回到哪里等等。栈是从高地址向低地址延伸的。每个函数的每次调用,都有它自己独立的一个栈帧,这个栈帧中维持着所需要的各种信息。
寄存器ebp(base pointer)指向当前的栈帧的底部(高地址),可称为“帧指针”或“基址指针”;寄存器esp(stack pointer)指向当前的栈帧的顶部(低地址),可称为“ 栈指针”。
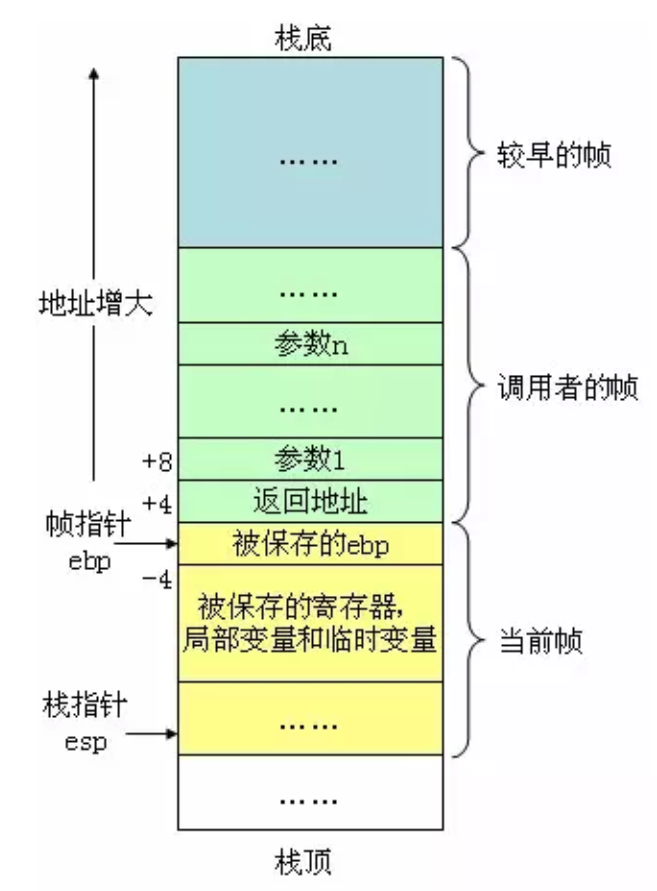
在C和C++语言中,临时变量分配在栈中,临时变量拥有函数级的生命周期,即“在当前函数中有效,在函数外无效”。这种现象就是函数调用过程中的参数压栈,堆栈平衡所带来的。堆栈平衡是指函数调完成后,要返还所有使用过的栈空间。
函数调用其实可以看做4个过程:
- 压栈: 函数参数压栈,返回地址压栈
- 跳转: 跳转到函数所在代码处执行
- 执行: 执行函数代码
- 返回: 平衡堆栈,找出之前的返回地址,跳转回之前的调用点之后,完成函数调用
表达式求值
以 3 + 5 x 8 - 6 为这个表达式为例,编译器是如何利用栈来实现表达式求值的呢?
编译器会使用两个栈来实现,一个栈用来保存操作数(称为操作数栈),另一个栈用来保存运算符(称为运算符栈)。
从左向右遍历表达式:
- 当遇到数字就直接压入操作数栈;
- 当遇到操作符,要看看当前操作数栈中是否有元素
- 如果没有元素,就将这个操作符直接压入运算符栈;
- 如果有元素,就要将当前操作符与运算符栈的栈顶元素进行比较:
- 如果比运算符栈顶元素的优先级高,就将当前运算符压入运算符栈;
- 如果比运算符栈顶元素的优先级低或者相同,先从运算符栈中取栈顶运算符,再从操作数栈的栈顶依次取 2 个操作数,然后进行计算。计算完成后,把计算的结果压入操作数栈。继续比较。
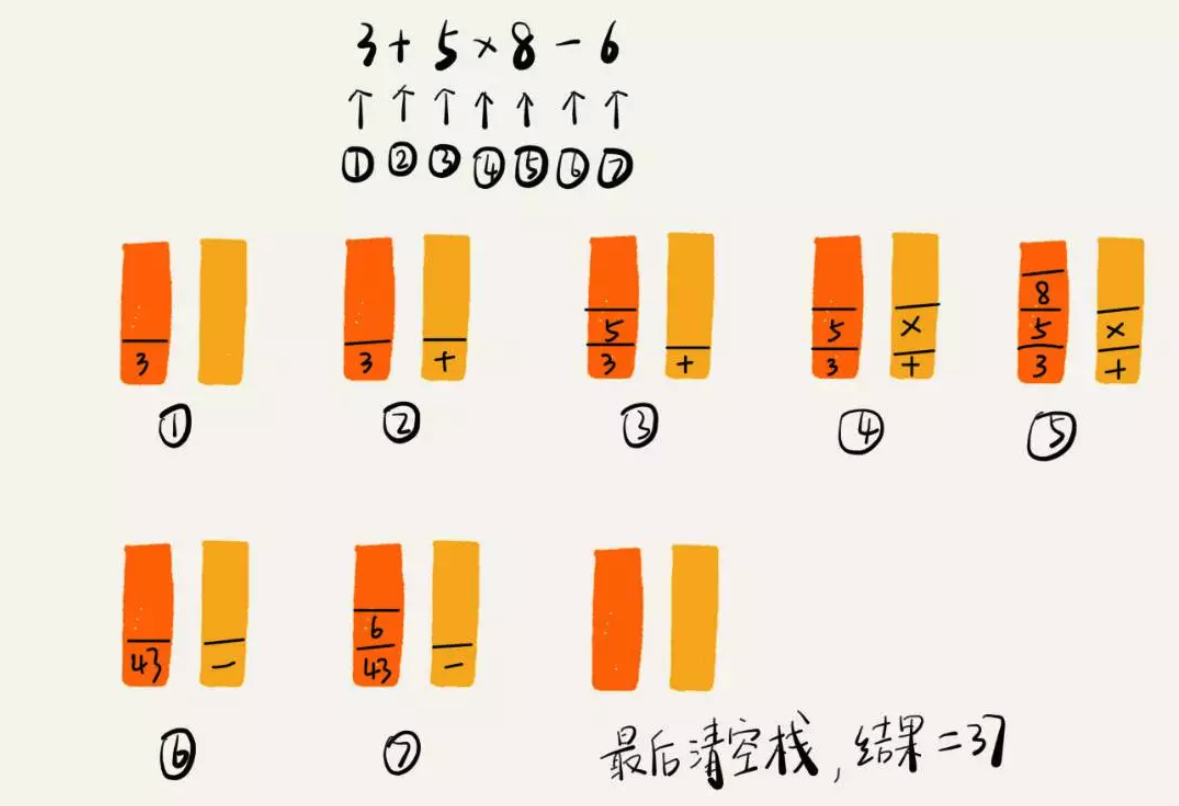
网页浏览器中已访问页面的历史记录
使用两个栈,X 和 Y,把首次浏览的页面依次压入栈 X,当点击后退按钮时,再依次从栈 X 中出栈,并将出栈的数据依次放入栈 Y。当我们点击前进按钮时,我们依次从栈 Y 中取出数据,放入栈 X 中。当栈 X 中没有数据时,那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
比如你顺序查看了 a,b,c 三个页面,我们就依次把 a,b,c 压入栈,这个时候,两个栈的数据就是这个样子:
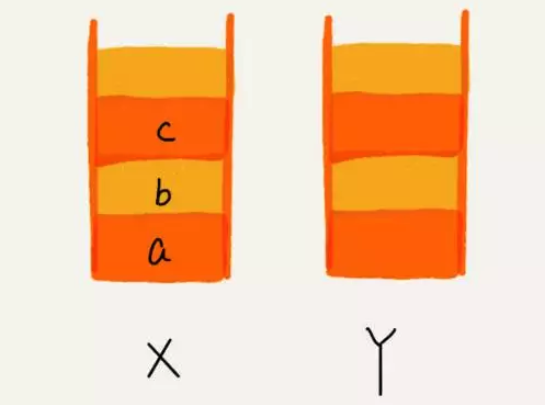
当你通过浏览器的后退按钮,从页面 c 后退到页面 a 之后,我们就依次把 c 和 b 从栈 X 中弹出,并且依次放入到栈 Y。这个时候,两个栈的数据就是这个样子:
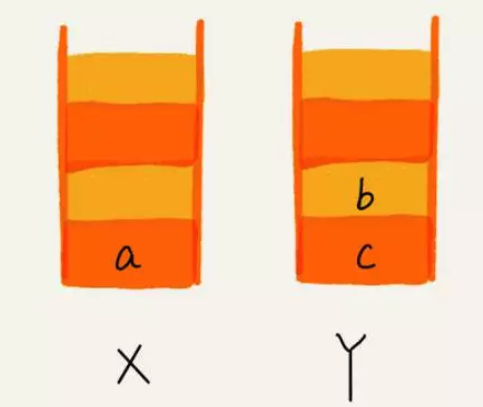
这个时候你又想看页面 b,于是你又点击前进按钮回到 b 页面,我们就把 b 再从栈 Y 中出栈,放入栈 X 中。此时两个栈的数据是这个样子:
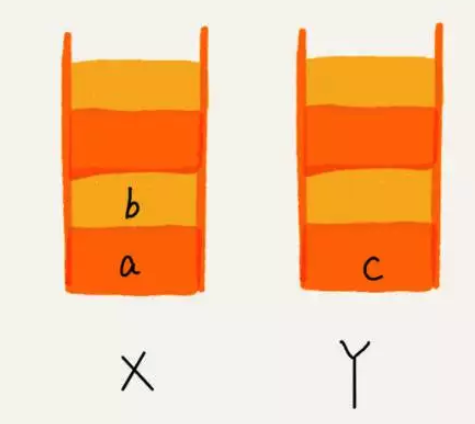
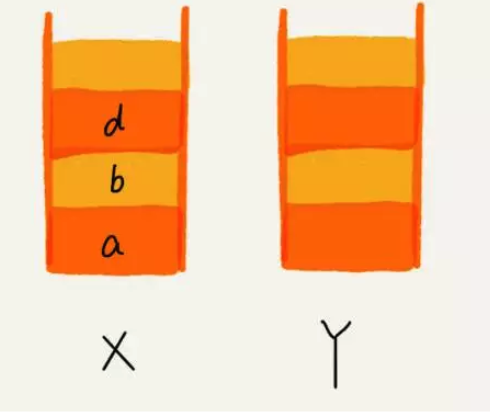
这个时候,你通过页面 b 又跳转到新的页面 d 了,页面 c 就无法再通过前进、后退按钮重复查看了,所以需要清空栈 Y。此时两个栈的数据这个样子:
Reference
- 数据结构与算法 | 栈的实现及应用 - https://juejin.im/post/5c3be7d5e51d455230711a27#heading-17