Bitmap
所谓的 Bit-map 就是用一个 bit 位来标记某个元素对应的 Value, 而 Key 即是该元素。由于采用了 Bit 为单位来存储数据,因此在存储空间方面,可以大大节省。
实现
举个例子,假如有10亿个int数,10亿个 int 数大约是占用 $10 * 10^8 * 4 Byte = 4 GB$(注意,在 Java 中,一个 int 占用 4 个字节)。
如果对这样大的一个数据集做查找和排序,对内存的消耗是相当大的,有人说,这些数据可以不用一次性加载,那就是要存盘了,存盘必然消耗I/O,则意味着处理速度的变慢。
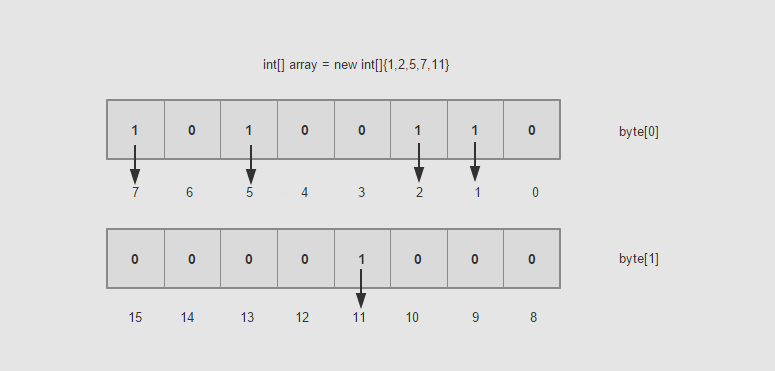
如果用BitMap思想来解决的话,就好很多。一个byte是占8个bit,如果每一个bit的值就是有或者没有,也就是二进制的0或者1,如果用bit的位置代表数组值有还是没有,那么0代表该数值没有出现过,1代表该数组值出现过。对应占用的内存为 $2^{32} bit = 2^{32}/8 Byte = 2^{29} Byte = 512 MB$ 。具体如下图:
bitmap算法代码实现
class BitMap {
private long maxValue;
private static int[] words;
//构造函数中传入数据中的最大值(范围为 1-最大值)
public BitMap(long maxValue) {
this.maxValue = maxValue;
// 根据长度算出,所需数组大小
words = new int[(int) ((maxValue - 1) >> 5)]; // 用移位运算代替除法,效率更高
}
public int getBit(long index) {
int word = words[(int) ((index - 1) >> 5)];
// (index - 1) & 31 相当于对 index-1 按 32 求余数
int offset = (int) ((index - 1) & 31);
return (word >> offset) & 0x01;
}
public void setBit(long index) {
// 求出该index - 1所在bitMap的下标
int wordIndex = (int) ((index - 1) >> 5);
// 求出该值的偏移量(求余)
int offset = (int) ((index - 1) & 31);
int word = words[wordIndex];
words[wordIndex] = word | (0x01 << offset);
(words[wordIndex] & (bitIndex >> 1L))
}
public static void main(String[] args) {
BitMap bitMap = new BitMap(32);
bitMap.setBit(32);
System.out.println(bitMap.getBit(1));
System.out.println(bitMap.getBit(32));
}
}
问题实例
问题1
在 2.5 亿个整数中找出不重复的整数,注,内存不足以容纳这 2.5 亿个整数。
解法
解法一:采用 2-Bitmap(每个数分配 2bit,00 表示不存在,01 表示出现一次,10 表示多次, 11 无意义)进行,共需内存 $2^{32} * 2 bit=1 GB$ 内存,还可以接受。然后扫描这 2.5 亿个整数, 查看 Bitmap 中相对应位,如果是 00 变 01,01 变 10,10 保持不变。所描完事后,查看 bitmap, 把对应位是 01 的整数输出即可。
举个例子,例如我们此时读入一个数是:64,64对应的所在bit位是:64*2=128,也就是说第 127 和 128 位共同标示了它的出现状态(公式为:2 *(x - 1) -1 和 2 *(x - 1) 位)。其他的以此类推。每当我们读出一个数,我们就这样去找到它对应的bit位,先读出bit位的值,再做记录,已经是01的,再次来到,那么就应该修改为10。最后的我们这样得出结果:扫描整个位图,如果是10的,就下标/2得出这个数。
或者,进行划分小文件的方法。然后在小文件中找出不重复的整数,并排序。然后再进行归并,注意去除重复的元素。”
问题2
给 40 亿个不重复的 unsigned int 的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那 40 亿个数当中?
解法
可以用位图(Bitmap) 的方法,申请 512M 的内存,一个 bit 位代表一个 unsigned int 值。 读入 40 亿个数,设置相应的 bit 位,读入要查询的数,查看相应 bit 位是否为 1,为 1 表示存在, 为 0 表示不存在。
Reference
- 《编程之法:面试和算法心得》