栈（Stack）

栈（Stack），是一种有序特殊的线性表，只允许在有序的线性数据集合的一端（称为堆栈顶端，top）进行加入（push）数据和移除（pop）数据的运算。因而按照**后进先出（LIFO, Last In First Out）**的原理运作。

栈的基本操作创建栈，判空，入栈，出栈，获取栈顶元素等，注意栈不支持对指定位置进行删除，插入。

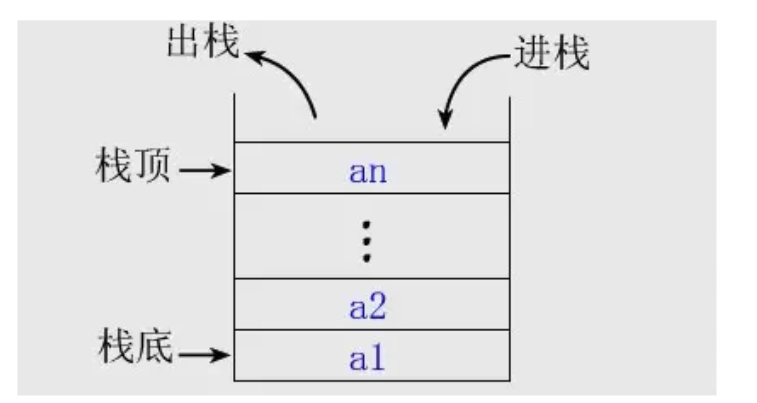
其实非常好理解，我们将栈可以看成一个箱子：

往箱子里面放东西叫做入栈（push）；
往箱子里面取东西叫做出栈（pop）；
箱子的底部叫做栈底（bottom）；
箱子的顶部叫做栈顶（top）。

说到栈的特性，肯定会有一句经典的言语来概括：先进后出（LIFO, Last In First Out）。

Stack这种数据结构用途很广泛，在计算机的使用中，大量的运用了栈，比如编译器中的词法分析器、Java虚拟机、软件中的撤销操作（Undo）、浏览器中的回退操作，编译器中的函数调用实现等等。

栈接口抽象数据类型

public interface Stack<T> {
   /**
    * 栈是否为空
    * @return
    */
   boolean isEmpty();

   /**
    * data元素入栈
    * @param data
    */
   void push(T data);

   /**
    * 返回栈顶元素,未出栈
    * @return
    */
   T peek();

   /**
    * 出栈,返回栈顶元素,同时从栈中移除该元素
    * @return
    */
   T pop();
}

栈的实现

栈可以有两种实现：

静态栈（数组实现）- 顺序栈（Sequence Stack）
动态栈（链表实现）- 链式栈（Linked Stack）

顺序栈（Sequence Stack）的设计

顺序栈，顾名思义就是采用顺序表实现的的栈，

public class SeqStack<T> implements Stack<T>,Serializable {

    private static final long serialVersionUID = -5413303117698554397L;

    /**
     * 栈顶指针,-1代表空栈
     */
    private int top=-1;

    /**
     * 容量大小默认为10
     */
    private int capacity=10;

    /**
     * 存放元素的数组
     */
    private T[] array;

    private int size;

    public SeqStack(int capacity){
        array = (T[]) new Object[capacity];
    }

    public SeqStack(){
        array= (T[]) new Object[this.capacity];
    }
    //.......省略其他代码
}

peek()

获取栈顶元素值的peek操作过程如下图（未删除只获取值）：

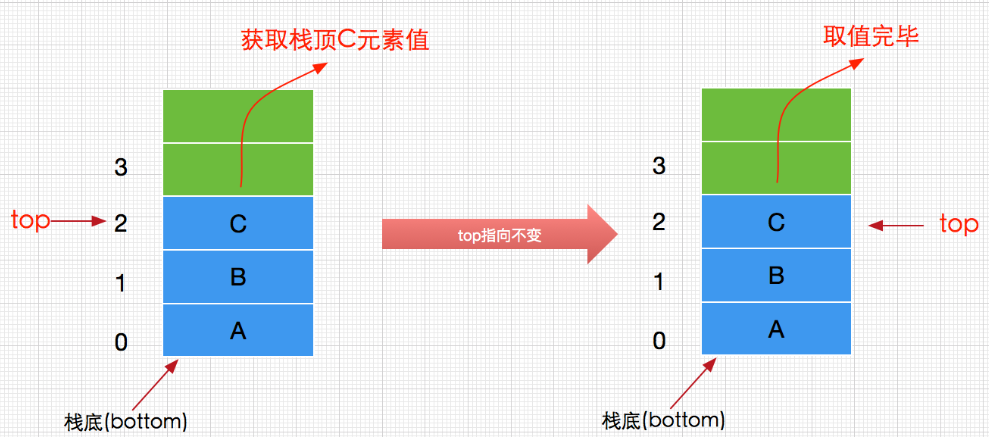
实现

/**
  * 获取栈顶元素的值,不删除
  * @return
  */
 @Override
 public T peek() {
     if(isEmpty())
         new EmptyStackException();
     return array[top];
 }

push()

从栈添加元素的过程如下（更新栈顶top指向）：

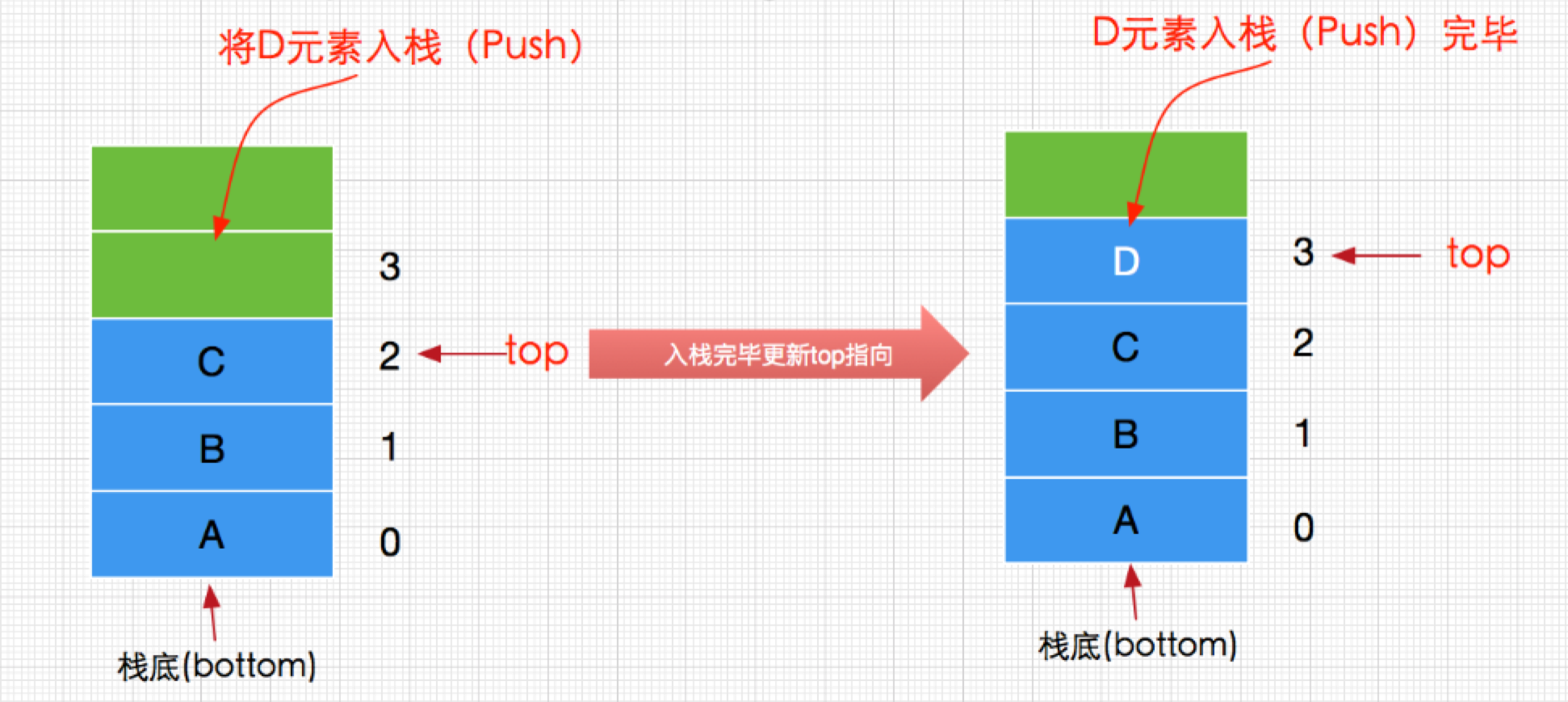
实现

/**
 * 添加元素,从栈顶(数组尾部)插入
 * 容量不足时，需要扩容
 * @param data
 */
@Override
public void push(T data) {
    //判断容量是否充足
    if(array.length==size)
        ensureCapacity(size*2+1);//扩容

    //从栈顶添加元素
    array[++top]=data;
}

pop()

栈弹出栈顶元素的过程如下（删除并获取值）：

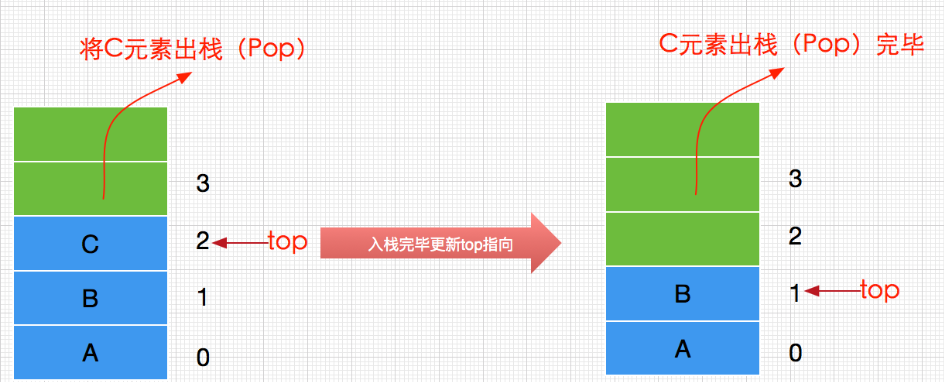
实现

/**
  * 从栈顶(顺序表尾部)删除
  * @return
  */
 @Override
 public T pop() {
     if(isEmpty())
         new EmptyStackException();
     size--;
     return array[top--];
 }

链式栈（Linked Stack）的设计

了解完顺序栈，我们接着来看看链式栈，所谓的链式栈（Linked Stack），就是采用链式存储结构的栈，由于我们操作的是栈顶一端，因此这里采用单链表（不带头结点）作为基础，直接实现栈的添加，获取，删除等主要操作即可。其操作过程如下图：

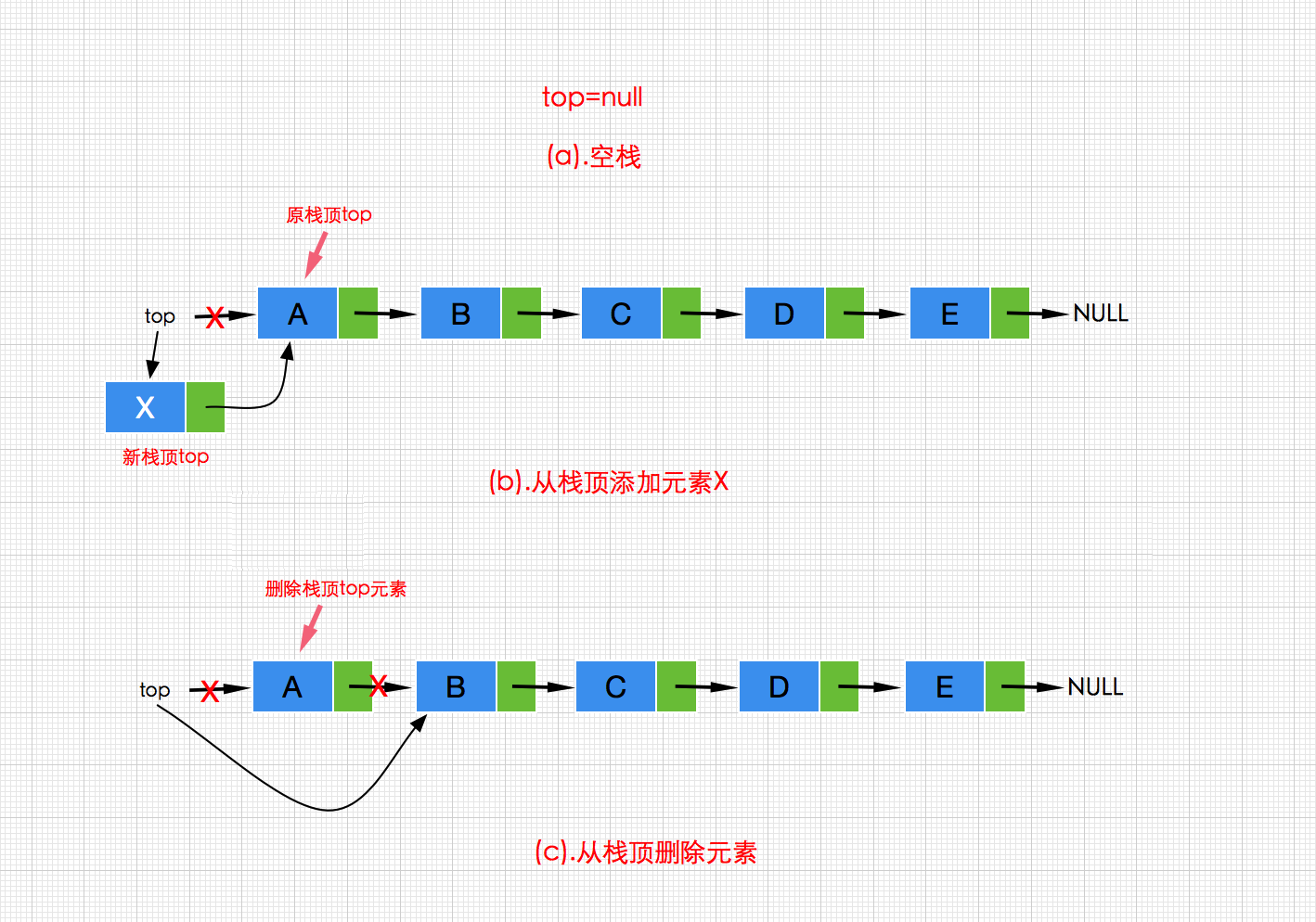
从图可以看出，无论是插入还是删除直接操作的是链表头部也就是栈顶元素，因此我们只需要使用不带头结点的单链表即可。代码实现如下

public class LinkedStack<T> implements Stack<T> ,Serializable{

    private static final long serialVersionUID = 1911829302658328353L;

    private Node<T> top;

    private int size;

    public LinkedStack(){
        this.top=new Node<>();
    }

    public int size(){
        return size;
    }


    @Override
    public boolean isEmpty() {
        return top==null || top.data==null;
    }

    @Override
    public void push(T data) {
        if (data==null){
            throw new StackException("data can\'t be null");
        }
        if(this.top==null){//调用pop()后top可能为null
            this.top=new Node<>(data);
        }else if(this.top.data==null){
            this.top.data=data;
        }else {
           Node<T> p=new Node<>(data,this.top);
            top=p;//更新栈顶
        }
        size++;
    }

    @Override
    public T peek()  {
        if(isEmpty()){
            throw new EmptyStackException("Stack empty");
        }

        return top.data;
    }

    @Override
    public T pop() {
        if(isEmpty()){
            throw new EmptyStackException("Stack empty");
        }

        T data=top.data;
        top=top.next;
        size--;
        return data;
    }
    //测试
    public static void main(String[] args){
        LinkedStack<String> sl=new LinkedStack<>();
        sl.push("A");
        sl.push("B");
        sl.push("C");
        int length=sl.size();
        for (int i = 0; i < length; i++) {
            System.out.println("sl.pop->"+sl.pop());
        }
    }
}

算法复杂度分析

我们来看看顺序栈与链式栈中各个操作的算法复杂度（时间和空间）对比。

顺序栈复杂度如下：

操作	时间复杂度
SeqStack空间复杂度(用于N次push)	O(n)
push()时间复杂度	O(1)*
pop()时间复杂度	O(1)
peek()时间复杂度	O(1)
isEmpty()时间复杂度	O(1)

注明：push操作在特定情况下会触发resize（此时时间复杂度为 O(N)），但平均时间复杂度是O(1)的。

链式栈复杂度如下：

操作	时间复杂度
SeqStack空间复杂度(用于N次push)	O(1)
push()时间复杂度	O(1)
pop()时间复杂度	O(1)
peek()时间复杂度	O(1)
isEmpty()时间复杂度	O(1)

Reference

java数据结构与算法之栈（Stack）设计与实现 - https://blog.csdn.net/javazejian/article/details/53362993
数据结构与算法 | 栈的实现及应用 - https://juejin.im/post/5c3be7d5e51d455230711a27#heading-17

【Data Structure】栈（Stack）