HashMap 类
HashMap类实现了 Map<K,V>接口,同时继承了抽象类 AbstractMap<E>。
HashMap是基于哈希表实现的,每一个元素是一个key-value对,其内部通过单链表解决冲突问题,容量不足(超过了阀值)时,同样会自动增长。
特点
- 非线程安全
- HashMap是非线程安全的,只适用于单线程环境下。而在多线程环境下,可以采用concurrent并发包下的concurrentHashMap。
- null值
- HashMap允许键或值为null。
- 但由于HashMap不允许重复的键(key),因此只有一条记录的键(key)可以是空值(null)。
- 当调用HashMap的get()方法返回null值时,既可以表示 HashMap中没有该键,也可以表示该键所对应的值为null。
- 因此,在HashMap中不能由get()方法来判断HashMap中是否存在某个键, 而应该用containsKey()方法来判断。
操作
添加元素
public Object put(Object Key,Object value)
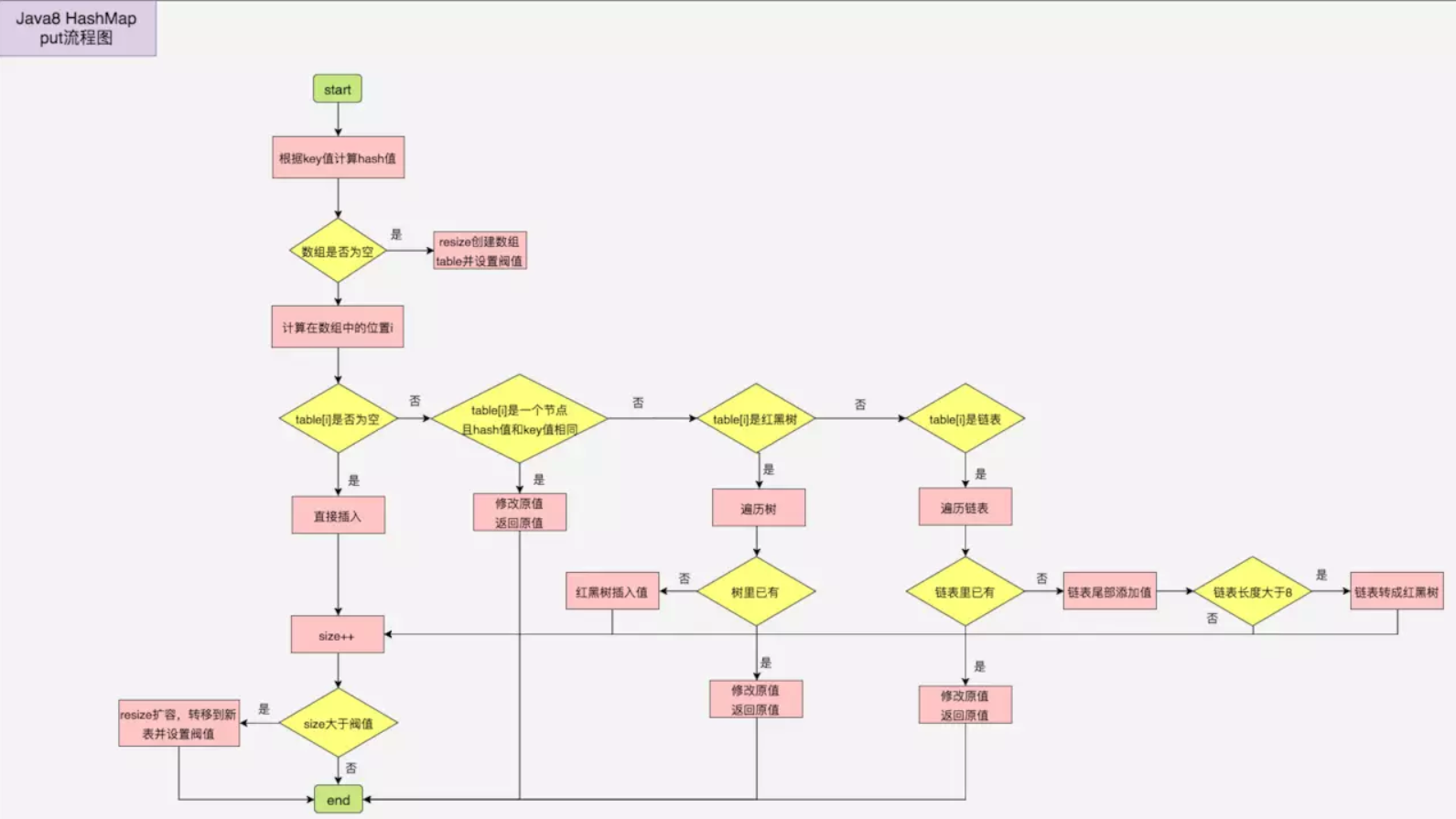
调用Put方法的时候发生了什么呢?
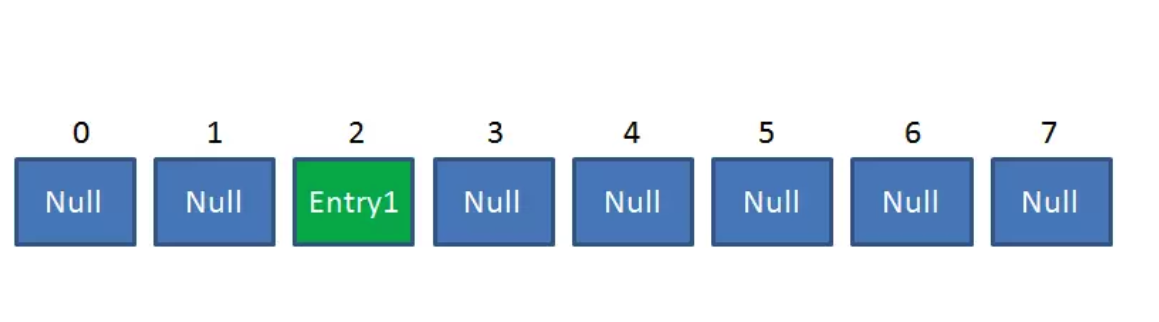
比如调用 hashMap.put(“apple”, 0) ,插入一个Key为“apple"的元素。这时候我们需要利用一个哈希函数来确定Entry的插入位置(index):
index = Hash(“apple”);
假定最后计算出的index是2,那么结果如下:
但是,因为HashMap的长度是有限的,当插入的Entry越来越多时,再完美的Hash函数也难免会出现哈希冲突(hash collision)的情况。比如下面这样:
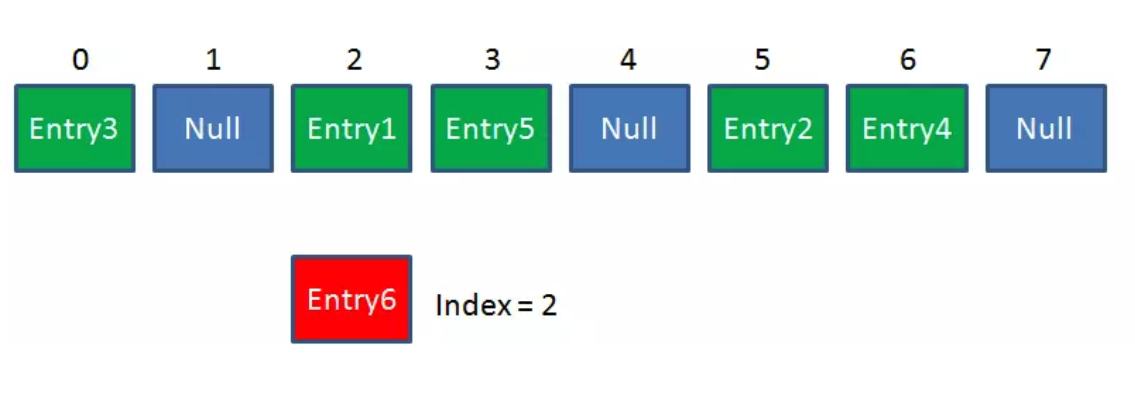
这时候该怎么办呢?我们可以利用链表来解决。
HashMap数组的每一个元素不止是一个Entry对象,也是一个链表的头节点。每一个Entry对象通过Next指针指向它的下一个Entry节点。当新来的Entry映射到冲突的数组位置时,只需要插入到对应的链表即可:
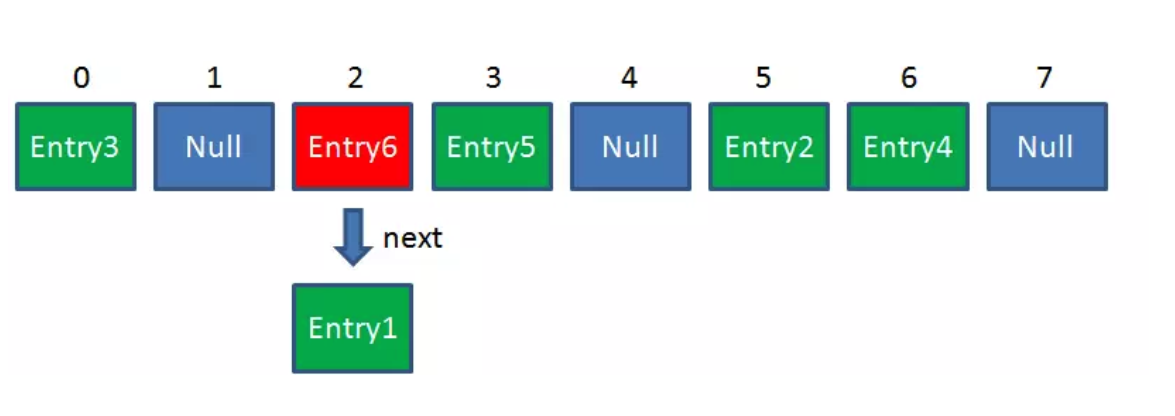
新来的Entry节点插入链表时,使用的是“头插法”。
获取元素
public V get(Object key)
使用Get方法根据Key来查找Value的时候,发生了什么呢?
首先会把输入的Key做一次Hash映射,得到对应的index:
index = Hash(“apple”);
由于刚才所说的Hash冲突,同一个位置有可能匹配到多个Entry,这时候就需要顺着对应链表的头节点,一个一个向下来查找。假设我们要查找的Key是“apple”:
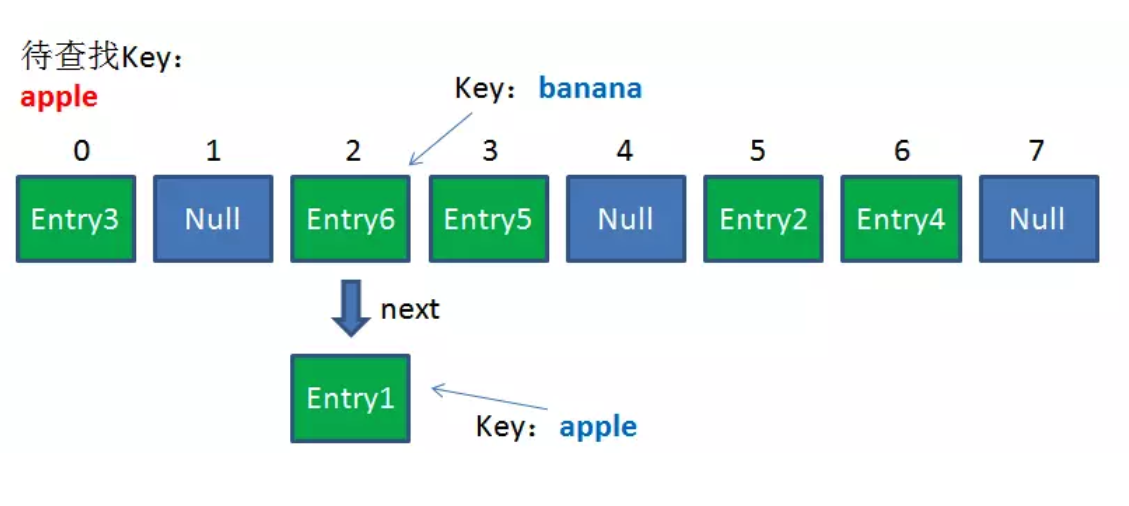
-
第一步:我们查看的是头节点Entry6,Entry6的Key是banana,显然不是我们要找的结果。
-
第二步:我们查看的是Next节点Entry1,Entry1的Key是apple,正是我们要找的结果。
之所以把Entry6放在头节点,是因为HashMap的发明者认为,后插入的Entry被查找的可能性更大。
删除元素
如果key对应的value存在,则删除这个键值对。 并返回value。如果不存在 返回null。
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
判断元素是否存在
public boolean containsKey(Object key)
存储原理
HashMap内部维护了一个用于存储元素的哈希数组,每一个数组元素都是一个 Entry 对象实例(每一个数组元素逻辑上称为一个 Bucket)。
而每个Bucket逻辑上都是一个单向链表(LinkedList),单向链表中可以存储多个Entry对象。
之所以称为逻辑上,是因为我们没有使用LinkedList类型的对象作为哈希数组的元素,而是使用Entry 对象。每个Entry 对象实例都有一个名为next的指针,指向下一个Entry 对象,从而形成单向链表(或者说,自己实现了一个简化版的LinkedList类)。
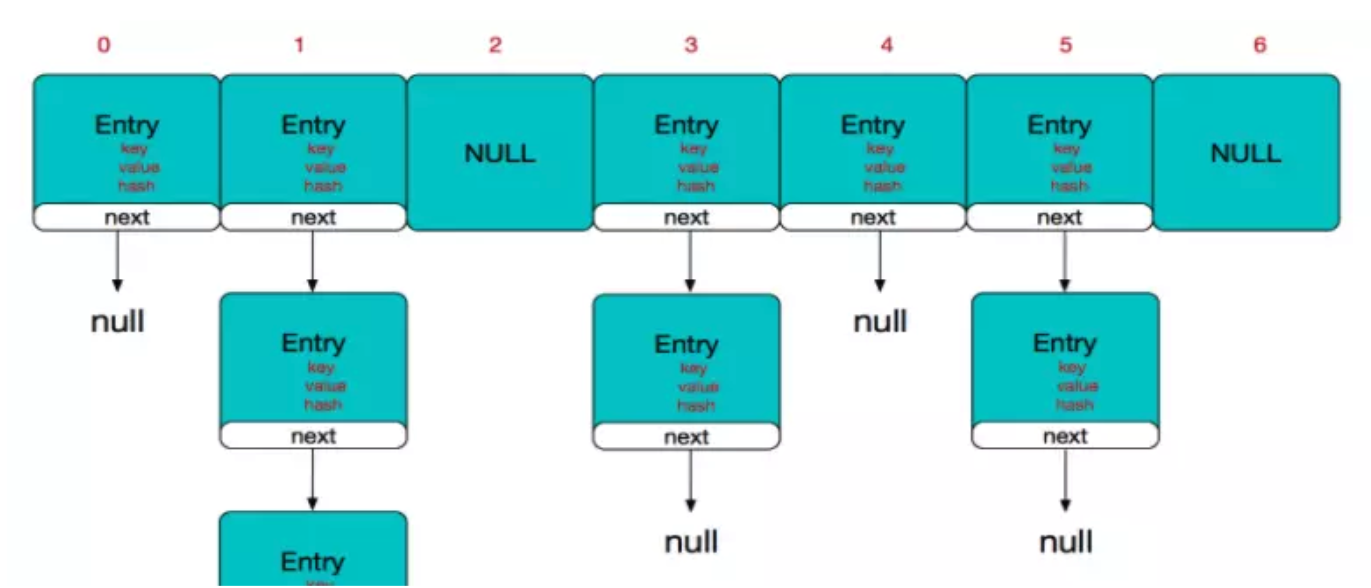
HashMap采用链表解决冲突。当准备添加一个键值对时,首先通过hash(key)方法(哈希函数,Hash Function)计算hash值,然后通过 indexFor(hash,length) 得到该待存储键值对的在这个HashMap的哈希数组中的存储位置(即哈希数组的一个索引下标)。
计算方法是先用hash&0x7FFFFFFF后,再对length取模,这就保证每一个key-value对都能存入HashMap中。
如果这个在哈希数组的这个索引下标位置,已经存放有其他键值对元素了,则将新加入的键值对元素将放在链表的头部,最早加入的键值对元素放在链表的尾部。
如上图中,左侧是一个哈希数组(存储在HashMap对象中),数组的每个元素都是一个Entry对象,同时每个对象也是一个单链表的头节点,链表是用来解决冲突的,如果不同的key映射到了哈希数组的同一位置处,就将其放入单链表中,其中新加入的元素放在链表的头部,最早加入的放在链表的尾部)。
如果定位到的数组位置不含链表(当前Entry的next指向null),那么对于查找,添加等操作很快,仅需一次寻址即可;如果定位到的数组包含链表,对于添加操作,其时间复杂度依然为O(1),因为最新的Entry会插入链表头部,仅需简单改变引用链即可,而对于查找操作来讲,此时就需要遍历链表,然后通过key对象的equals方法逐一比对查找。所以,出于性能考虑,HashMap中的链表出现越少,性能才会越好。
扩容机制
需求
HashMap的容量是有限的。当经过多次元素插入,使得HashMap达到一定饱和度时,Key映射位置发生冲突的几率会逐渐提高。
这时候,HashMap需要扩展它的长度,也就是进行扩容(Resize)。
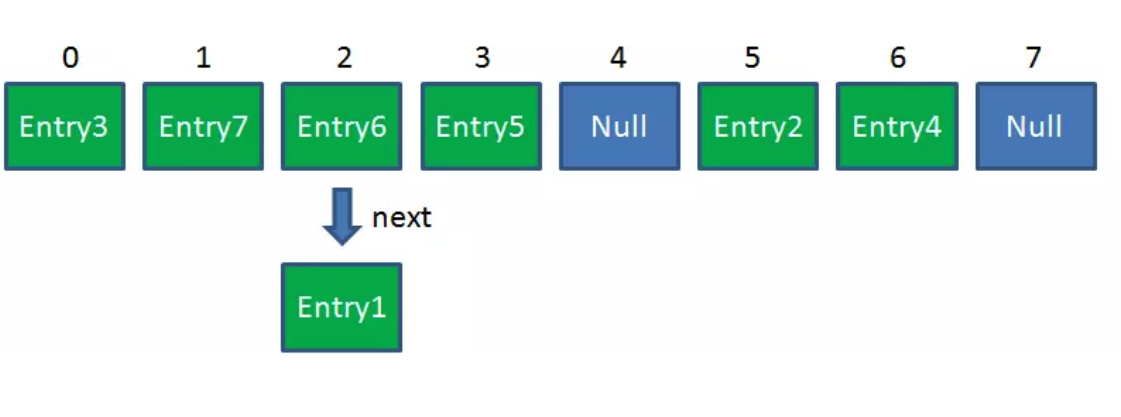
影响发生Resize的因素有三个:
- 容量(Capacity):HashMap的当前长度,是2的幂。
- 负载因子(LoadFactor):HashMap负载因子,默认值为0.75f。
- 当前HashMap中键值对(key-value)的数量(size)
衡量HashMap是否进行Resize的阈值(threshold)如下:
HashMap.Size >= Capacity * LoadFactor
负载因子(LoadFactor)
- 如果加载因子越大,对空间的利用更充分,但是查找效率会降低(链表长度会越来越长);
- 如果加载因子太小,那么表中的数据将过于稀疏(很多空间还没用,就开始扩容了),对空间造成严重浪费。
如果我们在构造方法中不指定,则系统默认加载因子为0.75,这是一个比较理想的值,一般情况下我们是无需修改的。
实现
扩容需要经历下面两个过程:
1 扩容
创建一个新的Entry空数组,长度是原数组的2倍。
2 Rehashing
遍历原Entry数组,把所有的Entry重新Hash到新数组。为什么要重新Hash呢?因为长度扩大以后,Hash的规则也随之改变。
扩容过程解析
让我们回顾一下Hash公式:
index = HashCode(Key) & (Length - 1)
当原数组长度为8时,Hash运算是和111B做与运算;新数组长度为16,Hash运算是和1111B做与运算。Hash结果显然不同。
Resize前的HashMap:
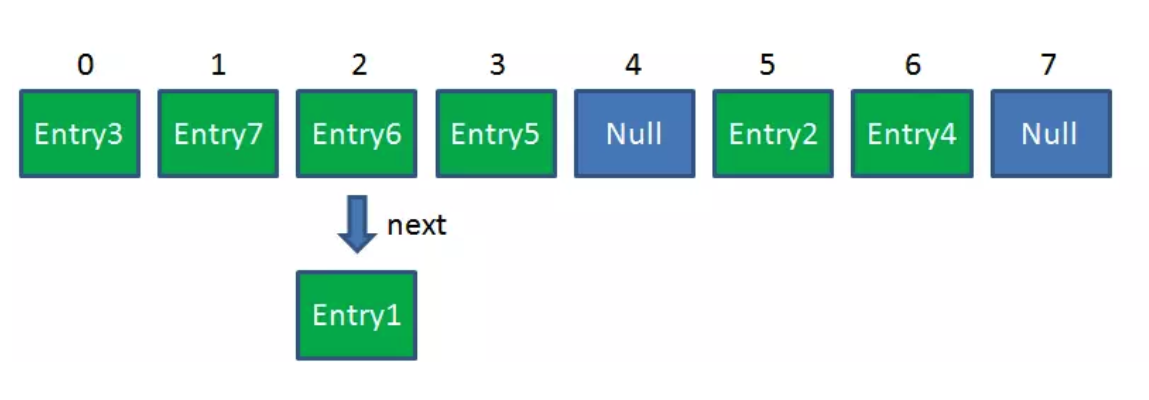
Resize后的HashMap:
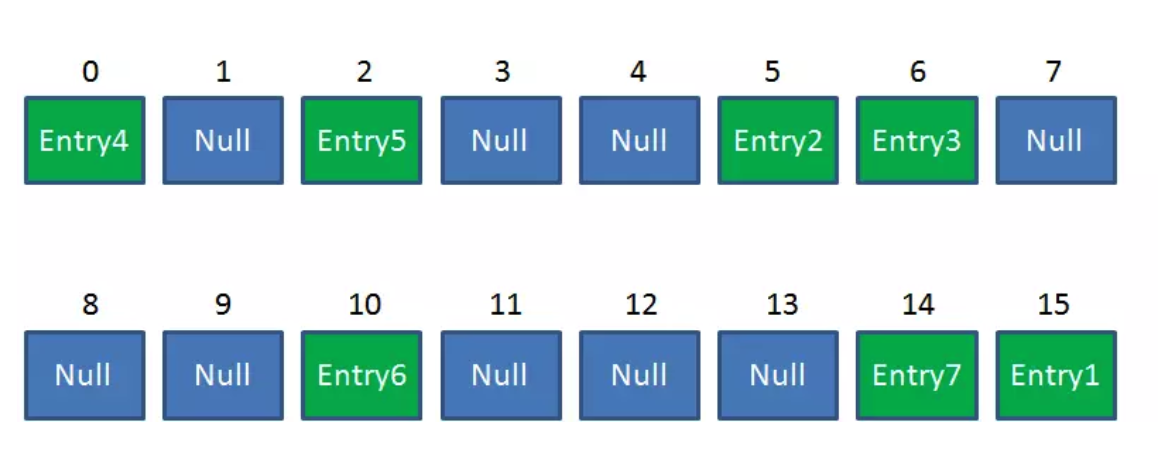
ReHash的Java代码如下:
/**
* Transfers all entries from current table to newTable.
*/
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length;
for (Entry<K,V> e : table) {
while(null != e) {
Entry<K,V> next = e.next;
if (rehash) {
e.hash = null == e.key ? 0 : hash(e.key);
}
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
}
}
}
JDK 1.8 后的改进
在JDK1.8 对HashMap做了改造,如下图:
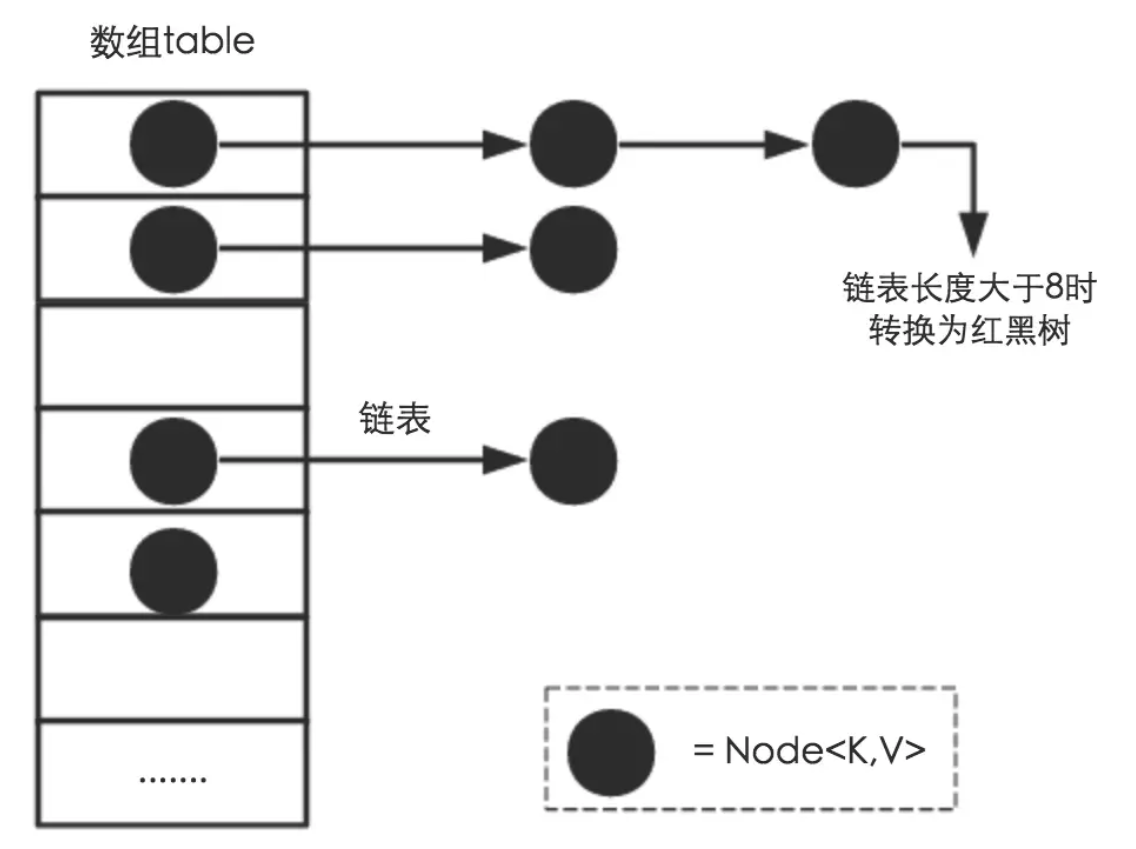
JDK 1.8 以前 HashMap 的实现是 数组+链表,即使哈希函数取得再好,也很难达到元素百分百均匀分布。
当 HashMap 中有大量的元素都存放到同一个Bucket 中时,这个Bucket下有一条长长的链表,这个时候 HashMap 就相当于一个单链表,假如单链表有 n 个元素,遍历的时间复杂度就是 O(n),完全失去了它的优势。
针对这种情况,JDK 1.8 中引入了红黑树(查找时间复杂度为 $O(log_2n))$ 来优化这个问题。
Reference
- 漫画:什么是HashMap? - https://juejin.im/post/5a215783f265da431d3c7bba
- 漫画:高并发下的HashMap - https://juejin.im/post/5a224e1551882535c56cb940
- 图解HashMap(一) - https://juejin.im/post/5a23f82ff265da432003109b