判断一个元素是否存在一个集合中
先来看几个比较常见的例子
- 字处理软件中,需要检查一个英语单词是否拼写正确
- 在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上
- 在网络爬虫里,一个网址是否被访问过
- yahoo, gmail等邮箱垃圾邮件过滤功能
这几个例子有一个共同的特点: 如何判断一个元素是否存在一个集合中?
常规思路:
- 数组
- 链表
- 树、平衡二叉树、Trie
- HashMap (红黑树):通过将值映射到 HashMap 中,就可以在 O(1) 的时间复杂度内返回结果(判断这个元素是否在集合中),效率奇高。但是 HashMap 的实现也有缺点,例如存储容量占比高,考虑到负载因子的存在,通常空间是不能被用满的,而一旦你的值很多例如上亿的时候,那 HashMap 占据的内存大小就变得很可观了。
- 哈希表
虽然上面描述的这几种数据结构配合常见的排序、二分搜索可以快速高效的处理绝大部分判断元素是否存在集合中的需求。
但是当集合里面的元素数量足够大,如果有500万条记录甚至1亿条记录呢?这个时候常规的数据结构的问题就凸显出来了。
数组、链表、树等数据结构会存储元素的内容,一旦数据量过大,消耗的内存也会呈现线性增长,最终达到瓶颈。
有的同学可能会问,哈希表不是效率很高吗?查询效率可以达到O(1)。但是哈希表需要消耗的内存依然很高。使用哈希表存储一亿个垃圾 email 地址的消耗?
哈希表的做法:首先,哈希函数将一个email地址映射成8字节信息指纹;考虑到哈希表存储效率通常小于50%(哈希冲突);因此消耗的内存:8 * 2 * 1亿 字节 = 1.6G 内存,普通计算机是无法提供如此大的内存。这个时候,布隆过滤器(Bloom Filter)就应运而生。在继续介绍布隆过滤器的原理时,先讲解下关于哈希函数的预备知识。
什么是 Bloom Filter
Bloom Filter,被译作称布隆过滤器,是一种空间效率很高的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在于特定集合中”。
Bloom filter 可以看做是对 bit-map 的扩展,它的原理是:
当一个元素被加入集合时,通过 K 个 Hash 函数将这个元素映射成一个位阵列(Bit array) 中的 K 个点,且把这些点的值置为 1。
当需要判断这个元素是否存在在集合时,将这个元素分别再放到这 K 个 Hash 函数中,我们只要看看此时分别映射到的这 K 个点是不是都是 1,就(大约) 知道这个元素是否存在于集合中了:
- 如果这些点有任何一个点的值为 0,则被检索元素一定不在于集合中;
- 如果所有这些点的值都是 1,则被检索元素很可能存在于集合中。
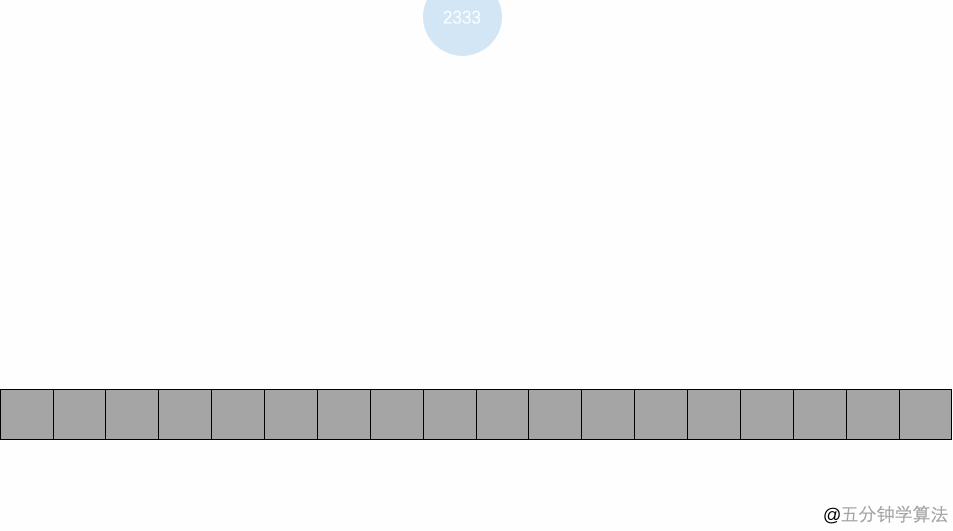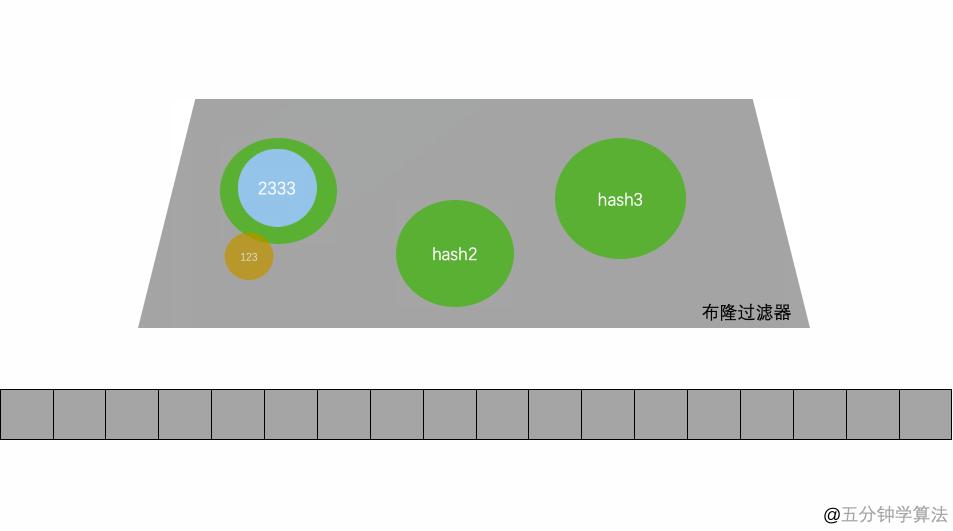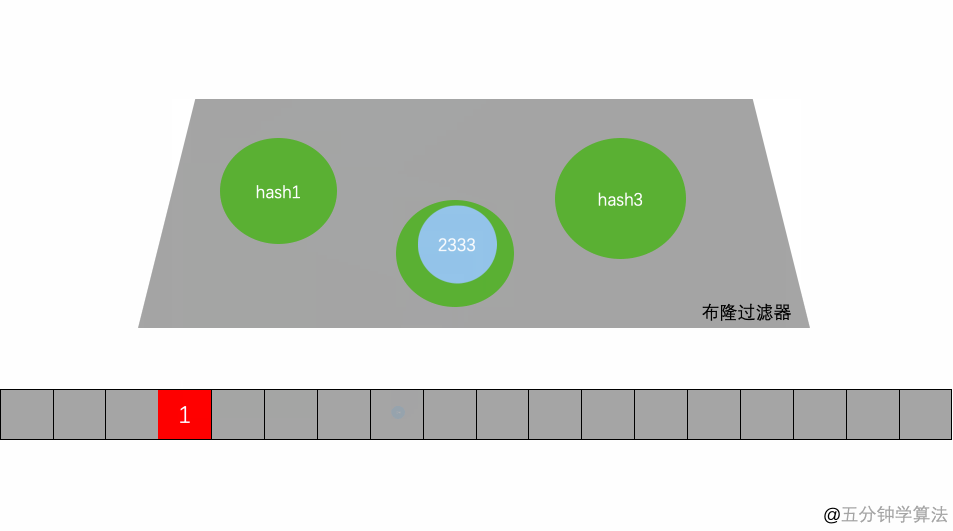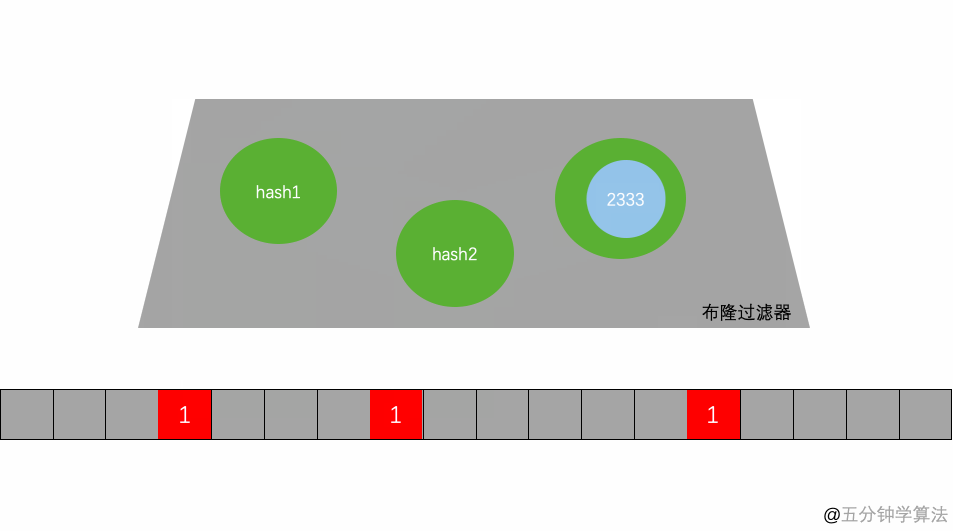
但 Bloom Filter 的这种高效是有一定代价的:在判断一个元素是否属于某个集合时,有可能会把不属于这个集合的元素误认为属于这个集合(false positive)。因此,Bloom Filter 不适合那些“零 错误”的应用场合。而在能容忍低错误率的应用场合下,Bloom Filter 通过极少的错误换取了存储空间的极大节省。
...