跳跃表(跳表,Skiplist)
引言
Redis因为其完全基于内存、性能出色,加上具备丰富的数据类型,在电商环境中深受后端开发的喜爱。其中有序集合zset就是基本数据类型之一,并且每个member都带有score(可用于排序),因此很适合在打赏日榜、近一周收益这类场景中运用。
定义
跳表这种数据结构是由 William Pugh 发明的,关于跳表的详细介绍可以参考论文:「Skip Lists: A Probabilistic Alternative to Balanced Trees」,论文中详细阐述了关于 skiplist 查找元素、删除元素、插入元素的算法伪代码,以及时间复杂度的分析
跳表(SkipList):跳表全称叫做跳跃表,简称跳表。跳表是一个随机化的数据结构,实质是一种可以进行二分查找的有序链表。跳表在原有的有序链表上增加了多级索引,通过索引来实现快速查询。跳表不仅能提高搜索性能,同时也可以提高插入和删除操作的性能。
跳表是一个随机化的数据结构,可以被看做二叉树的一个变种,它在性能上和红黑树、AVL树不相上下,但是跳表的原理非常简单,目前在Redis和LevelDB中都有用到。
思想
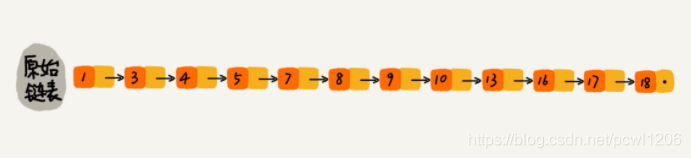
对于一个单链表来说,即使链表中的数据是有序的,如果我们想要查找某个数据,也必须从头到尾的遍历链表,很显然这种查找效率是十分低效的,时间复杂度为O(n)。
那么我们如何提高查找效率呢?我们可以对链表建立一级“索引”,每两个结点提取一个结点到上一级,我们把抽取出来的那一级叫做索引或者索引层,如下图所示,down表示down指针。
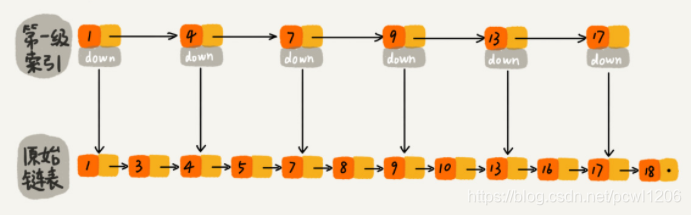
假设我们现在要查找值为16的这个结点。我们可以先在索引层遍历,当遍历索引层中值为13的时候,通过值为13的结点的指针域发现下一个结点值为17,因为链表本身有序,所以值为16的结点肯定在13和17这两个结点之间。然后我们通过索引层结点的down指针,下降到原始链表这一层,继续往后遍历查找。这个时候我们只需要遍历2个结点(值为13和16的结点),就可以找到值等于16的这个结点了。如果使用原来的链表方式进行查找值为16的结点,则需要遍历10个结点才能找到,而现在只需要遍历7个结点即可,从而提高了查找效率。
那么我们可以由此得到启发,和上面建立第一级索引的方式相似,在第一级索引的基础上,每两个一级索引结点就抽到一个结点到第二级索引中。再来查找值为16的结点,只需要遍历6个结点即可,从而进一步提高了查找效率。
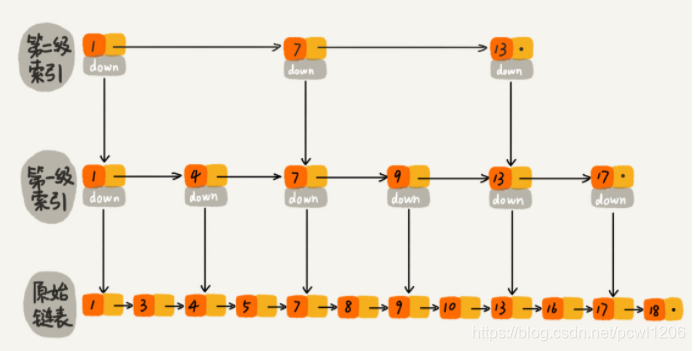
上面举得例子中的数据量不大,所以即便加了两级索引,查找的效率提升的也不是很明显,下面通过一个64结点的链表来更加直观的感受下索引提升查找效率,如图所示,建立了五级索引。
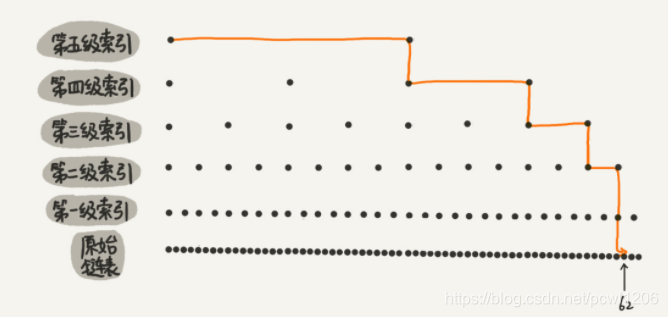
从图中我们可以看出来,原来没有索引的时候,查找62需要遍历62个结点,现在只需要遍历11个结点即可,速度提高了很多。那么,如果当链表的长度为10000、10000000时,通过构件索引之后,查找的效率就会提升的非常明显。
复杂度
| Operation | Average | Worst case |
|---|---|---|
| Search | θ(logn) | O(n) |
| Insert | θ(logn) | O(n) |
| Delete | θ(logn) | O(n) |
操作
查询
从跳表的当前的最大层数 level 层开始查找,在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点,然后移动至下一层进行查找,重复这个过程直至到达第 1 层。此时,若第 1 层的下一个节点的值等于 target,则返回 true;反之,则返回 false。
比如要查询 23 ,如图所示:
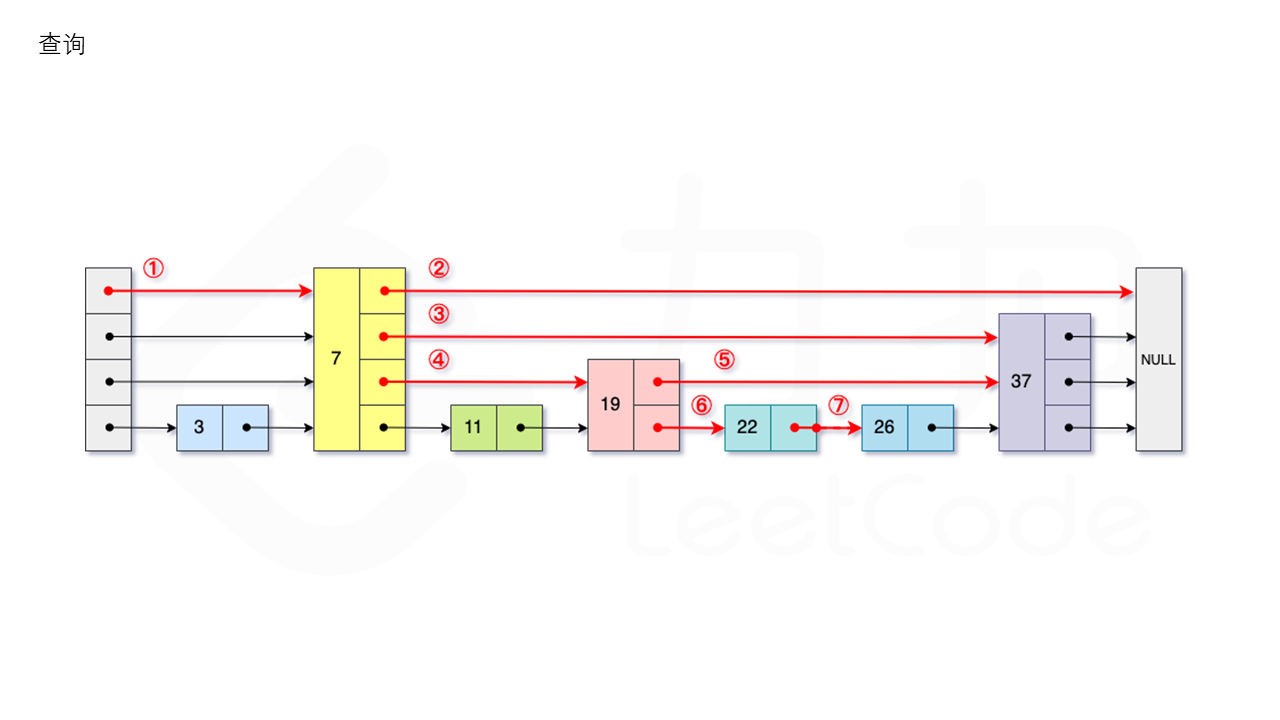
插入
跳表插入的时间复杂度为:O(logn),支持高效的动态插入。
在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是O(1)。但是为了保证原始链表中数据的有序性,我们需要先找到要插入的位置,这个查找的操作就会比较耗时。
对于纯粹的单链表,需要遍历每个结点,来找到插入的位置。但是对于跳表来说,查找的时间复杂度为O(logn),所以这里查找某个数据应该插入的位置的时间复杂度也是O(logn)。
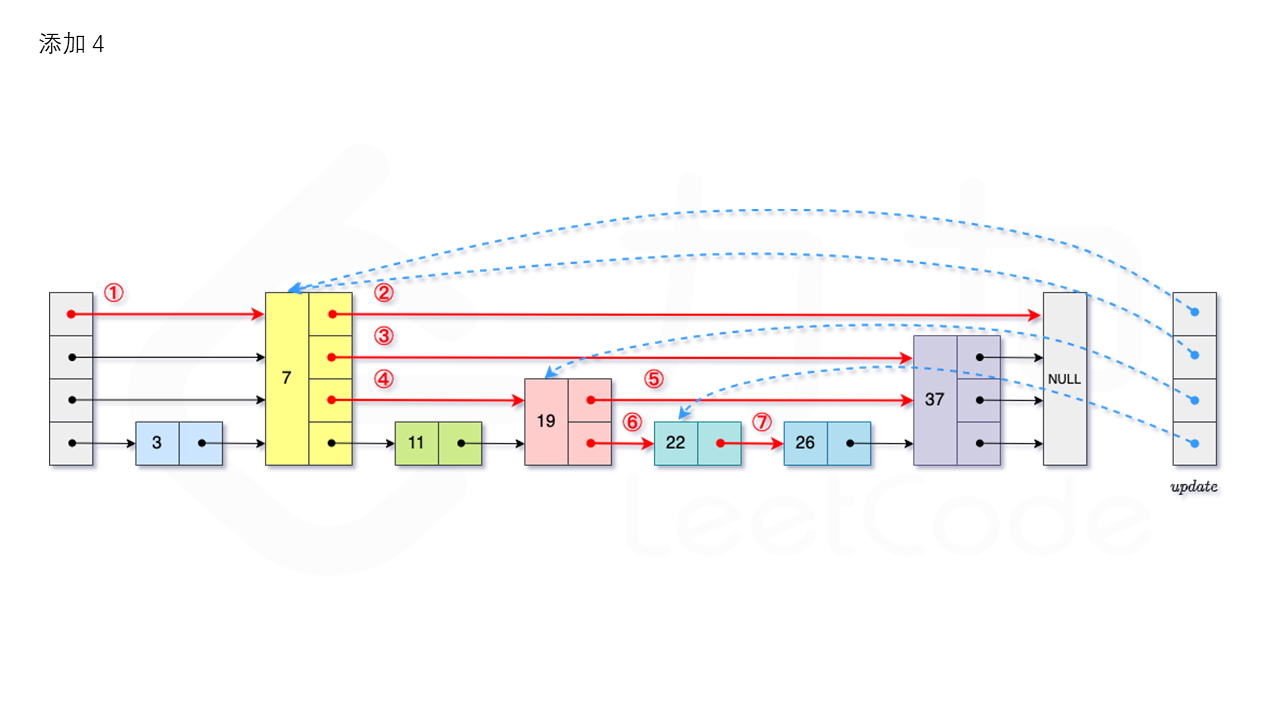
从跳表的当前的最大层数 level 层开始查找,在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点,然后移动至下一层进行查找,重复这个过程直至到达第 1 层。设新加入的节点为 newNode,我们需要计算出(随机决定)此节点的“层高” lv,如果 level 小于 lv,则同时需要更新 level。我们用数组 update 保存每一层插入点的“前驱节点”,第 i 层最后的节点为 update[i]。我们将 newNode 的后续节点指向 update[i] 的下一个节点,同时更新 update[i] 的后续节点为 newNode。
比如要插入 23,如图所示:
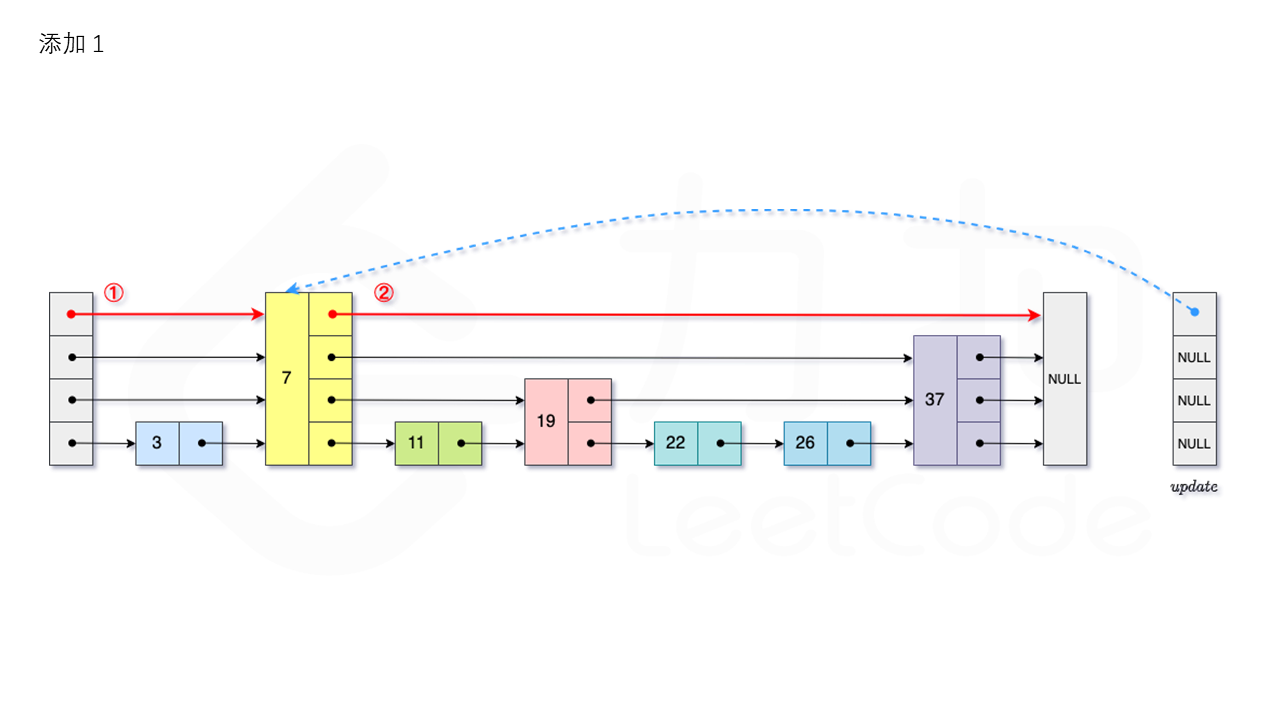
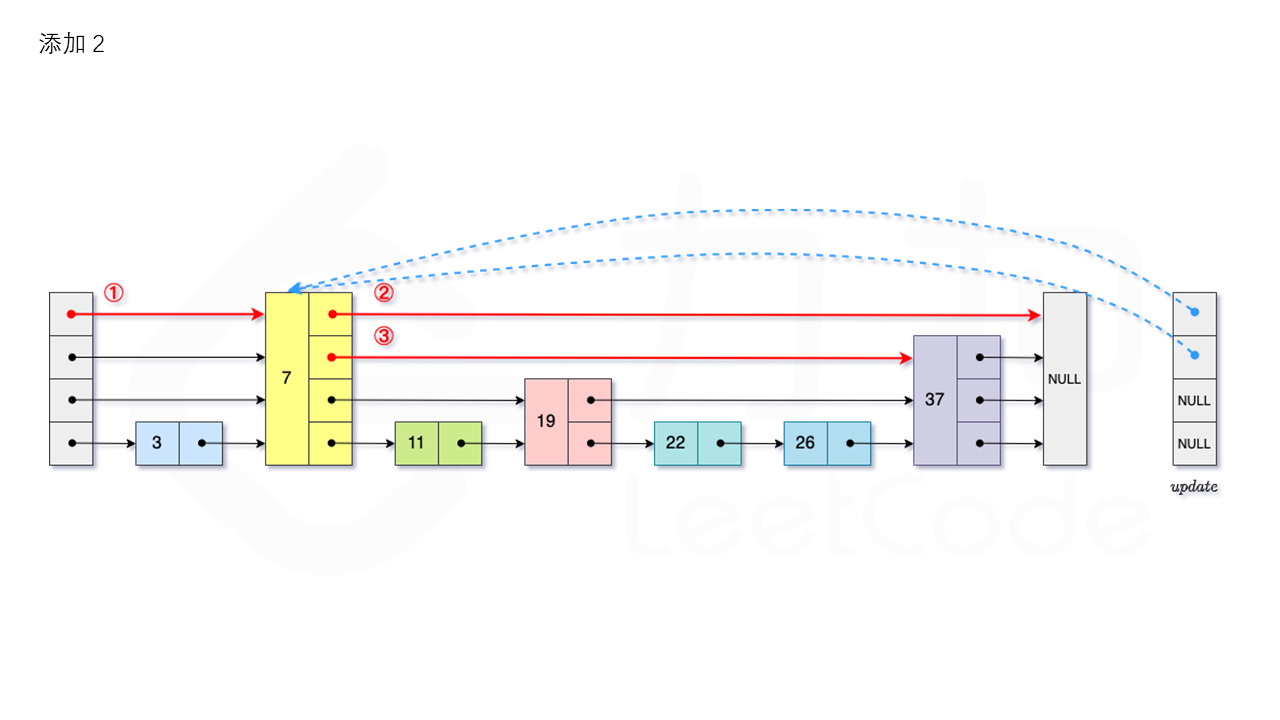
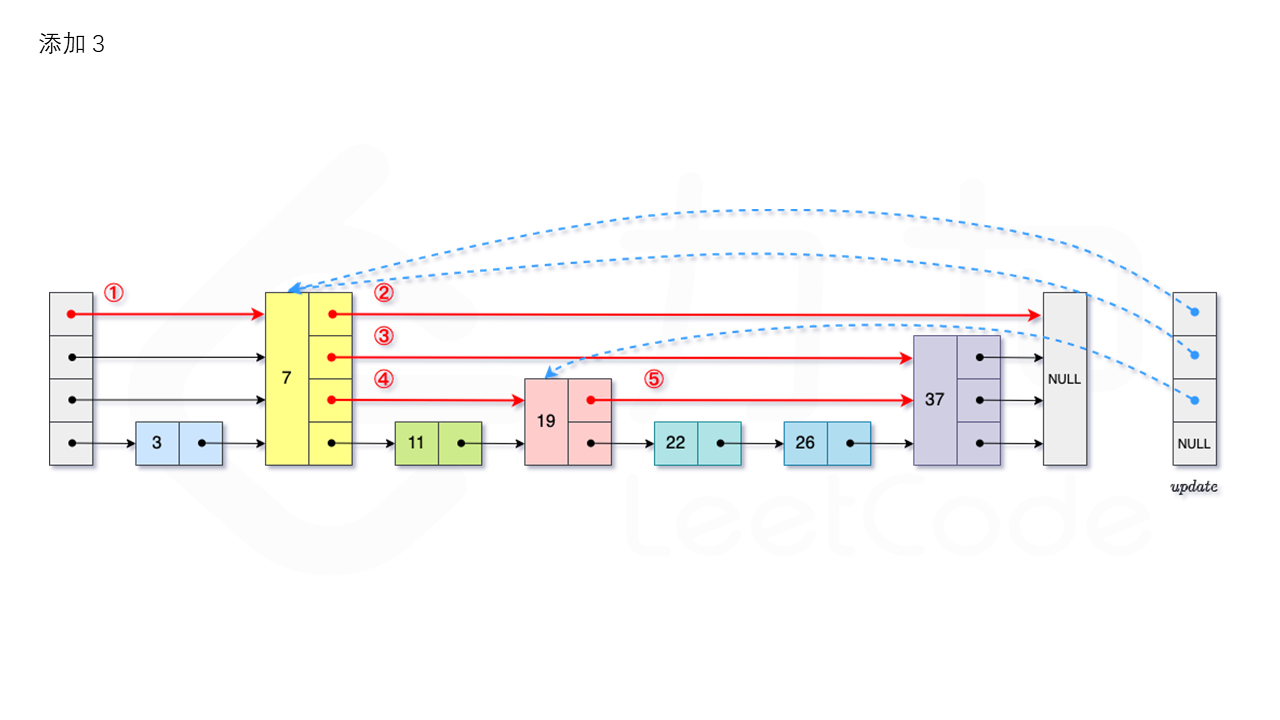
删除
跳表的删除操作的平均时间复杂度为:O(logn),支持动态的删除。
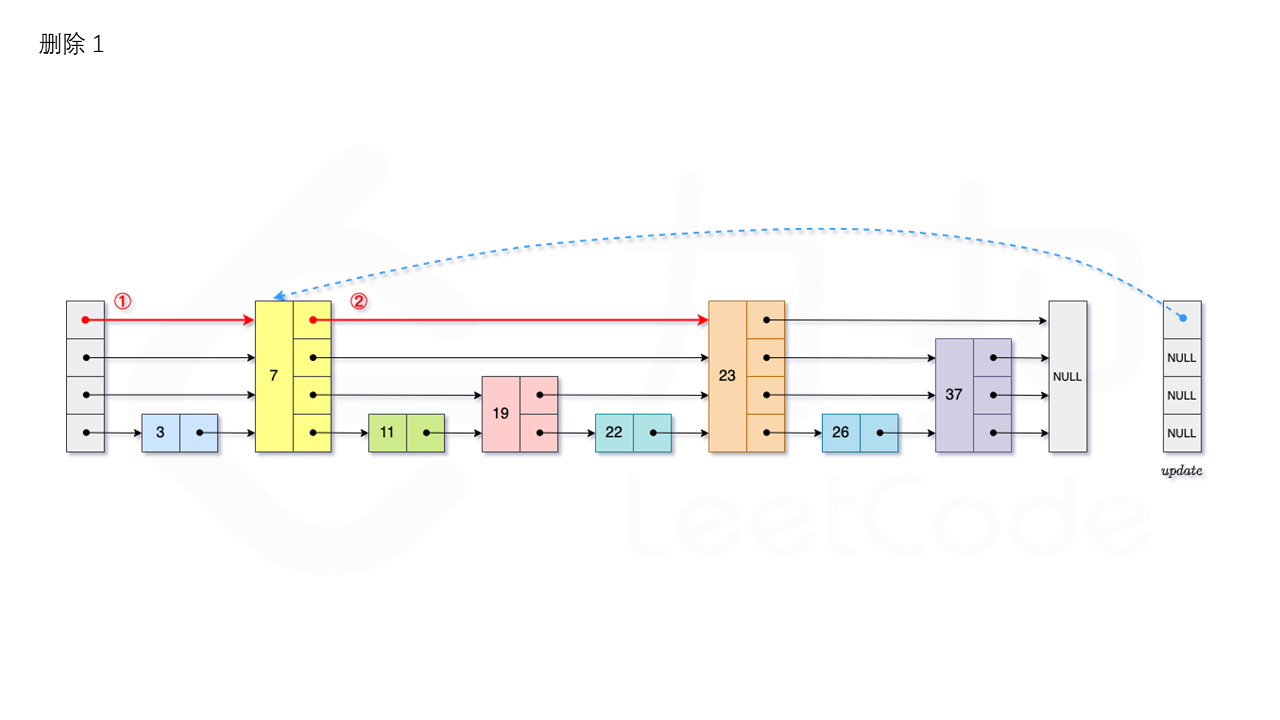
首先我们需要查找当前元素是否存在跳表中。从跳表的当前的最大层数 level 层开始查找,在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点,然后移动至下一层进行查找,重复这个过程直至到达第 1 层。
如果第 1 层的下一个节点不等于 num 时,则表示当前元素不存在直接返回。
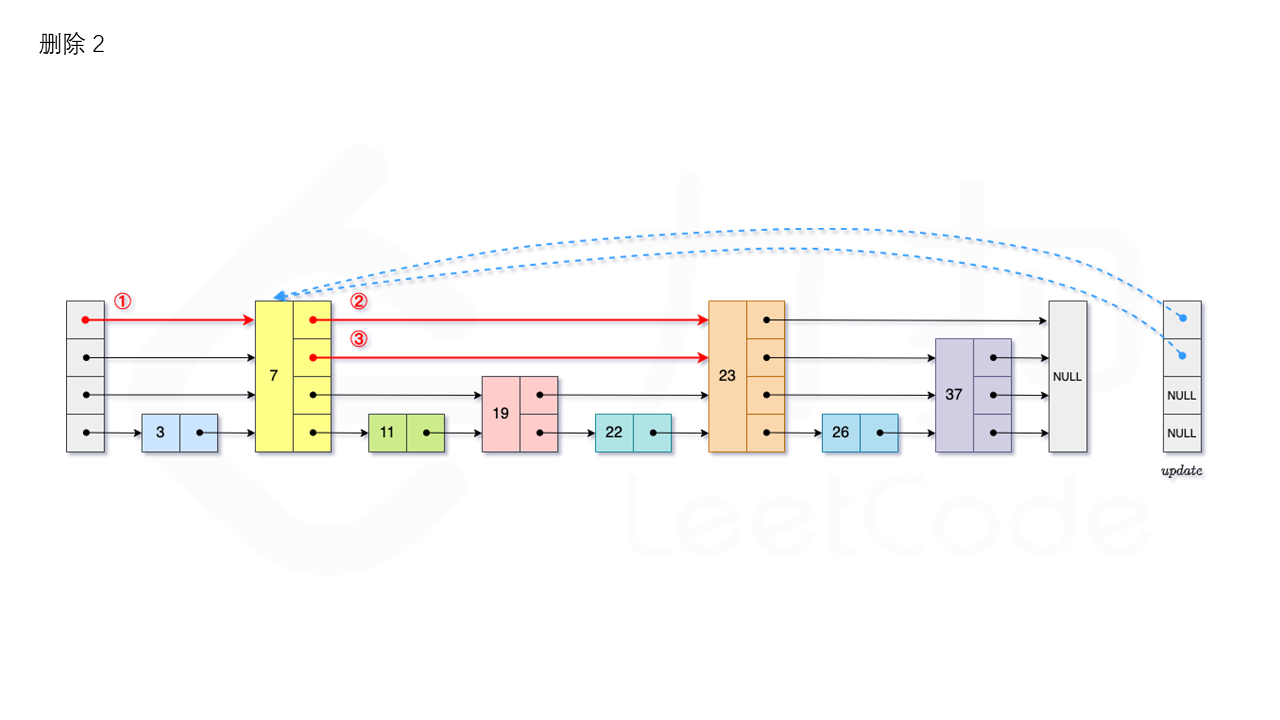
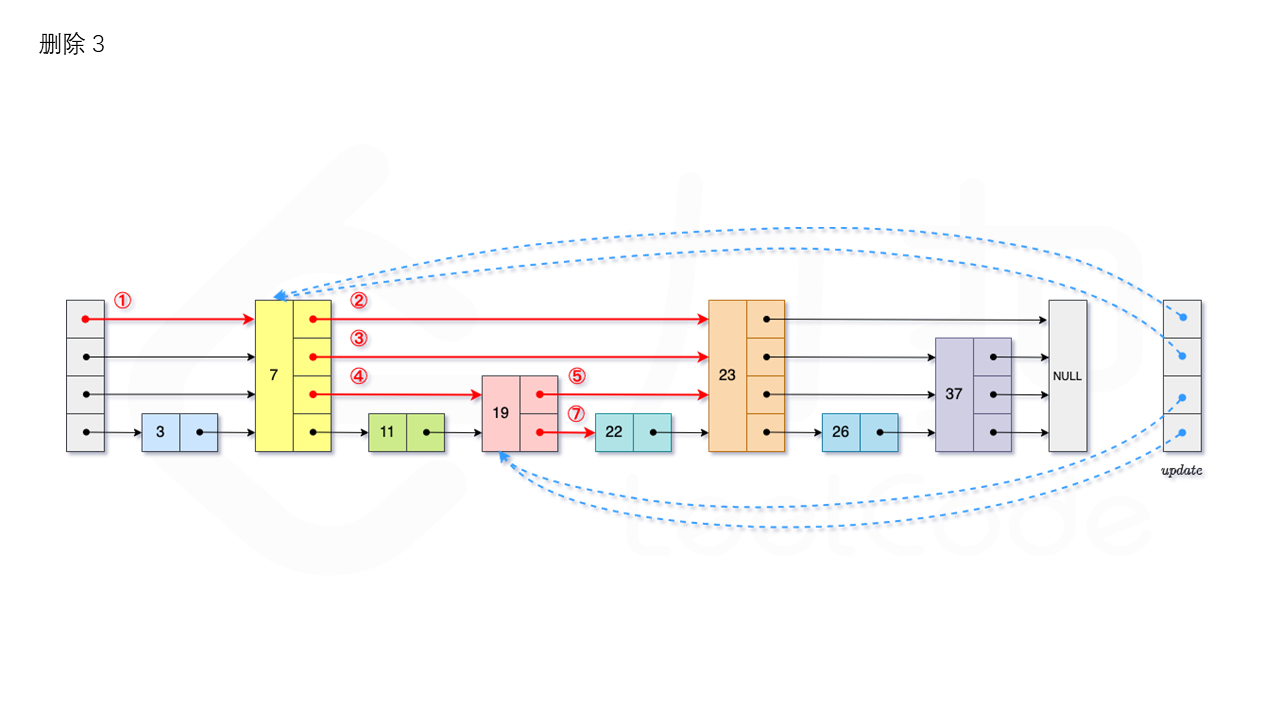
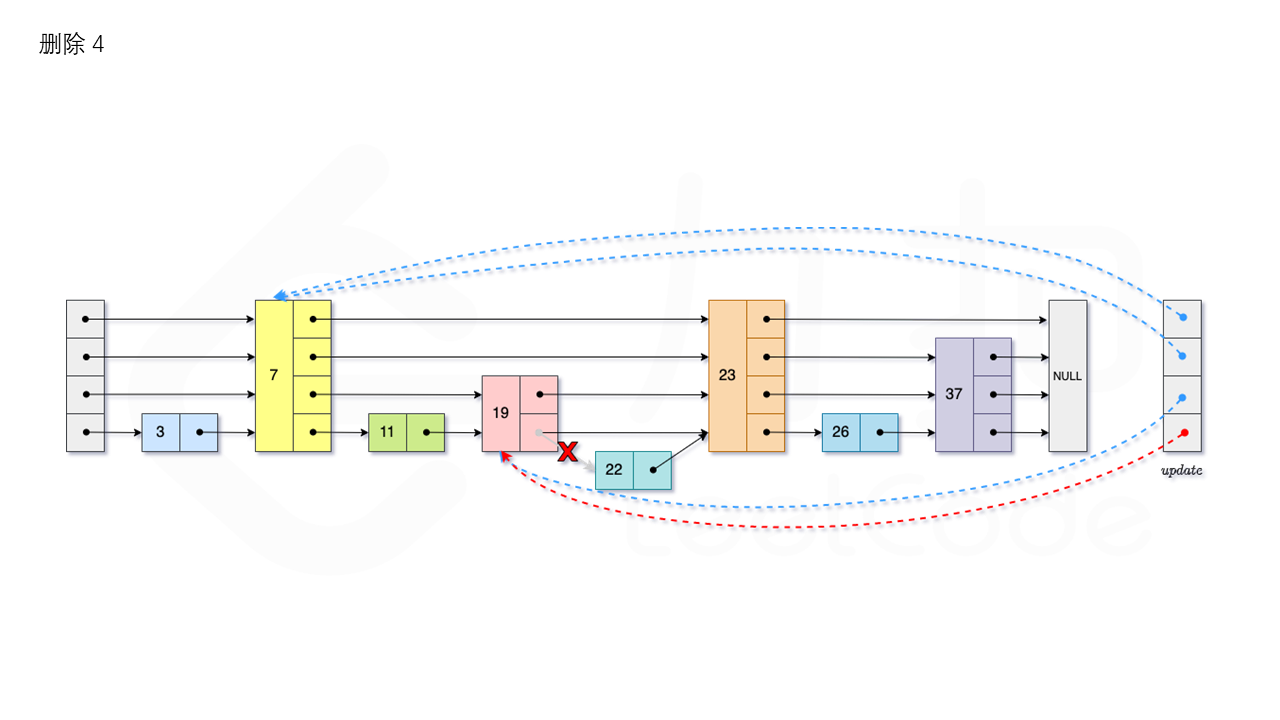
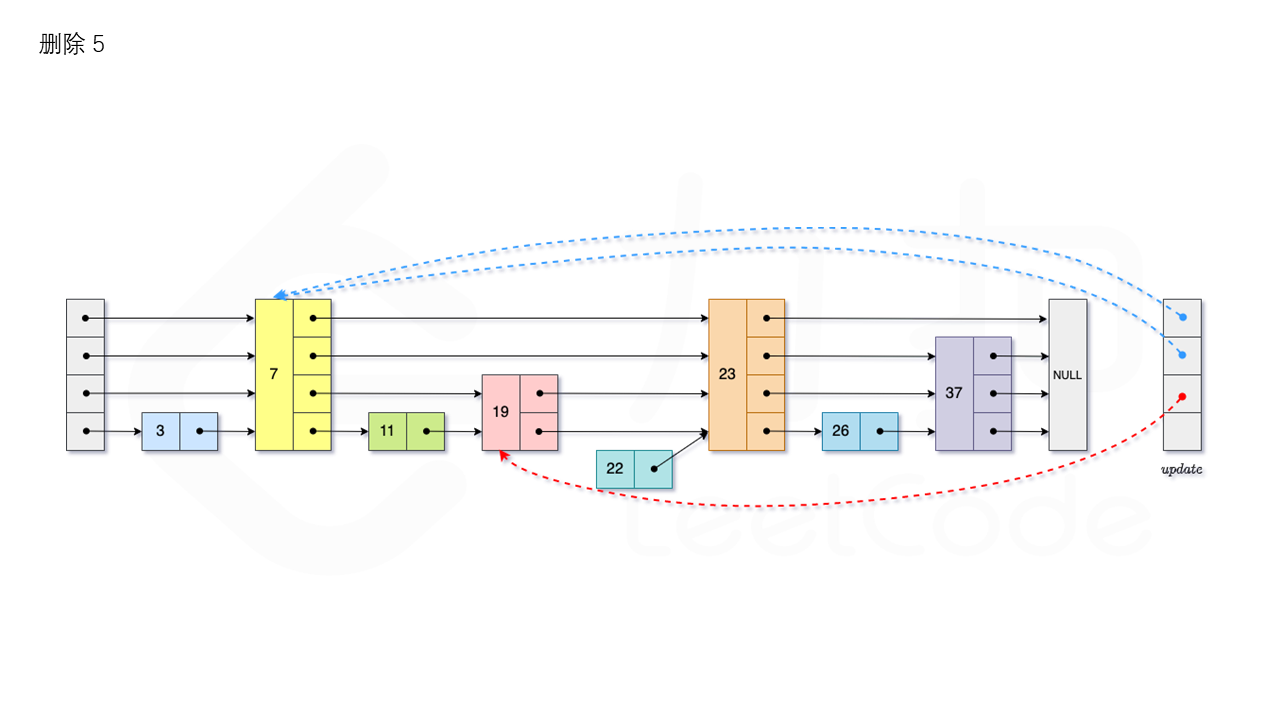
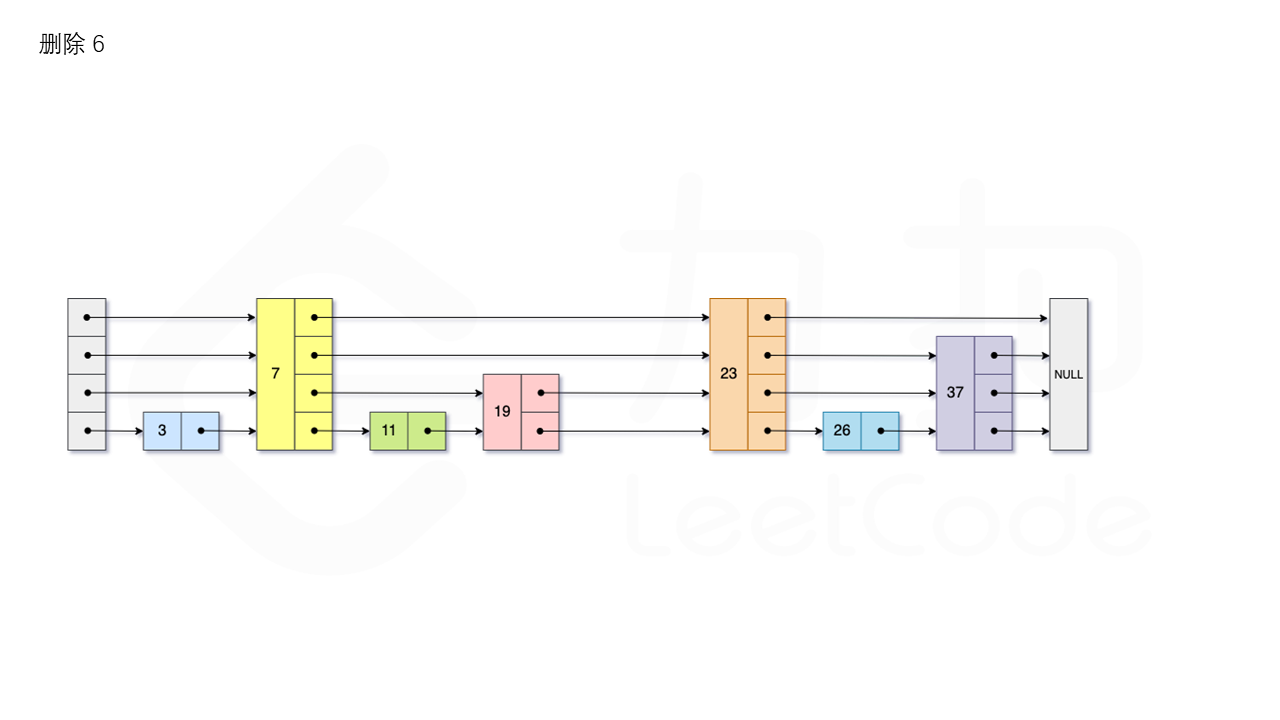
我们用数组 update 保存每一层查找的最后一个节点,第 i 层最后的节点为 update[i]。此时如果第 i 层的下一个节点的值为 num,则我们需要将其从跳表中将其删除。由于第 i 层的以 p 的概率出现在第 i+1 层,因此我们应当从第 1 层开始往上进行更新,将 num 从 update[i] 的下一跳中删除,同时更新 update[i] 的后续节点,直到当前层的链表中没有出现 num 的节点为止。
最后我们还需要更新跳表中当前的最大层数 level。
比如删除 22,如图所示:
索引动态更新
当我们不断地往跳表中插入数据时,我们如果不更新索引,就有可能出现某2个索引节点之间的数据非常多的情况,在极端情况下,跳表还会退化成单链表,如下图所示:
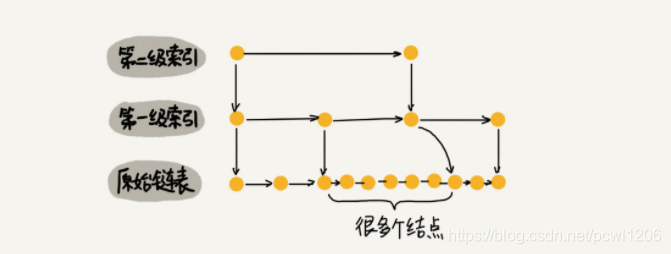
作为一种动态数据结构,我们需要某种手段来维护索引与原始链表大小之间的平衡,也就是说,如果链表中的结点多了,索引结点就相应地增加一些,避免复杂度退化,以及查找、插入和删除操作性能的下降。
如果你了解红黑树、AVL树这样的平衡二叉树,你就会知道它们是通过左右旋的方式保持左右子树的大小平衡,而跳表是通过随机函数来维护“平衡性”。
当我们往跳表中插入数据的时候,我们可以通过一个随机函数,来决定这个结点插入到哪几级索引层中(相当于随机决定该节点的“层高”),比如随机函数生成了值K,那我们就将这个结点添加到第一层到第K层这K层索引中。如下图中要插入数据为6,K=2的例子:
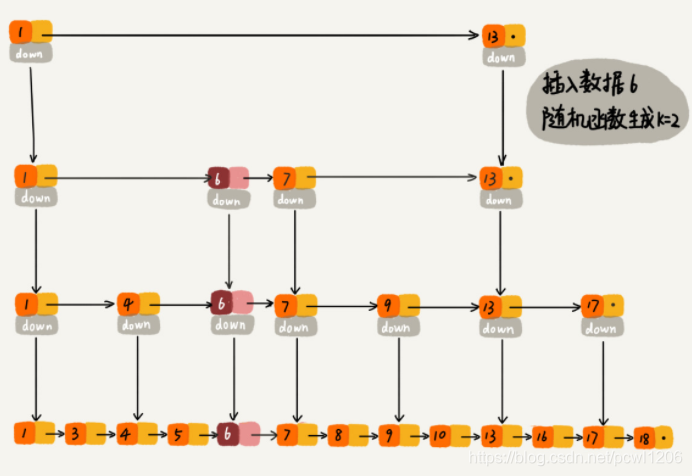
随机函数的选择是非常有讲究的,从概率上讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能的过度退化。
实现
Golang
package main
import (
"fmt"
"math/rand"
"time"
)
const (
MaxLevel int = 16 // 跳表最大层数
Probability float64 = 0.5 // 每一层存在的概率(用于随机层数)
)
// 节点结构
type Node struct {
value int // 节点存储的值
next []*Node // 每层对应的下一个节点指针数组
}
// 跳表结构
type SkipList struct {
head *Node // 头节点(dummy head)
level int // 当前跳表的最大层数(从 0 开始)
}
// 创建一个新的节点
func newNode(value int, level int) *Node {
return &Node{
value: value,
next: make([]*Node, level),
}
}
// 创建一个新的跳表
func NewSkipList() *SkipList {
// 初始化时,头节点为空值,最大层
return &SkipList{
head: newNode(0, MaxLevel),
level: 0,
}
}
// 随机生成一个层高(用于插入时的层高),最小为 1,最大为 MaxLevel
// 类似于“扔硬币”:层数越高,概率越低。
func randomLevel() int {
level := 1
for rand.Float64() < Probability && level < MaxLevel {
level++
}
return level
}
// 查找值是否存在
func (sl *SkipList) Search(value int) bool {
curr := sl.head
// 从最高层(包含节点数量最少的层)开始向下搜索
for i := sl.level - 1; i >= 0; i-- {
// 假设我们有以下跳表结构,共 3 层:
// Level 2: 1 -----------> 9
// Level 1: 1 ---> 3 ---> 9
// Level 0: 1 -> 2 -> 3 -> 4 -> 9
// 此时,节点 1 出现在三层中,所以它需要有 next[0], next[1], next[2] 三个指针:
// node1.next[0] -> node2 // 在 level 0 指向下一个是 2
// node1.next[1] -> node3 // 在 level 1 指向下一个是 3
// node1.next[2] -> node9 // 在 level 2 指向下一个是 9
// 所以,next[i] 表示“第 i 层链表中当前节点的下一个节点”。
// 向右找(下一个节点),直到找不到比目标小的值
for curr.next[i] != nil && curr.next[i].value < value {
curr = curr.next[i]
}
}
curr = curr.next[0]
// 检测当前元素的值是否等于 value
return curr != nil && curr.value == value
}
// 插入一个值
func (sl *SkipList) Insert(value int) {
update := make([]*Node, MaxLevel) // 记录在每一层中新节点要插入的位置之前的那个节点。
curr := sl.head
// 找到需要更新的位置(每一层向右找)- 从跳表的当前的最大层(sl.level - 1)开始查找,在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点,然后移动至下一层进行查找,重复这个过程直至到达最底层(0)
for i := sl.level - 1; i >= 0; i-- {
for curr.next[i] != nil && curr.next[i].value < value {
curr = curr.next[i]
}
// 把当前这个节点 curr 记录到 update[i],表示该层插入点的“前驱节点”。
update[i] = curr
}
// 如果底层节点已存在该值,跳表不允许重复值,所以直接返回。
if curr.next[0] != nil && curr.next[0].value == value {
return
}
// 随机决定新节点的"层高"
newLevel := randomLevel()
// 如果新节点层数比当前跳表高,就将高出部分的 update[i] 设置成头节点
if newLevel > sl.level {
for i := sl.level; i < newLevel; i++ {
update[i] = sl.head
}
sl.level = newLevel
}
// 创建并插入新节点
n := newNode(value, newLevel)
for i := 0; i < newLevel; i++ {
// 在每一层:将 update[i] 原本指向的节点链接到 newNode.next[i];
// 然后 update[i].next[i] = newNode,将新节点链接上去。
// 形象点说:像往链表中间插入一个新节点,只不过你在多层链表中都做了这件事。
n.next[i] = update[i].next[i]
update[i].next[i] = n
}
}
// 删除一个值
func (sl *SkipList) Delete(value int) {
update := make([]*Node, MaxLevel)
curr := sl.head
// 查找“每一层删除点的前驱节点”
for i := sl.level - 1; i >= 0; i-- {
for curr.next[i] != nil && curr.next[i].value < value {
curr = curr.next[i]
}
update[i] = curr // update[i] 记录了第 i 层中待删节点的前驱节点。
}
target := curr.next[0]
// 从底层第 0 层开始确认是否是我们要删的节点;
// 如果不存在或值不匹配,则提前退出。
if target == nil || target.value != value {
return
}
// 删除每层中的节点
// 依次遍历每一层,如果该层确实连接着 target 节点,就将它跳过去(断链);
// 也就是说,让 update[i].next[i] 直接指向 target.next[i],忽略中间的节点。
for i := 0; i < sl.level; i++ {
if update[i].next[i] != target {
continue
}
update[i].next[i] = target.next[i]
}
// 如果最高层没有节点了,降低跳表层级
// 如果最上层的链表已经变空(即 head.next[i] == nil),说明该层无用,跳表可以降低高度;
// 这一步确保跳表结构不会“徒有空层”,节省空间,也避免浪费查找时间。
for sl.level > 0 && sl.head.next[sl.level-1] == nil {
sl.level--
}
}
// 打印跳表(调试用)
func (sl *SkipList) Print() {
fmt.Println("SkipList:")
for i := sl.level - 1; i >= 0; i-- {
curr := sl.head.next[i]
fmt.Printf("Level %d: ", i)
for curr != nil {
fmt.Printf("%d ", curr.value)
curr = curr.next[i]
}
fmt.Println()
}
}
func main() {
rand.Seed(time.Now().UnixNano())
sl := NewSkipList()
sl.Insert(3)
sl.Insert(6)
sl.Insert(7)
sl.Insert(9)
sl.Insert(12)
sl.Insert(19)
sl.Insert(17)
sl.Insert(26)
sl.Print()
//fmt.Println("Search 19:", sl.Search(19))
//fmt.Println("Search 5:", sl.Search(5))
//
//sl.Delete(17)
//sl.Delete(3)
//fmt.Println("After deletion:")
//sl.Print()
}
zset底层存储结构
zset 底层的存储结构包括ziplist或skiplist,在同时满足以下两个条件的时候使用ziplist,其他时候使用skiplist,两个条件如下:
- 有序集合保存的元素数量小于128个
- 有序集合保存的所有元素的长度小于64字节
当ziplist作为zset的底层存储结构时候,每个集合元素使用两个紧挨在一起的压缩列表节点来保存,第一个节点保存元素的成员,第二个元素保存元素的分值。
当skiplist作为zset的底层存储结构的时候,使用skiplist按序保存元素及分值,使用dict来保存元素和分值的映射关系。
ziplist数据结构
ziplist作为zset的存储结构时,格式如下图,细节就不多说了,我估计大家都看得懂,紧挨着的是元素memeber和分值socore,整体数据是有序格式。


skiplist数据结构
skiplist作为zset的存储结构,整体存储结构如下图,核心点主要是包括一个dict对象和一个skiplist对象。dict保存key/value,key为元素,value为分值;skiplist保存的有序的元素列表,每个元素包括元素和分值。两种数据结构下的元素指向相同的位置。
Zset应用场景
Redis 的 Zset(有序集合)类型在许多场景中都非常有用,以下是一些常见的应用场景:
- 排行榜:Zset 非常适合用于实现各种排行榜。例如,你可以将用户的 ID 作为元素,用户的分数作为分数,然后使用 Zset 来存储和排序所有用户的分数。你可以很容易地获取到分数最高的用户,或者获取到任何用户的排名。
- 时间线:你可以使用 Zset 来实现时间线功能。例如,你可以将发布的消息作为元素,消息的发布时间作为分数,然后使用 Zset 来存储和排序所有的消息。你可以很容易地获取到最新的消息,或者获取到任何时间段内的消息。
- 带权重的队列:Zset 可以用于实现带权重的队列。例如,你可以将任务作为元素,任务的优先级作为分数,然后使用 Zset 来存储和排序所有的任务。你可以很容易地获取到优先级最高的任务,或者按优先级顺序执行任务。
- 延时队列:你可以将需要延时处理的任务作为元素,任务的执行时间作为分数,然后使用 Zset 来存储和排序所有的任务。你可以定期扫描 Zset,处理已经到达执行时间的任务。